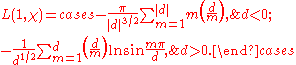Class number formula
Encyclopedia
In number theory
, the class number formula relates many important invariants of a number field to a special value of its Dedekind zeta function
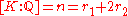 , where
, where 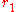 denotes the number of real embeddings of K, and
denotes the number of real embeddings of K, and 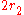 is the number of complex embeddings of
is the number of complex embeddings of  Let
Let
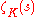
be the Dedekind zeta function of Also define the following invariants
Also define the following invariants
:
Then:
Theorem 1 (Class Number Formula) The Dedekind zeta function
of K,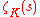 converges absolutely for
converges absolutely for 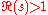 and extends to a meromorphic function
and extends to a meromorphic function
defined for all complex s with only one simple pole at with residue
with residue
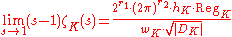
This is the most general "class number formula". In particular cases, for example when K is a cyclotomic extension of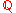 , there are particular and more refined class number formulas.
, there are particular and more refined class number formulas.
of Q, the theory of Artin L-function
s applies to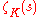 . It has one factor of the Riemann zeta function, which has a pole of residue one, and the quotient is regular at s = 1. This means that the right-hand side of the class number formula can be equated to a left-hand side
. It has one factor of the Riemann zeta function, which has a pole of residue one, and the quotient is regular at s = 1. This means that the right-hand side of the class number formula can be equated to a left-hand side
with ρ running over the classes of irreducible complex linear representations of Gal(K/Q) of dimension dim(ρ). That is according to the standard decomposition of the regular representation
.
, in which all the ρ can be replaced by Dirichlet character
s (via class field theory
) for some modulus f called the conductor. Therefore all the L(1) values occur for Dirichlet L-functions, for which there is a classical formula, involving logarithms.
By the Kronecker–Weber theorem
, all the values required for an analytic class number formula occur already when the cyclotomic fields are considered. In that case there is a further formulation possible, as shown by Kummer
. The regulator, a calculation of volume in 'logarithmic space' as divided by the logarithms of the units of the cyclotomic field, can be set against the quantities from the L(1) recognisable as logarithms of cyclotomic unit
s. There result formulae stating that the class number is determined by the index of the cyclotomic units in the whole group of units.
In Iwasawa theory
, these ideas are further combined with Stickelberger's theorem
.
The first class number formula was proved by Dirichlet in 1839, but it was proved about classes of quadratic forms rather than classes of ideal
s. Let d be a fundamental discriminant
, and write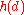 for the number of equivalence classes of quadratic forms with discriminant d. Let
for the number of equivalence classes of quadratic forms with discriminant d. Let 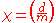 be the Kronecker symbol
be the Kronecker symbol
. Then is a Dirichlet character
is a Dirichlet character
. Write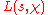 for the Dirichlet L-series based on
for the Dirichlet L-series based on  . For
. For  , let
, let  ,
,  be the solution to the Pell equation
be the solution to the Pell equation 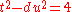 for which u is smallest, and write
for which u is smallest, and write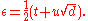
(Then is either a fundamental unit
is either a fundamental unit
of the real quadratic field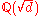 or the square of a fundamental unit.)
or the square of a fundamental unit.)
For , write w for the number of automorphs of quadratic forms of discriminant d; that is,
, write w for the number of automorphs of quadratic forms of discriminant d; that is,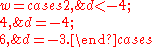
Then Dirichlet showed that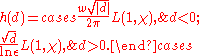
This is a special case of Theorem 1 above: for a quadratic field
K, the Dedekind zeta function is just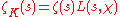 , and the residue is
, and the residue is 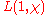 .
.
Dirichlet also showed that the L-series can be written in a finite form, which gives a finite form for the class number. We have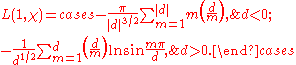
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the class number formula relates many important invariants of a number field to a special value of its Dedekind zeta function
Dedekind zeta function
In mathematics, the Dedekind zeta function of an algebraic number field K, generally denoted ζK, is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational numbers Q...
General statement of the class number formula
Let K be a number field with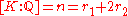 , where
, where 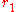 denotes the number of real embeddings of K, and
denotes the number of real embeddings of K, and 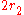 is the number of complex embeddings of
is the number of complex embeddings of  Let
Let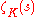
be the Dedekind zeta function of
 Also define the following invariants
Also define the following invariantsInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
:
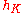 is the class number, the number of elements in the ideal class group of
is the class number, the number of elements in the ideal class group of 
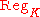 is the regulator of
is the regulator of 
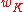 is the number of roots of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
is the number of roots of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
contained in
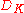 is the discriminantDiscriminant of an algebraic number fieldIn mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
is the discriminantDiscriminant of an algebraic number fieldIn mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of the extensionAlgebraic extensionIn abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
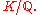
Then:
Theorem 1 (Class Number Formula) The Dedekind zeta function
Dedekind zeta function
In mathematics, the Dedekind zeta function of an algebraic number field K, generally denoted ζK, is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational numbers Q...
of K,
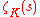 converges absolutely for
converges absolutely for 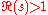 and extends to a meromorphic function
and extends to a meromorphic functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
defined for all complex s with only one simple pole at
 with residue
with residue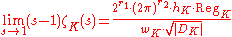
This is the most general "class number formula". In particular cases, for example when K is a cyclotomic extension of
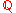 , there are particular and more refined class number formulas.
, there are particular and more refined class number formulas.Galois extensions of the rationals
If K is a Galois extensionGalois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of Q, the theory of Artin L-function
Artin L-function
In mathematics, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group G. These functions were introduced in the 1923 by Emil Artin, in connection with his research into class field theory. Their fundamental properties, in particular the Artin...
s applies to
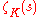 . It has one factor of the Riemann zeta function, which has a pole of residue one, and the quotient is regular at s = 1. This means that the right-hand side of the class number formula can be equated to a left-hand side
. It has one factor of the Riemann zeta function, which has a pole of residue one, and the quotient is regular at s = 1. This means that the right-hand side of the class number formula can be equated to a left-hand side- Π L(1,ρ)dim ρ
with ρ running over the classes of irreducible complex linear representations of Gal(K/Q) of dimension dim(ρ). That is according to the standard decomposition of the regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
.
Abelian extensions of the rationals
This is the case of the above, with Gal(K/Q) an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, in which all the ρ can be replaced by Dirichlet character
Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
s (via class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
) for some modulus f called the conductor. Therefore all the L(1) values occur for Dirichlet L-functions, for which there is a classical formula, involving logarithms.
By the Kronecker–Weber theorem
Kronecker–Weber theorem
In algebraic number theory, the Kronecker–Weber theorem states that every finite abelian extension of the field of rational numbers Q, or in other words, every algebraic number field whose Galois group over Q is abelian, is a subfield of a cyclotomic field, i.e. a field obtained by adjoining a root...
, all the values required for an analytic class number formula occur already when the cyclotomic fields are considered. In that case there is a further formulation possible, as shown by Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
. The regulator, a calculation of volume in 'logarithmic space' as divided by the logarithms of the units of the cyclotomic field, can be set against the quantities from the L(1) recognisable as logarithms of cyclotomic unit
Cyclotomic unit
In mathematics, a cyclotomic unit is a unit of an algebraic number field of the form / for ζ a root of unity, or more generally a unit that can be written as a product of these and a root of unity....
s. There result formulae stating that the class number is determined by the index of the cyclotomic units in the whole group of units.
In Iwasawa theory
Iwasawa theory
In number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa, in the 1950s, as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur...
, these ideas are further combined with Stickelberger's theorem
Stickelberger's theorem
In mathematics, Stickelberger's theorem is a result of algebraic number theory, which gives some information about the Galois module structure of class groups of cyclotomic fields...
.
Dirichlet class number formula
This exposition follows Davenport.The first class number formula was proved by Dirichlet in 1839, but it was proved about classes of quadratic forms rather than classes of ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
s. Let d be a fundamental discriminant
Fundamental discriminant
In mathematics, a fundamental discriminant D is an integer invariant in the theory of integral binary quadratic forms. If is a quadratic form with integer coefficients, then is the discriminant of Q. Conversely, every integer D with is the discriminant of some binary quadratic form with integer...
, and write
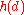 for the number of equivalence classes of quadratic forms with discriminant d. Let
for the number of equivalence classes of quadratic forms with discriminant d. Let 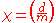 be the Kronecker symbol
be the Kronecker symbolKronecker symbol
In number theory, the Kronecker symbol, written as \left or , is a generalization of the Jacobi symbol to all integers n. It was introduced by Leopold Kronecker.-Definition:...
. Then
 is a Dirichlet character
is a Dirichlet characterDirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
. Write
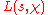 for the Dirichlet L-series based on
for the Dirichlet L-series based on  . For
. For  , let
, let  ,
,  be the solution to the Pell equation
be the solution to the Pell equation 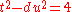 for which u is smallest, and write
for which u is smallest, and write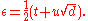
(Then
 is either a fundamental unit
is either a fundamental unitFundamental unit (number theory)
In algebraic number theory, a fundamental unit is a generator for the torsion-free unit group of the ring of integers of a number field, when that group is infinite cyclic...
of the real quadratic field
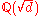 or the square of a fundamental unit.)
or the square of a fundamental unit.)For
 , write w for the number of automorphs of quadratic forms of discriminant d; that is,
, write w for the number of automorphs of quadratic forms of discriminant d; that is,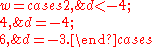
Then Dirichlet showed that
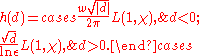
This is a special case of Theorem 1 above: for a quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
K, the Dedekind zeta function is just
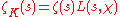 , and the residue is
, and the residue is 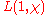 .
.Dirichlet also showed that the L-series can be written in a finite form, which gives a finite form for the class number. We have