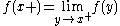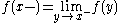Dirichlet conditions
Encyclopedia
In mathematics
, the Dirichlet conditions are sufficient conditions for a real-valued, periodic function
f(x) to be equal to the sum of its Fourier series
at each point where f is continuous
. Moreover, the behavior of the Fourier series at points of discontinuity is determined as well. These conditions are named after Johann Peter Gustav Lejeune Dirichlet
.
The conditions are:

The analogous statement holds irrespective of what the period of f is, or which version of the Fourier expansion is chosen (see Fourier series
).
A function satisfying Dirichlet's conditions must have right and left limits at each point of discontinuity, or else the function would need to oscillate at that point, violating the condition on maxima/minima. Note that at any point where f is continuous,
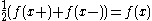 .
.
Thus Dirichlet's theorem says in particular that the Fourier series for f converges and is equal to f wherever f is continuous.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Dirichlet conditions are sufficient conditions for a real-valued, periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
f(x) to be equal to the sum of its Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
at each point where f is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Moreover, the behavior of the Fourier series at points of discontinuity is determined as well. These conditions are named after Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
.
The conditions are:
- f(x) must have a finite number of extremaMaxima and minimaIn mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
in any given interval - f(x) must have a finite number of discontinuitiesClassification of discontinuitiesContinuous functions are of utmost importance in mathematics and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there...
in any given interval - f(x) must be absolutely integrable over a period.
- f(x) must be boundedBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
Dirichlet's Theorem for 1-Dimensional Fourier Series
We state Dirichlet's theorem assuming f is a periodic function of period 2π with Fourier series expansion where
The analogous statement holds irrespective of what the period of f is, or which version of the Fourier expansion is chosen (see Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
).
- Dirichlet's theorem: If f satisfies Dirichlet conditions, then for all x, we have that the series obtained by plugging x into the Fourier series is convergent, and is given by
-
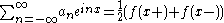 ,
,
- where the notation
- denotes the right/left limits of f.
A function satisfying Dirichlet's conditions must have right and left limits at each point of discontinuity, or else the function would need to oscillate at that point, violating the condition on maxima/minima. Note that at any point where f is continuous,
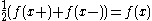 .
.Thus Dirichlet's theorem says in particular that the Fourier series for f converges and is equal to f wherever f is continuous.