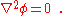Siméon Denis Poisson
Encyclopedia
Siméon Denis Poisson was a French
mathematician
, geometer, and physicist
. He however, was the final leading opponent of the wave theory of light as a member of the elite l'Académie française
, but was proven wrong by Augustin-Jean Fresnel
.
, Loiret
, the son of soldier Siméon Poisson.
In 1798, he entered the École Polytechnique
in Paris
as first in his year, and immediately began to attract the notice of the professors of the school, who left him free to make his own choices as to what he would study. In 1800, less than two years after his entry, he published two memoirs, one on Étienne Bézout
's method of elimination, the other on the number of integral
s of a finite difference
equation. The latter was examined by Sylvestre-François Lacroix and Adrien-Marie Legendre
, who recommended that it should be published in the Recueil des savants étrangers, an unprecedented honour for a youth of eighteen. This success at once procured entry for Poisson into scientific circles. Joseph Louis Lagrange
, whose lectures on the theory of functions he attended at the École Polytechnique, recognized his talent early on, and became his friend (the Mathematics Genealogy Project
lists Lagrange as his advisor, but this may be an approximation); while Pierre-Simon Laplace
, in whose footsteps Poisson followed, regarded him almost as his son. The rest of his career, till his death in Sceaux
near Paris, was almost entirely occupied by the composition and publication of his many works and in fulfilling the duties of the numerous educational positions to which he was successively appointed.
Immediately after finishing his studies at the École Polytechnique, he was appointed répétiteur
(teaching assistant) there, a position which he had occupied as an amateur while still a pupil in the school; for his schoolmates had made a custom of visiting him in his room after an unusually difficult lecture to hear him repeat and explain it. He was made deputy professor (professeur suppléant) in 1802, and, in 1806 full professor succeeding Jean Baptiste Joseph Fourier, whom Napoleon had sent to Grenoble
. In 1808 he became astronomer
to the Bureau des Longitudes
; and when the Faculté des Sciences was instituted in 1809 he was appointed professor of rational mechanics (professeur de mécanique rationelle). He went on to become a member of the Institute in 1812, examiner at the military school (École Militaire) at Saint-Cyr
in 1815, graduation examiner at the École Polytechnique in 1816, councillor of the university in 1820, and geometer to the Bureau des Longitudes succeeding Pierre-Simon Laplace in 1827.
In 1817, he married Nancy de Bardi and with her he had four children. His father, whose early experiences had led him to hate aristocrats, bred him in the stern creed of the First Republic. Throughout the Revolution, the Empire, and the following restoration, Poisson was not interested in politics, concentrating on mathematics. He was appointed to the dignity of baron
in 1821; but he neither took out the diploma or used the title. In March 1818, he was elected a Fellow of the Royal Society and in 1823 a foreign member of the Royal Swedish Academy of Sciences
. The revolution of July 1830
threatened him with the loss of all his honours; but this disgrace to the government of Louis-Philippe
was adroitly averted by François Jean Dominique Arago, who, while his "revocation" was being plotted by the council of ministers, procured him an invitation to dine at the Palais Royal, where he was openly and effusively received by the citizen king, who "remembered" him. After this, of course, his degradation was impossible, and seven years later he was made a peer of France, not for political reasons, but as a representative of French science
.
As a teacher of mathematics Poisson is said to have been extraordinarily successful, as might have been expected from his early promise as a répétiteur at the École Polytechnique. As a scientific worker, his productivity has rarely if ever been equalled. Notwithstanding his many official duties, he found time to publish more than three hundred works, several of them extensive treatises, and many of them memoirs dealing with the most abstruse branches of pure mathematics, applied mathematics
, mathematical physics
, and rational mechanics. (Arago
attributed to him the quote, "Life is good for only two things: doing mathematics and teaching it.")
A list of Poisson's works, drawn up by himself, is given at the end of Arago's biography. All that is possible is a brief mention of the more important ones. It was in the application of mathematics to physics that his greatest services to science were performed. Perhaps the most original, and certainly the most permanent in their influence, were his memoirs on the theory of electricity
and magnetism
, which virtually created a new branch of mathematical physics.
Next (or in the opinion of some, first) in importance stand the memoirs on celestial mechanics, in which he proved himself a worthy successor to Pierre-Simon Laplace. The most important of these are his memoirs Sur les inégalités séculaires des moyens mouvements des planètes, Sur la variation des constantes arbitraires dans les questions de mécanique, both published in the Journal of the École Polytechnique (1809); Sur la libration de la lune, in Connaissances des temps (1821), etc.; and Sur le mouvement de la terre autour de son centre de gravité, in Mémoires de l'Académie (1827), etc. In the first of these memoirs, Poisson discusses the famous question of the stability of the planetary orbit
s, which had already been settled by Lagrange to the first degree of approximation for the disturbing forces. Poisson showed that the result could be extended to a second approximation, and thus made an important advance in planetary theory. The memoir is remarkable inasmuch as it roused Lagrange, after an interval of inactivity, to compose in his old age one of the greatest of his memoirs, entitled Sur la théorie des variations des éléments des planètes, et en particulier des variations des grands axes de leurs orbites. So highly did he think of Poisson's memoir that he made a copy of it with his own hand, which was found among his papers after his death. Poisson made important contributions to the theory of attraction.
His name is one of the 72 names inscribed on the Eiffel Tower.
for potential
:
today named after him Poisson's equation
or the potential theory
equation, was first published in the Bulletin de la société philomatique (1813). If a function of a given point ρ = 0, we get Laplace's equation
:
In 1812 Poisson discovered that Laplace's equation is valid only outside of a solid. A rigorous proof for masses with variable density was first given by Carl Friedrich Gauss
in 1839. Both equations have their equivalents in vector algebra. Poisson's equation for the divergence of the gradient
of a scalar field
, φ in 3-dimensional space is:
Consider for instance Poisson's equation for surface electrical potential, Ψ as a function of the density of electric charge, ρe at a particular point:
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, geometer, and physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
. He however, was the final leading opponent of the wave theory of light as a member of the elite l'Académie française
Académie française
L'Académie française , also called the French Academy, is the pre-eminent French learned body on matters pertaining to the French language. The Académie was officially established in 1635 by Cardinal Richelieu, the chief minister to King Louis XIII. Suppressed in 1793 during the French Revolution,...
, but was proven wrong by Augustin-Jean Fresnel
Augustin-Jean Fresnel
Augustin-Jean Fresnel , was a French engineer who contributed significantly to the establishment of the theory of wave optics. Fresnel studied the behaviour of light both theoretically and experimentally....
.
Biography
Poisson was born in PithiviersPithiviers
Pithiviers is a commune in the Loiret department in north-central France. It is twinned with Ashby-de-la-Zouch in Leicestershire, England....
, Loiret
Loiret
Loiret is a department in north-central FranceThe department is named after the river Loiret, a tributary of the Loire. The Loiret is located wholly within the department.- History :...
, the son of soldier Siméon Poisson.
In 1798, he entered the École Polytechnique
École Polytechnique
The École Polytechnique is a state-run institution of higher education and research in Palaiseau, Essonne, France, near Paris. Polytechnique is renowned for its four year undergraduate/graduate Master's program...
in Paris
Paris
Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...
as first in his year, and immediately began to attract the notice of the professors of the school, who left him free to make his own choices as to what he would study. In 1800, less than two years after his entry, he published two memoirs, one on Étienne Bézout
Étienne Bézout
-External links:...
's method of elimination, the other on the number of integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s of a finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
equation. The latter was examined by Sylvestre-François Lacroix and Adrien-Marie Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
, who recommended that it should be published in the Recueil des savants étrangers, an unprecedented honour for a youth of eighteen. This success at once procured entry for Poisson into scientific circles. Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
, whose lectures on the theory of functions he attended at the École Polytechnique, recognized his talent early on, and became his friend (the Mathematics Genealogy Project
Mathematics Genealogy Project
The Mathematics Genealogy Project is a web-based database for the academic genealogy of mathematicians. As of September, 2010, it contained information on approximately 145,000 mathematical scientists who contribute to "research-level mathematics"...
lists Lagrange as his advisor, but this may be an approximation); while Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
, in whose footsteps Poisson followed, regarded him almost as his son. The rest of his career, till his death in Sceaux
Sceaux, Hauts-de-Seine
Sceaux is a commune in the southern suburbs of Paris, France. It is located from the center of Paris.-Wealth:Sceaux is famous for the Château of Sceaux, set in its large park , designed by André Le Nôtre, measuring...
near Paris, was almost entirely occupied by the composition and publication of his many works and in fulfilling the duties of the numerous educational positions to which he was successively appointed.
Immediately after finishing his studies at the École Polytechnique, he was appointed répétiteur
Répétiteur
Répétiteur , repetitore , or Korrepetitor / Repetitor , originally from the French verb répéter meaning "to repeat, to go over, to learn, to rehearse"....
(teaching assistant) there, a position which he had occupied as an amateur while still a pupil in the school; for his schoolmates had made a custom of visiting him in his room after an unusually difficult lecture to hear him repeat and explain it. He was made deputy professor (professeur suppléant) in 1802, and, in 1806 full professor succeeding Jean Baptiste Joseph Fourier, whom Napoleon had sent to Grenoble
Grenoble
Grenoble is a city in southeastern France, at the foot of the French Alps where the river Drac joins the Isère. Located in the Rhône-Alpes region, Grenoble is the capital of the department of Isère...
. In 1808 he became astronomer
Astronomer
An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
to the Bureau des Longitudes
Bureau des Longitudes
The Bureau des Longitudes is a French scientific institution, founded by decree of 25 June 1795 and charged with the improvement of nautical navigation, standardisation of time-keeping, geodesy and astronomical observation. During the 19th century, it was responsible for synchronizing clocks...
; and when the Faculté des Sciences was instituted in 1809 he was appointed professor of rational mechanics (professeur de mécanique rationelle). He went on to become a member of the Institute in 1812, examiner at the military school (École Militaire) at Saint-Cyr
École Spéciale Militaire de Saint-Cyr
The École Spéciale Militaire de Saint-Cyr is the foremost French military academy. Its official name is . It is often referred to as Saint-Cyr . Its motto is "Ils s'instruisent pour vaincre": literally "They study to vanquish" or "Training for victory"...
in 1815, graduation examiner at the École Polytechnique in 1816, councillor of the university in 1820, and geometer to the Bureau des Longitudes succeeding Pierre-Simon Laplace in 1827.
In 1817, he married Nancy de Bardi and with her he had four children. His father, whose early experiences had led him to hate aristocrats, bred him in the stern creed of the First Republic. Throughout the Revolution, the Empire, and the following restoration, Poisson was not interested in politics, concentrating on mathematics. He was appointed to the dignity of baron
Baron
Baron is a title of nobility. The word baron comes from Old French baron, itself from Old High German and Latin baro meaning " man, warrior"; it merged with cognate Old English beorn meaning "nobleman"...
in 1821; but he neither took out the diploma or used the title. In March 1818, he was elected a Fellow of the Royal Society and in 1823 a foreign member of the Royal Swedish Academy of Sciences
Royal Swedish Academy of Sciences
The Royal Swedish Academy of Sciences or Kungliga Vetenskapsakademien is one of the Royal Academies of Sweden. The Academy is an independent, non-governmental scientific organization which acts to promote the sciences, primarily the natural sciences and mathematics.The Academy was founded on 2...
. The revolution of July 1830
July Revolution
The French Revolution of 1830, also known as the July Revolution or in French, saw the overthrow of King Charles X of France, the French Bourbon monarch, and the ascent of his cousin Louis-Philippe, Duke of Orléans, who himself, after 18 precarious years on the throne, would in turn be overthrown...
threatened him with the loss of all his honours; but this disgrace to the government of Louis-Philippe
Louis-Philippe of France
Louis Philippe I was King of the French from 1830 to 1848 in what was known as the July Monarchy. His father was a duke who supported the French Revolution but was nevertheless guillotined. Louis Philippe fled France as a young man and spent 21 years in exile, including considerable time in the...
was adroitly averted by François Jean Dominique Arago, who, while his "revocation" was being plotted by the council of ministers, procured him an invitation to dine at the Palais Royal, where he was openly and effusively received by the citizen king, who "remembered" him. After this, of course, his degradation was impossible, and seven years later he was made a peer of France, not for political reasons, but as a representative of French science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
.
As a teacher of mathematics Poisson is said to have been extraordinarily successful, as might have been expected from his early promise as a répétiteur at the École Polytechnique. As a scientific worker, his productivity has rarely if ever been equalled. Notwithstanding his many official duties, he found time to publish more than three hundred works, several of them extensive treatises, and many of them memoirs dealing with the most abstruse branches of pure mathematics, applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, and rational mechanics. (Arago
François Arago
François Jean Dominique Arago , known simply as François Arago , was a French mathematician, physicist, astronomer and politician.-Early life and work:...
attributed to him the quote, "Life is good for only two things: doing mathematics and teaching it.")
A list of Poisson's works, drawn up by himself, is given at the end of Arago's biography. All that is possible is a brief mention of the more important ones. It was in the application of mathematics to physics that his greatest services to science were performed. Perhaps the most original, and certainly the most permanent in their influence, were his memoirs on the theory of electricity
Electricity
Electricity is a general term encompassing a variety of phenomena resulting from the presence and flow of electric charge. These include many easily recognizable phenomena, such as lightning, static electricity, and the flow of electrical current in an electrical wire...
and magnetism
Magnetism
Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well...
, which virtually created a new branch of mathematical physics.
Next (or in the opinion of some, first) in importance stand the memoirs on celestial mechanics, in which he proved himself a worthy successor to Pierre-Simon Laplace. The most important of these are his memoirs Sur les inégalités séculaires des moyens mouvements des planètes, Sur la variation des constantes arbitraires dans les questions de mécanique, both published in the Journal of the École Polytechnique (1809); Sur la libration de la lune, in Connaissances des temps (1821), etc.; and Sur le mouvement de la terre autour de son centre de gravité, in Mémoires de l'Académie (1827), etc. In the first of these memoirs, Poisson discusses the famous question of the stability of the planetary orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s, which had already been settled by Lagrange to the first degree of approximation for the disturbing forces. Poisson showed that the result could be extended to a second approximation, and thus made an important advance in planetary theory. The memoir is remarkable inasmuch as it roused Lagrange, after an interval of inactivity, to compose in his old age one of the greatest of his memoirs, entitled Sur la théorie des variations des éléments des planètes, et en particulier des variations des grands axes de leurs orbites. So highly did he think of Poisson's memoir that he made a copy of it with his own hand, which was found among his papers after his death. Poisson made important contributions to the theory of attraction.
His name is one of the 72 names inscribed on the Eiffel Tower.
Contributions
Poisson's well-known correction of Laplace's second order partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
for potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
:
today named after him Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
or the potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
equation, was first published in the Bulletin de la société philomatique (1813). If a function of a given point ρ = 0, we get Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
:
In 1812 Poisson discovered that Laplace's equation is valid only outside of a solid. A rigorous proof for masses with variable density was first given by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in 1839. Both equations have their equivalents in vector algebra. Poisson's equation for the divergence of the gradient
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
of a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
, φ in 3-dimensional space is:
Consider for instance Poisson's equation for surface electrical potential, Ψ as a function of the density of electric charge, ρe at a particular point:
-
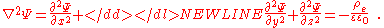
The distribution of a charge in a fluidFluidIn physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
is unknown and we have to use the Poisson-Boltzmann equationPoisson-Boltzmann equationThe Poisson–Boltzmann equation is a differential equation that describes electrostatic interactions between molecules in ionic solutions. It is the mathematical base for the Gouy–Chapman double layer theory; first proposed by Gouy in 1910 and complemented by Chapman in 1913...
:

which in most cases cannot be solved analytically. In polar coordinates the Poisson-Boltzmann equation is:

which also cannot be solved analytically. If a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, φ is not scalarScalar fieldIn mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
, the Poisson equation is valid, as can be for example in 4-dimensional Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
:
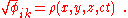
If ρ(x, y, z) is a continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and if for r→ ∞ (or if a point 'moves' to infinityExtended real number lineIn mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
) a function φ goes to 0 fast enough, a solution of Poisson's equation is the Newtonian potentialNewtonian potentialIn mathematics, the Newtonian potential or Newton potential is an operator in vector calculus that acts as the inverse to the negative Laplacian, on functions that are smooth and decay rapidly enough at infinity. As such, it is a fundamental object of study in potential theory...
of a function ρ(x, y, z):
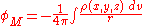
where r is a distance between a volume element dv and a point M. The integration runs over the whole space.
Another "Poisson's integral" is the solution for the Green functionGreen functionGreen function might refer to:*Green's function of a differential operator.*Deligne–Lusztig theory in the representation theory of finite groups of Lie type.*Green's function in many-body theory....
for Laplace's equation with Dirichlet condition over a circular disk:
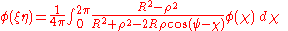
where


- φ is a boundary condition holding on the disk's boundary.
In the same manner, we define the Green function for the Laplace equation with Dirichlet condition, ∇² φ = 0 over a sphere of radius R. This time the Green function is:
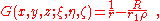
where
 is the distance of a point (ξ, η, ζ) from the center of a sphere,
is the distance of a point (ξ, η, ζ) from the center of a sphere,
r is the distance between points (x, y, z) and (ξ, η, ζ), and
r1 is the distance between the point (x, y, z) and the point (Rξ/ρ, Rη/ρ, Rζ/ρ), symmetrical to the point (ξ, η, ζ).
Poisson's integral now has a form:
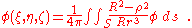
Poisson's two most important memoirs on the subject are Sur l'attraction des sphéroides (Connaiss. ft. temps, 1829), and Sur l'attraction d'un ellipsoide homogène (Mim. ft. l'acad., 1835). In concluding our selection from his physical memoirs, we may mention his memoir on the theory of waves (Mém. ft. l'acad., 1825).
In pure mathematicsPure mathematicsBroadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
, his most important works were his series of memoirs on definite integrals and his discussion of Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, the latter paving the way for the classic researches of Peter Gustav Lejeune Dirichlet and Bernhard RiemannBernhard RiemannGeorg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
on the same subject; these are to be found in the Journal of the École Polytechnique from 1813 to 1823, and in the Memoirs de l'Académie for 1823. He also studied Fourier integrals. We may also mention his essay on the calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
(Mem. de l'acad., 1833), and his memoirs on the probability of the mean results of observations (Connaiss. d. temps, 1827, &c). The Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
in probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
is named after him.
In his Traité de mécanique (2 vols. 8vo, 1811 arid 1833), which was written in the style of Laplace and Lagrange and was long a standard work, he showed many novelties such as an explicit usage of momentaMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
:
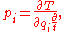
which influenced the work of HamiltonWilliam Rowan HamiltonSir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
and JacobiCarl Gustav Jakob JacobiCarl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
.
Besides his many memoirs, Poisson published a number of treatises, most of which were intended to form part of a great work on mathematical physics, which he did not live to complete. Among these may be mentioned- Nouvelle théorie de l'action capillaire (4to, 1831);
- Théorie mathématique de la chaleur (4to, 1835);
- Supplement to the same (4to, 1837);
- Recherches sur la probabilité des jugements en matières criminelles et matière civile (4to, 1837), all published at Paris.
A translation of Poisson's Treatise on Mechanics was published in London in 1842.
In 1815 Poisson studied integrations along paths in the complex plane. In 1831 he derived the Navier-Stokes equationsNavier-Stokes equationsIn physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
independently of Claude-Louis NavierClaude-Louis NavierClaude-Louis Navier born Claude Louis Marie Henri Navier , was a French engineer and physicist who specialized in mechanics.The Navier–Stokes equations are named after him and George Gabriel Stokes....
.
Flawed views on the wave theory of light
Poisson, despite his brilliance, had surprising hubris on the wave theory of light. He was a member of the academic "old guard" at the Académie françaiseAcadémie françaiseL'Académie française , also called the French Academy, is the pre-eminent French learned body on matters pertaining to the French language. The Académie was officially established in 1635 by Cardinal Richelieu, the chief minister to King Louis XIII. Suppressed in 1793 during the French Revolution,...
, who were staunch believers in the particle theory of light who were alarmed at the wave theory of light's increasing acceptance. In 1818, the Académie française set their prize as diffractionDiffractionDiffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
, being certain that a particle theorist would win it. Poisson, relying on intuition rather than mathematics or scientific experiment, ridiculed participant and civil engineer Augustin-Jean FresnelAugustin-Jean FresnelAugustin-Jean Fresnel , was a French engineer who contributed significantly to the establishment of the theory of wave optics. Fresnel studied the behaviour of light both theoretically and experimentally....
when he submitted a thesis explaining diffraction derived from analysis of both the Huygens–Fresnel principle and Young's double slit experiment.
Poisson studied Fresnel's theory in detail and of course looked for a way to prove it wrong, as he was a dogmatic supporter of the particle-theory of light. Poisson thought that he had found a flaw when he argued that a consequence of Fresnel’s theory was that there would exist an on-axis bright spot in the shadow of a circular obstacle blocking a point sourcePoint sourceA point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
of light, where there should be complete darkness according to the particle-theory of light. Fresnel's theory could not be true, Poisson declared, surely this result was absurd. (The Poisson spot is not easily observed in every-day situations, because most everyday sources of light are not good point sources.)
However, the head of the committee, Dominique-François-Jean AragoFrançois AragoFrançois Jean Dominique Arago , known simply as François Arago , was a French mathematician, physicist, astronomer and politician.-Early life and work:...
, and who incidentally later became Prime Minister of France, did not have the hubris of Poisson and decided it was necessary to perform the experiment in more detail. He molded a 2-mm metallic disk to a glass plate with wax.
To everyone's surprise he succeeded in observing the predicted spot, which convinced most scientists of the wave-nature of light. In the end Fresnel won the competition, much to Poisson's chagrin.
After that, the corpuscular theory of light was vanquished, not to be heard of again till the 20th century developed wave-particle duality. Arago later noted that the diffraction phenomenon (which was later to be known as the Arago spotArago spotIn optics, an Arago spot, Fresnel bright spot, or Poisson spot is a bright point that appears at the center of a circular object's shadow due to Fresnel diffraction...
) had already been observed by Joseph-Nicolas DelisleJoseph-Nicolas DelisleJoseph-Nicolas Delisle was a French astronomer.-Life:He was one of the 11 sons of Claude Delisle . Like many of his brothers, among them Guillaume Delisle, he initially followed classical studies. Soon however, he moved to astronomy under the supervision of Joseph Lieutaud and Jacques Cassini...
and Giacomo F. MaraldiGiacomo F. MaraldiGiacomo Filippo Maraldi was an French-Italian astronomer and mathematician. His name is also given as Jacques Philippe Maraldi....
a century earlier.