Glossary of scheme theory
Encyclopedia
This is a glossary of scheme theory. For an introduction to the theory of schemes in algebraic geometry
, see affine scheme, projective space
, sheaf
and scheme
. The concern here is to list the fundamental technical definitions and properties of scheme theory. See also list of algebraic geometry topics.
is a locally ringed space, so a fortiori a topological space
, but the meanings of point of
are threefold:
Geometric points are what in the most classical cases, for example algebraic varieties that are complex manifold
s, would be the ordinary-sense points. The points
of the underlying space include analogues of the generic point
s (in the sense of Zariski, not that of André Weil
), which specialise to ordinary-sense points. The
-valued points are thought of, via Yoneda's lemma, as a way of identifying 
with the representable functor
it sets up. Historically there was a process by which projective geometry
added more points (e.g. complex points, line at infinity
) to simplify the geometry by refining the basic objects. The
-valued points were a massive further step.
As part of the predominating Grothendieck approach
, there are three corresponding notions of fiber of a morphism: the first being the simple inverse image of a point. The other two are formed by creating fiber products of two morphisms. For example, a geometric fiber of a morphism
is thought of as
.
This makes the extension from affine schemes, where it is just the tensor product of R-algebras, to all schemes of the fiber product operation a significant (if technically anodyne) result.
Xi, every Xi has the property P. It is usually the case that is enough to check one cover, not all possible ones. One also says that a certain property is Zariski-local, if one needs to distinguish between the Zariski topology
and other possible topologies, like the étale topology
.
Consider a scheme X and a cover by affine open subschemes Spec Ai. Using the dictionary between (commutative) rings
and affine schemes local properties are thus properties of the rings Ai. A property P is local in the above sense, iff the corresponding property of rings is stable under localization
.
For example, we can speak of locally Noetherian schemes, namely those which are covered by the spectra of Noetherian ring
s. The fact that localizations of a Noetherian ring are still noetherian then means that the property of a scheme of being locally Noetherian is local in the above sense (whence the name). Another example: if a ring is reduced
(i.e., has no non-zero nilpotent
elements), then so are its localizations.
An example for a non-local property is separatedness (see below for the definition). Any affine scheme is separated, therefore any scheme is locally separated. However, the affine pieces may glue together pathologically to yield a non-separated scheme.
The following is a (non-exhaustive) list of local properties of rings, which are applied to schemes. Let X =
Spec Ai be a covering of a scheme by open affine subschemes. For definiteness, let k denote a field
in the following. Most of the examples also work with the integers Z as a base, though, or even more general bases.
of integers; so that any scheme 
is over 
, and in a unique way.
For the following definitions, we take as standard notation
to be a morphism of schemes. Parallel to the properties of schemes above, the following properties of morphisms are also of local nature, i.e. if there is an open covering of
by some open subschemes 
, such that the restriction of 
to 
has the property, then 
has it, as well.
A morphism is called dominant, if the image f(Y) is dense
. A morphism of affine schemes Spec A → Spec B is dense if and only if the kernel of the corresponding map B → A is contained in the nilradical of A.
A morphism is called quasi-compact, if for some (equivalently: every) open affine cover of X by some Ui = Spec Bi, the preimages f−1(Ui) are quasi-compact.
.
Closed subschemes of a scheme X are defined to be those occurring in the following construction. Let J be a quasi-coherent sheaf of
-ideals. The support of the quotient sheaf 
is a closed subset Z of X and 
is a scheme called the closed subscheme defined by the quasi-coherent sheaf of ideals J. The reason the definition of closed subschemes relies on such a construction is that, unlike open subsets, a closed subset of a scheme does not have a unique structure as a subscheme.
A subscheme, without qualifier, of X is a closed subscheme of an open subscheme of X.
Immersions are maps that factor through isomorphisms with subschemes. Specifically, an open immersion factors through an isomorphism with an open subscheme and a closed immersion factors through an isomorphism with a closed subscheme. Equivalently, f is a closed immersion if, and only if, it induces a homeomorphism from the underlying topological space of Y to a closed subset of the underlying topological space of X, and if the morphism
is surjective. A composition of immersions is again an immersion.
Some authors, such as Hartshorne in his book Algebraic Geometry and Q. Liu in his book Algebraic Geometry and Arithmetic Curves, define immersions as the composite of an open immersion followed by a closed immersion. These immersions are immersions in the sense above, but the converse is false. Furthermore, under this definition, the composite of two immersions is not necessarily an immersion. However, the two definitions are equivalent when f is quasi-compact.
Note that an open immersion is completely described by its image in the sense of topological spaces, while a closed immersion is not:
and 
may be homeomorphic but not isomorphic. This happens, for example, if I is the radical of J but J is not a radical ideal. When specifying a closed subset of a scheme without mentioning the scheme structure, usually the so-called reduced scheme structure is meant, that is, the scheme structure corresponding to the unique radical ideal consisting of all functions vanishing on that closed subset.
. Important affine morphisms are vector bundle
s, and finite morphisms.
Projective morphisms are defined similarly, but in practice they turn out to be more important than affine morphisms:
is called projective if it factors as a closed immersion followed by the projection of a projective space
to 
. Again, one may say, that 
is projective if it is given by the global Proj construction on graded commutative OX-Algebras.
such that the fiber product of 
with itself along 
has its diagonal
as a closed subscheme — in other words, the diagonal map is a closed immersion.
As a consequence, a scheme
is separated when the diagonal of 
within the scheme product of 
with itself is a closed immersion. Emphasizing the relative point of view, one might equivalently define a scheme to be separated if the unique morphism 
is separated.
Notice that for a topological space
Y is Hausdorff iff the diagonal embedding
is closed. In algebraic geometry, the above formulation is used because a scheme is a Hausdorff space if and only if it is zero-dimensional. The difference between the topological and algebro-geometric context comes from the topological structure of the fiber product (in the category of schemes)
, which is different from the product of topological spaces.
Any affine scheme Spec A is separated, because the diagonal corresponds to the surjective map of rings (hence is a closed immersion of schemes):
.
A morphism is called quasi-separated or (X is quasi-separated over Y) if the diagonal morphism is quasi-compact. A scheme X is called quasi-separated if X is quasi-separated over Spec(Z).
While the separatedness is of rather technical nature, properness has deep geometrical meaning.
A morphism is proper if it is separated, universally closed (i.e. such that fiber products with it preserve closed immersions), and of finite type. Projective morphisms are proper; but the converse is not in general true. See also complete variety. A deep property of proper morphisms is the existence of a Stein factorization, namely the existence of an intermediate scheme such that a morphism can be expressed as one with connected fibres, followed by a finite morphism.
is finite if 
may be covered by affine open sets 
such that each 
is affine—say of the form 
-- and furthermore 
is finitely generated as a 
-module. See finite morphism.
The morphism
is locally of finite type if 
may be covered by affine open sets 
such that each inverse image 
is covered by affine open sets 
where each 
is finitely generated as a 
-algebra.
The morphism
is finite type if 
may be covered by affine open sets 
such that each inverse image 
is covered by finitely many affine open sets 
where each 
is finitely generated as a 
-algebra.
The morphism
has finite fibers if the fiber over each point 
is a finite set. A morphism is quasi-finite
if it is of finite type and has finite fibers.
Finite morphisms are quasi-finite, but not all morphisms having finite fibers are quasi-finite, and morphisms of finite type are usually not quasi-finite.
If x is a point of X, then the morphism f is of finite presentation at x (or finitely presented at x) if there is an open affine subset V of Y and an open affine neighbourhood U of x such that f(U) ⊆ V and
is a finitely presented algebra over 
. The morphism f is locally of finite presentation if it is finitely presented at all points of X. If Y is locally Noetherian, then f is locally of finite presentation if, and only if, it is locally of finite type.
The morphism f is of finite presentation (or X is finitely presented over Y) if it is locally of finite presentation, quasi-compact, and quasi-separated. If Y is locally Noetherian, then f is of finite presentation if, and only if, it is of finite type.
is flat
if it gives rise to a flat map
on stalks. When viewing a morphism as a family of schemes parametrized by the points of
, the geometric meaning of flatness could roughly be described by saying that the fibers 
do not vary too wildly.
in 
, consider the corresponding morphism of local rings
Let
be the maximal ideal of 
, and let
be the ideal generated by the image of
in 
. The morphism 
is unramified if it is locally of finite presentation and if for all 
in 
, 
is the maximal ideal of 
and the induced map
is a finite, separable field extension. This is the geometric version (and generalization) of an unramified field extension
in algebraic number theory
.
A morphism
is étale
if it is flat and unramified. There are several other equivalent definitions. In the case of smooth varieties
and 
over an algebraically closed field
, étale morphisms are precisely those inducing an isomorphism of tangent spaces
, which coincides with the usual notion of étale map in differential geometry.
Étale morphisms form a very important class of morphisms; they are used to build the so-called étale topology
and consequently the étale cohomology
, which is nowadays one of the cornerstones of algebraic geometry.
:
This notion is distinct for that of the usual set-theoretic image of f, f(Y). For example, the underlying space of Z always contain (but not necessarily equals) the Zariski closure of f(Y) in X, so if Y is any open (and not closed) subscheme of X and f is the inclusion map, then Z is different from f(Y). When Y is reduced, then Z is the Zariski closure of f(Y) endowed with the structure of reduced closed subscheme. But in general, unless f is quasi-compact, the construction of Z is not local on X.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, see affine scheme, projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
and scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
. The concern here is to list the fundamental technical definitions and properties of scheme theory. See also list of algebraic geometry topics.
Points
A scheme is a locally ringed space, so a fortiori a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, but the meanings of point of
are threefold:- a point
of the underlying topological space; - a
-valued point of 
is a morphism from 
to 
, for any scheme 
; - a geometric point, where
is defined over (is equipped with a morphism to) 
, where 
is a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, is a morphism from
to 
where 
is an algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of
.
Geometric points are what in the most classical cases, for example algebraic varieties that are complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s, would be the ordinary-sense points. The points
of the underlying space include analogues of the generic pointGeneric point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
s (in the sense of Zariski, not that of André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
), which specialise to ordinary-sense points. The
-valued points are thought of, via Yoneda's lemma, as a way of identifying with the representable functorRepresentable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
it sets up. Historically there was a process by which projective geometryProjective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
added more points (e.g. complex points, line at infinity
Line at infinity
In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...
) to simplify the geometry by refining the basic objects. The
-valued points were a massive further step.As part of the predominating Grothendieck approach
Grothendieck's relative point of view
Grothendieck's relative point of view is a heuristic applied in certain abstract mathematical situations, with a rough meaning of taking for consideration families of 'objects' explicitly depending on parameters, as the basic field of study, rather than a single such object...
, there are three corresponding notions of fiber of a morphism: the first being the simple inverse image of a point. The other two are formed by creating fiber products of two morphisms. For example, a geometric fiber of a morphism
is thought of as.This makes the extension from affine schemes, where it is just the tensor product of R-algebras, to all schemes of the fiber product operation a significant (if technically anodyne) result.
Properties of schemes
Most important properties of schemes are local in nature, i.e. a scheme X has a certain property P if and only if for any cover of X by open subschemes Xi, i.e. X= Xi, every Xi has the property P. It is usually the case that is enough to check one cover, not all possible ones. One also says that a certain property is Zariski-local, if one needs to distinguish between the Zariski topologyZariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
and other possible topologies, like the étale topology
Étale topology
In algebraic geometry, the étale topology is a Grothendieck topology on the category of schemes which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic...
.
Consider a scheme X and a cover by affine open subschemes Spec Ai. Using the dictionary between (commutative) rings
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
and affine schemes local properties are thus properties of the rings Ai. A property P is local in the above sense, iff the corresponding property of rings is stable under localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
.
For example, we can speak of locally Noetherian schemes, namely those which are covered by the spectra of Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
s. The fact that localizations of a Noetherian ring are still noetherian then means that the property of a scheme of being locally Noetherian is local in the above sense (whence the name). Another example: if a ring is reduced
Reduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
(i.e., has no non-zero nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
elements), then so are its localizations.
An example for a non-local property is separatedness (see below for the definition). Any affine scheme is separated, therefore any scheme is locally separated. However, the affine pieces may glue together pathologically to yield a non-separated scheme.
The following is a (non-exhaustive) list of local properties of rings, which are applied to schemes. Let X =
Spec Ai be a covering of a scheme by open affine subschemes. For definiteness, let k denote a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
in the following. Most of the examples also work with the integers Z as a base, though, or even more general bases.
| notion | definition | example | non-example |
|---|---|---|---|
| related to scheme structure | |||
| connected | The scheme is connected Connected space In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces... as a topological space. Since the connected components refine the irreducible component Irreducible component In mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :... s any irreducible scheme is connected but not vice versa. An affine scheme Spec(R) is connected iff IFF IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders... the ring R possesses no idempotents other than 0 and 1; such a ring is also called a connected ring. |
affine space Affine space In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point... , projective space Projective space In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively.... |
Spec(k[x]×k[x]) |
| irreducible | A scheme X is said to be irreducible Hyperconnected space In mathematics, a hyperconnected space is a topological space X that cannot be written as the union of two proper closed sets. The name irreducible space is preferred in algebraic geometry.... when (as a topological space) it is not the union of two closed subsets except if one is equal to X. Using the correspondence of prime ideals and points in an affine scheme, this means X is irreducible iff IFF IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders... X is connected and the rings Ai all have exactly one minimal prime ideal Prime ideal In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers... . (Rings possessing exactly one minimal prime ideal are therefore also called irreducible Irreducible ring In mathematics, especially in the field of commutative algebra, an irreducible ring is a commutative ring A that satisfies one of the following equivalent conditions:* A possesses exactly one minimal prime ideal;... .) Any noetherian scheme can be written uniquely as the union of finitely many maximal irreducible non-empty closed subsets, called its irreducible component Irreducible component In mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :... s. |
affine space Affine space In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point... , projective space Projective space In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively.... |
Spec k[x,y]/(xy) =  |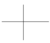
| reduced | The Ai are reduced ring Reduced ring In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0... s. Equivalently, none of its rings of sections  (U any open subset of X) has any nonzero nilpotent element. Allowing non-reduced schemes is one of the major generalizations from varieties to schemes. |
varieties Algebraic variety In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry... (by definition) |
Spec k[x]/(x2) |
| integral | A scheme that is both reduced and irreducible is called integral. Equivalently, a connected scheme that is covered by the spectra of integral domains. (Strictly speaking, this is not a local property, because the disjoint union Disjoint union In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union... of two integral schemes is not integral. However, for irreducible schemes, it is a local property.) |
Spec k[t]/f, f irreducible polynomial Irreducible polynomial In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization.... |
Spec A ⊕ B. (A, B ≠ 0) |
| normal | An integral scheme is called normal Normal scheme In mathematics, in the field of algebraic geometry, a normal scheme is a scheme X for which every stalk of its structure sheaf OX is an integrally closed local ring; that is, each stalk is an integral domain such that its integral closure in its field of fractions is equal to itself.Any reduced... , if the Ai are integrally closed Integrally closed In mathematics, more specifically in abstract algebra, the concept of integrally closed has two meanings, one for groups and one for rings. -Commutative rings:... domains. |
regular schemes | singular curves |
| related to regularity | |||
| regular | The Ai are regular Regular ring In commutative algebra, a regular ring is a commutative noetherian ring, such that the localization at every prime ideal is a regular local ring: that is, every such localization has the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension.Jean-Pierre... . |
smooth varieties over a field | Spec k[x,y]/(x2+x3-y2)= |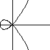
| Cohen-Macaulay | All local rings are Cohen-Macaulay Cohen-Macaulay ring In mathematics, a Cohen–Macaulay ring is a particular type of commutative ring, possessing some of the algebraic-geometric properties of a nonsingular variety, such as local equidimensionality.... . |
regular schemes, Spec k[x,y]/(xy) |  |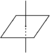
| related to "size" | |||
| locally noetherian | The Ai are Noetherian Noetherian ring In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element... rings. If in addition a finite number of such affine spectra covers X, the scheme is called noetherian. While it is true that the spectrum of a noetherian ring is a noetherian topological space Noetherian topological space In mathematics, a Noetherian topological space is a topological space in which closed subsets satisfy the descending chain condition. Equivalently, we could say that the open subsets satisfy the ascending chain condition, since they are the complements of the closed subsets... , the converse is false. |
(Virtually everything in algebraic geometry). |  |
| dimension | The dimension Krull dimension In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring.... , by definition the maximal length of a chain of irreducible closed subschemes, is a global property. It can be seen locally if a scheme is irreducible. It depends only on the topology, not on the structure sheaf. See also Global dimension Global dimension In ring theory and homological algebra, the global dimension of a ring A denoted gl dim A, is a non-negative integer or infinity which is a homological invariant of the ring. It is defined to be the supremum of the set of projective dimensions of all A-modules... . |
equidimensional scheme Equidimensional scheme In algebraic geometry, a field of mathematics, an equidimensional scheme is a scheme all of whose irreducible components are of the same dimension. All irreducible schemes are equidimensional. In affine space, the union of a line and a point not on the line is not equidimensional... s in dimension 0: Artinian Artinian ring In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are... schemes, 1: algebraic curves, 2: algebraic surfaces. |
|
| catenary | A scheme is catenary, if all chains between two irreducible closed subschemes have the same length. | (Virtually everything, e.g. varieties over a field) | |
Properties of scheme morphisms
One of Grothendieck's fundamental ideas is to emphasize relative notions, i.e. conditions on morphisms rather than conditions on schemes themselves. The category of schemes has a final object, the spectrum of the ring of integers; so that any scheme is over , and in a unique way.For the following definitions, we take as standard notation
to be a morphism of schemes. Parallel to the properties of schemes above, the following properties of morphisms are also of local nature, i.e. if there is an open covering of
by some open subschemes , such that the restriction of to has the property, then has it, as well.Notions related to the topological structure
A morphism of schemes is called open (closed) , if the underlying map of topological spaces is open (closed, respectively), i.e. if open subschemes of Y are mapped to open subschemes of X (and similarly for closed). For example, finitely presented flat morphisms are open and proper maps are closed.A morphism is called dominant, if the image f(Y) is dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
. A morphism of affine schemes Spec A → Spec B is dense if and only if the kernel of the corresponding map B → A is contained in the nilradical of A.
A morphism is called quasi-compact, if for some (equivalently: every) open affine cover of X by some Ui = Spec Bi, the preimages f−1(Ui) are quasi-compact.
Open and closed subschemes and immersions
An open subscheme of a scheme X is an open subset U with structure sheaf.Closed subschemes of a scheme X are defined to be those occurring in the following construction. Let J be a quasi-coherent sheaf of
-ideals. The support of the quotient sheaf is a closed subset Z of X and is a scheme called the closed subscheme defined by the quasi-coherent sheaf of ideals J. The reason the definition of closed subschemes relies on such a construction is that, unlike open subsets, a closed subset of a scheme does not have a unique structure as a subscheme.A subscheme, without qualifier, of X is a closed subscheme of an open subscheme of X.
Immersions are maps that factor through isomorphisms with subschemes. Specifically, an open immersion factors through an isomorphism with an open subscheme and a closed immersion factors through an isomorphism with a closed subscheme. Equivalently, f is a closed immersion if, and only if, it induces a homeomorphism from the underlying topological space of Y to a closed subset of the underlying topological space of X, and if the morphism
is surjective. A composition of immersions is again an immersion.Some authors, such as Hartshorne in his book Algebraic Geometry and Q. Liu in his book Algebraic Geometry and Arithmetic Curves, define immersions as the composite of an open immersion followed by a closed immersion. These immersions are immersions in the sense above, but the converse is false. Furthermore, under this definition, the composite of two immersions is not necessarily an immersion. However, the two definitions are equivalent when f is quasi-compact.
Note that an open immersion is completely described by its image in the sense of topological spaces, while a closed immersion is not:
and may be homeomorphic but not isomorphic. This happens, for example, if I is the radical of J but J is not a radical ideal. When specifying a closed subset of a scheme without mentioning the scheme structure, usually the so-called reduced scheme structure is meant, that is, the scheme structure corresponding to the unique radical ideal consisting of all functions vanishing on that closed subset.Affine and projective morphisms
A morphism is called affine if the preimage of any open affine subset is again affine. In more fancy terms, affine morphisms are defined by the global Spec construction for sheaves of OX-Algebras, defined by analogy with the spectrum of a ringSpectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
. Important affine morphisms are vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s, and finite morphisms.
Projective morphisms are defined similarly, but in practice they turn out to be more important than affine morphisms:
is called projective if it factors as a closed immersion followed by the projection of a projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
to . Again, one may say, that is projective if it is given by the global Proj construction on graded commutative OX-Algebras.Separated and proper morphisms
A separated morphism is a morphism such that the fiber product of with itself along has its diagonalDiagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
as a closed subscheme — in other words, the diagonal map is a closed immersion.
As a consequence, a scheme
is separated when the diagonal of within the scheme product of with itself is a closed immersion. Emphasizing the relative point of view, one might equivalently define a scheme to be separated if the unique morphism is separated.Notice that for a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
Y is Hausdorff iff the diagonal embedding
is closed. In algebraic geometry, the above formulation is used because a scheme is a Hausdorff space if and only if it is zero-dimensional. The difference between the topological and algebro-geometric context comes from the topological structure of the fiber product (in the category of schemes)
, which is different from the product of topological spaces.Any affine scheme Spec A is separated, because the diagonal corresponds to the surjective map of rings (hence is a closed immersion of schemes):
.A morphism is called quasi-separated or (X is quasi-separated over Y) if the diagonal morphism is quasi-compact. A scheme X is called quasi-separated if X is quasi-separated over Spec(Z).
While the separatedness is of rather technical nature, properness has deep geometrical meaning.
A morphism is proper if it is separated, universally closed (i.e. such that fiber products with it preserve closed immersions), and of finite type. Projective morphisms are proper; but the converse is not in general true. See also complete variety. A deep property of proper morphisms is the existence of a Stein factorization, namely the existence of an intermediate scheme such that a morphism can be expressed as one with connected fibres, followed by a finite morphism.
Finite, quasi-finite, finite type, and finite presentation morphisms
A morphism is finite if may be covered by affine open sets such that each is affine—say of the form -- and furthermore is finitely generated as a -module. See finite morphism.The morphism
is locally of finite type if may be covered by affine open sets such that each inverse image is covered by affine open sets where each is finitely generated as a -algebra.The morphism
is finite type if may be covered by affine open sets such that each inverse image is covered by finitely many affine open sets where each is finitely generated as a -algebra.The morphism
has finite fibers if the fiber over each point is a finite set. A morphism is quasi-finiteQuasi-finite morphism
In algebraic geometry, a branch of mathematics, a morphism f : X → Y of schemes is quasi-finite if it is finite type and satisfies any of the following equivalent conditions:...
if it is of finite type and has finite fibers.
Finite morphisms are quasi-finite, but not all morphisms having finite fibers are quasi-finite, and morphisms of finite type are usually not quasi-finite.
If x is a point of X, then the morphism f is of finite presentation at x (or finitely presented at x) if there is an open affine subset V of Y and an open affine neighbourhood U of x such that f(U) ⊆ V and
is a finitely presented algebra over . The morphism f is locally of finite presentation if it is finitely presented at all points of X. If Y is locally Noetherian, then f is locally of finite presentation if, and only if, it is locally of finite type.The morphism f is of finite presentation (or X is finitely presented over Y) if it is locally of finite presentation, quasi-compact, and quasi-separated. If Y is locally Noetherian, then f is of finite presentation if, and only if, it is of finite type.
Flat morphisms
A morphism is flatFlat morphism
In mathematics, in particular in the theory of schemes in algebraic geometry, a flat morphism f from a scheme X to a scheme Y is a morphism such that the induced map on every stalk is a flat map of rings, i.e.,is a flat map for all P in X...
if it gives rise to a flat map
Flat map
The flat map in differential geometry is a name for the mapping that converts coordinate basis vectors into corresponding coordinate 1-forms.A flat map in ring theory is a homomorphism f from a ring R to a ring S such that S is a flat R-module, where the action of R on S is given by f....
on stalks. When viewing a morphism as a family of schemes parametrized by the points of
, the geometric meaning of flatness could roughly be described by saying that the fibers do not vary too wildly.Unramified and étale morphisms
For a point in , consider the corresponding morphism of local rings
Let
be the maximal ideal of , and let
be the ideal generated by the image of
in . The morphism is unramified if it is locally of finite presentation and if for all in , is the maximal ideal of and the induced mapis a finite, separable field extension. This is the geometric version (and generalization) of an unramified field extension
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
in algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.
A morphism
is étaleÉtale morphism
In algebraic geometry, a field of mathematics, an étale morphism is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem, but because open sets in the Zariski topology are so large, they are not...
if it is flat and unramified. There are several other equivalent definitions. In the case of smooth varieties
and over an algebraically closed fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, étale morphisms are precisely those inducing an isomorphism of tangent spaces
, which coincides with the usual notion of étale map in differential geometry.Étale morphisms form a very important class of morphisms; they are used to build the so-called étale topology
Étale topology
In algebraic geometry, the étale topology is a Grothendieck topology on the category of schemes which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic...
and consequently the étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
, which is nowadays one of the cornerstones of algebraic geometry.
Smooth morphisms
The higher-dimensional analog of étale morphisms are smooth morphisms. There are many different characterisations of smoothness. The following are equivalent definitions of smoothness:- 1) for any y ∈ Y, there are open affine neighborhoods V and U of y, x=f(y), respectively, such that the restriction of f to V factors as an étale morphism followed by the projection of affine n-spaceAffine spaceIn mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
over U. - 2) f is flat, locally of finite presentation, and for every geometric point
of Y (a morphism from the spectrum of an algebraically closed field 
to Y), the geometric fiber 
is a smooth n-dimensional variety over 
in the sense of classical algebraic geometry.
Scheme-theoretic image
If is any morphism of schemes, the scheme-theoretic image of f is the unique closed subscheme which satisfies the following universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
:
- f factors through i,
- if is any closed subscheme of X such that f factors through j, then i also factors through j.
This notion is distinct for that of the usual set-theoretic image of f, f(Y). For example, the underlying space of Z always contain (but not necessarily equals) the Zariski closure of f(Y) in X, so if Y is any open (and not closed) subscheme of X and f is the inclusion map, then Z is different from f(Y). When Y is reduced, then Z is the Zariski closure of f(Y) endowed with the structure of reduced closed subscheme. But in general, unless f is quasi-compact, the construction of Z is not local on X.