Noetherian topological space
Encyclopedia
In mathematics
, a Noetherian topological space is a topological space
in which closed subsets satisfy the descending chain condition. Equivalently, we could say that the open subsets satisfy the ascending chain condition
, since they are the complements of the closed subsets. It can also be shown to be equivalent that every open subset of such a space is compact
, and in fact the seemingly stronger statement that every subset is compact.
is called Noetherian if it satisfies the descending chain condition for closed subsets: for any sequence
of closed subsets
of 
, there is an integer
such that 
condition:
, where for the Zariski topology
an irreducible set has the intuitive property that any closed proper subset has smaller dimension. Since dimension can only 'jump down' a finite number of times, and algebraic set
s are made up of finite unions of irreducible sets, descending chains of Zariski closed sets must eventually be constant.
A more algebraic way to see this is that the associated ideals
defining algebraic sets must satisfy the ascending chain condition
. That follows because the rings of algebraic geometry, in the classical sense, are Noetherian ring
s. This class of examples therefore also explains the name.
If R is a commutative Noetherian ring, then Spec(R), the prime spectrum of R, is a Noetherian topological space.
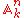(affine 
-space over a field
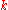) under the Zariski topology
is an example of a Noetherian topological space. By properties of the ideal of a subset of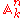
, we know that if
is a descending chain of Zariski-closed subsets, then
is an ascending chain of ideals of
Since 
is a Noetherian ring, there exists an integer 
such that
But because we have a one-to-one
correspondence between radical ideals
of
and Zariski-closed sets in 
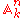we have 
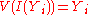for all 
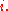Hence
as required.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Noetherian topological space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
in which closed subsets satisfy the descending chain condition. Equivalently, we could say that the open subsets satisfy the ascending chain condition
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
, since they are the complements of the closed subsets. It can also be shown to be equivalent that every open subset of such a space is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, and in fact the seemingly stronger statement that every subset is compact.
Definition
A topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is called Noetherian if it satisfies the descending chain condition for closed subsets: for any sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of closed subsets
of , there is an integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
such that Relation to compactness
The Noetherian condition can be seen as a strong compactnessCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
condition:
- Every Noetherian topological space is compact.
- A topological space
is Noetherian if and only if every subspaceSubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
of
is compact. (i.e. 
is hereditarily compact).
Noetherian topological spaces from algebraic geometry
Many examples of Noetherian topological spaces come from algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, where for the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
an irreducible set has the intuitive property that any closed proper subset has smaller dimension. Since dimension can only 'jump down' a finite number of times, and algebraic set
Algebraic set
In mathematics, an algebraic set over an algebraically closed field K is the set of solutions in Kn of a set of simultaneous equationsand so on up to...
s are made up of finite unions of irreducible sets, descending chains of Zariski closed sets must eventually be constant.
A more algebraic way to see this is that the associated ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
defining algebraic sets must satisfy the ascending chain condition
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
. That follows because the rings of algebraic geometry, in the classical sense, are Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
s. This class of examples therefore also explains the name.
If R is a commutative Noetherian ring, then Spec(R), the prime spectrum of R, is a Noetherian topological space.
Example
The space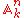 (affine -space over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
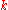) under the Zariski topologyZariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
is an example of a Noetherian topological space. By properties of the ideal of a subset of
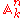, we know that ifis a descending chain of Zariski-closed subsets, then
is an ascending chain of ideals of
Since is a Noetherian ring, there exists an integer such thatBut because we have a one-to-one
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
correspondence between radical ideals
Radical of an ideal
In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
of
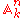and Zariski-closed sets in we have 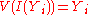for all 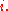Hence as required.