Algebraic set
Encyclopedia
In mathematics
, an algebraic set over an algebraically closed field
K is the set of solutions in Kn (n-tuples of elements of K) of a set of simultaneous equations
and so on up to
for some integer m, where the Pi are polynomials over K. That is, we consider the simultaneous solution set of these equations applied to vectors
with the xi taken from K.
Algebraic sets are the primitive objects of algebraic geometry
. There is a satisfactory definition of dimension
.
One could define similarly the algebraic sets over an arbitrary field K. But then such sets can be empty set
s, while the same equations can have numerous solutions in an algebraic closure
of K. A more reasonable definition is to consider the solutions in 
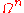of equations with coefficients in K.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an algebraic set over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
K is the set of solutions in Kn (n-tuples of elements of K) of a set of simultaneous equations
Simultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
- P1(X1, ...,Xn) = 0
- P2(X1, ...,Xn) = 0
and so on up to
- Pm(X1, ...,Xn) = 0
for some integer m, where the Pi are polynomials over K. That is, we consider the simultaneous solution set of these equations applied to vectors
with the xi taken from K.
Algebraic sets are the primitive objects of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. There is a satisfactory definition of dimension
Dimension of an algebraic variety
In mathematics, the dimension of an algebraic variety V in algebraic geometry is defined, informally speaking, as the number of independent rational functions that exist on V.For example, an algebraic curve has by definition dimension 1...
.
One could define similarly the algebraic sets over an arbitrary field K. But then such sets can be empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
s, while the same equations can have numerous solutions in an algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of K. A more reasonable definition is to consider the solutions in 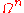of equations with coefficients in K.