
Ascending chain condition
Encyclopedia
The ascending chain condition (ACC) and descending chain condition (DCC) are finiteness properties satisfied by some algebraic structures, most importantly, ideal
s in certain commutative ring
s. These conditions played an important role in the development of the structure theory of commutative rings in the works of David Hilbert
, Emmy Noether
, and Emil Artin
.
The conditions themselves can be stated in an abstract form, so that they make sense for any partially ordered set
. This point of view is useful in abstract algebraic dimension theory due to Gabriel and Rentschler.
(poset) P is said to satisfy the ascending chain condition (ACC) if every ascending chain of elements eventually terminates. Equivalently, given any sequence of elements of P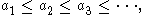
there exists a positive integer
n such that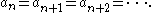
Similarly, P is said to satisfy the descending chain condition (DCC) if every descending chain of elements eventually terminates, or equivalently if any descending sequence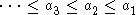
of elements of P eventually stabilizes (that is, there is no infinite descending chain
).
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
s in certain commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s. These conditions played an important role in the development of the structure theory of commutative rings in the works of David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
, and Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
.
The conditions themselves can be stated in an abstract form, so that they make sense for any partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
. This point of view is useful in abstract algebraic dimension theory due to Gabriel and Rentschler.
Definition
A partially ordered setPartially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
(poset) P is said to satisfy the ascending chain condition (ACC) if every ascending chain of elements eventually terminates. Equivalently, given any sequence of elements of P
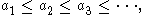
there exists a positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n such that
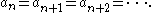
Similarly, P is said to satisfy the descending chain condition (DCC) if every descending chain of elements eventually terminates, or equivalently if any descending sequence
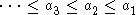
of elements of P eventually stabilizes (that is, there is no infinite descending chain
Infinite descending chain
Given a set S with a partial order ≤, an infinite descending chain is a chain V that is a subset of S upon which ≤ defines a total order such that V has no least element, that is, an element m such that for all elements n in V it holds that m ≤ n.As an example, in the set of integers, the chain...
).
Comments
- A subtly different and stronger condition than "containing no infinite ascending/descending chains" is "contains no arbitrarily long ascending/descending chains (optionally, 'based at a given element')". For instance, the disjoint union of the posets {0}, {0,1}, {0,1,2}, etc., satisfies both the ACC and the DCC, but has arbitrarily long chains. If one further identifies the 0 in all of these sets, then every chain is finite, but there are arbitrarily long chains based at 0.
- The descending chain condition on P is equivalent to P being well-founded: every nonempty subset of P has a minimal element (also called the minimal condition).
- Similarly, the ascending chain condition is equivalent to P being converse well-founded: every nonempty subset of P has a maximal element (the maximal condition).
- Every finite poset satisfies both ACC and DCC.
- A totally ordered setTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
that satisfies the descending chain condition is called a well-ordered setWell-orderIn mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
.
See also
- ArtinianArtinianIn mathematics, Artinian, named for Emil Artin, is an adjective that describes objects that satisfy particular cases of the descending chain condition.*A ring is an Artinian ring if it satisfies the descending chain condition on ideals...
- NoetherianNoetherianIn mathematics, the adjective Noetherian is used to describe objects that satisfy an ascending or descending chain condition on certain kinds of subobjects; in particular,* Noetherian group, a group that satisfies the ascending chain condition on subgroups...
- Krull dimensionKrull dimensionIn commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
- Ascending chain condition for principal ideals

