Normal scheme
Encyclopedia
In mathematics
, in the field of algebraic geometry
, a normal scheme is a scheme
X for which every stalk (local ring)
of its structure sheaf OX is an integrally closed
local ring
; that is, each stalk is an integral domain such that its integral closure in its field of fractions
is equal to itself.
Any reduced scheme has a normalization, whose construction we first give for irreducible reduced schemes.
An irreducible and reduced scheme
has the property that every affine chart is a domain. Choose an affine cover corresponding to rings 
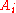. Compute the integral closure of each of these in its fraction field, denote them by 
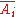. It is not hard to see that one can construct a new scheme 
by gluing together the affine schemes Spec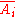
.
If the initial scheme is not irreducible, one can define the normalization as the disjoint union of the normalizations of the irreducible components. An alternate, equivalent, definition uses integral closures in rings of fractions where any nonzero divisor is allowed in the denominator.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a normal scheme is a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
X for which every stalk (local ring)
- OX,x
of its structure sheaf OX is an integrally closed
Integrally closed domain
In commutative algebra, an integrally closed domain A is an integral domain whose integral closure in the field of fractions of A is A itself...
local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
; that is, each stalk is an integral domain such that its integral closure in its field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
is equal to itself.
Any reduced scheme has a normalization, whose construction we first give for irreducible reduced schemes.
An irreducible and reduced scheme
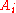has the property that every affine chart is a domain. Choose an affine cover corresponding to rings . Compute the integral closure of each of these in its fraction field, denote them by 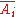. It is not hard to see that one can construct a new scheme by gluing together the affine schemes Spec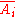.If the initial scheme is not irreducible, one can define the normalization as the disjoint union of the normalizations of the irreducible components. An alternate, equivalent, definition uses integral closures in rings of fractions where any nonzero divisor is allowed in the denominator.