Tensor product of modules
Encyclopedia
In mathematics
, the tensor product of modules is a construction that allows arguments about bilinear maps (roughly speaking, "multiplication") to be carried out in terms of linear maps (module homomorphisms). The module construction is analogous to the construction of the tensor product
of vector space
s, but can be carried out for a pair of modules
over a commutative ring
resulting in a third module, and also for a pair of a left-module and a right-module over any ring
, with result an abelian group
. Tensor products are important in areas of abstract algebra
, homological algebra
, algebraic topology
and algebraic geometry
. The universal property
of the tensor product of vector spaces extends to more general situations in abstract algebra. It allows the study of bilinear or multilinear operations via linear operations. The tensor product of an algebra and a module can be used for extension of scalars
. For a commutative ring, the tensor product of modules can be iterated to form the tensor algebra
of a module, allowing one to define multiplication in the module in a universal way.
The set of all such bilinear maps from M × N to Z is denoted by Bilin(M,N;Z).
Property 3 differs slightly from the definition for vector spaces. This is necessary because Z is only assumed to be an abelian group, so r·φ(m,n) would not make sense.
If φ, ψ are bilinear maps, then φ + ψ is a bilinear map, and -φ is a bilinear map, when these operations are defined pointwisely
. This turns the set Bilin(M,N;Z) into an abelian group. The neutral element is the zero mapping.
For M and N fixed, the map Z ↦ Bilin(M,N;Z) is a functor
from the category of abelian groups
to the category of sets
. The morphism part is given by mapping a group homomorphism g : Z → Z′ to the function [φ ↦ g ∘ φ], which goes from Bilin(M,N;Z) to Bilin(M,N;Z′).
is an abelian group
together with a bilinear map (in the sense defined above)
which is universal
in the following sense:
As with all universal properties, the above property defines the tensor product uniquely up to
a unique isomorphism: any other object and bilinear map with the same properties will be isomorphic to M⊗RN and ⊗. The definition does not prove the existence of M⊗RN; see below for a construction.
The tensor product can also be defined as a representing object
for the functor Z → BilinR(M,N;Z). This is equivalent to the universal mapping property given above.
Strictly speaking, the ring used to form the tensor should be indicated: most modules can be considered as modules over several different rings or over the same ring with a different actions of the ring on the module elements. For example, it can be shown that R⊗RR and R⊗ZR are completely different from each other. However in practice, whenever the ring is clear from context, the subscript denoting the ring may be dropped.
s Q and the integers modulo n
Zn. As with any abelian group, both can be considered as modules over the integer
s, Z.
Let B: Q × Zn → M be a Z-bilinear operator. Then B(q, k) = B(q/n, nk) = B(q/n, 0) = 0, so every bilinear operator is identically zero. Therefore, if we define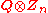
to be the trivial module, and 
to be the zero bilinear function, then we see that the properties for the tensor product are satisfied. Therefore, the tensor product of Q and Zn is {0}.
with basis the symbols m ⊗ n for m in M and n in N by the subgroup generated by all elements of the form
where m,m′ in M, n,n′ in N, and r in R. The function which takes (m,n) to the coset containing m ⊗ n is bilinear, and the subgroup has been chosen minimally so that this map is bilinear.
The direct product
of M and N is rarely isomorphic to the tensor product of M and N. When R is not commutative, then the tensor product requires that M and N be modules on opposite sides, while the direct product requires they be modules on the same side. In all cases the only function from M × N to Z which is both linear and bilinear is the zero map.
is a bifunctor which accepts a right and a left R module pair as input, and assigns them to the tensor product in the category of abelian groups
.
By fixing a right R module M, a functor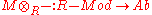
arises, and symmetrically a left R module N could be fixed to create a functor 
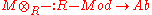. Unlike the Hom bifunctor 
, the tensor functor is covariant in both inputs.
It can be shown that M⊗- and -⊗N are always right exact functors, but not necessarily left exact. By definition, a module T is a flat module
if T⊗- is an exact functor.
If {mi}i∈I and {nj}j∈J are generating sets for M and N, respectively, then {mi⊗nj}i∈I,j∈J will be a generating set for M⊗N. Because the tensor functor M⊗R- sometimes fails to be left exact, this may not be a minimal generating set, even if the original generating sets are minimal.
When the tensor products are taken over a field F so that -⊗- is exact in both positions, and the generating sets are bases of M and N, it is true that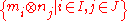
indeed forms a basis for M⊗F N.
is that every trilinear map on
corresponds to a unique linear map
The binary tensor product is associative: (M1 ⊗ M2) ⊗ M3 is naturally isomorphic to M1 ⊗ (M2 ⊗ M3). The tensor product of three modules defined by the universal property of trilinear maps is isomorphic to both of these iterated tensor products.
, then M⊗RN can be made into a left S-module using the obvious operation s(m⊗n)=(sm⊗n). Similarly, if N is an (R,T)-bimodule, then M⊗RN is a right T-module using the operation (m⊗n)t=(m⊗nt). If M and N each have bimodule structures as above, then M⊗RN is an (S,T)-bimodule. In the case where R is a commutative ring, all of its modules can be thought of as (R,R)-bimodules, and then M⊗RN can be made into an R-module as described. In the construction of the tensor product over a commutative ring R, the multiplication operation can either be defined a posteriori as just described, or can be built in from the start by forming the quotient of a free R-module by the submodule generated by the elements given above for the general construction, augmented by the elements r(m ⊗ n) − m ⊗ (r·n), or equivalently the elements (m·r) ⊗ n − r(m ⊗ n).
If {mi}i∈I and {nj}j∈J are generating sets for M and N, respectively, then {mi⊗nj}i∈I,j∈J will be a generating set for M⊗N. Because the tensor functor M⊗R- is right exact
, but sometimes not left exact, this may not be a minimal generating set, even if the original generating sets are minimal. If M is a flat module
, the functor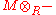
is exact by the very definition of a flat module. If the tensor products are taken over a field F, we are in the case of vector spaces as above. Since all F modules are flat, the bifunctor
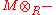is exact in both positions, and the two given generating sets are bases, then
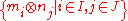indeed forms a basis for M ⊗F N.
If S and T are commutative R-algebras, then S ⊗R T will be a commutative R-algebra as well, with the multiplication map defined by (m1 ⊗ m2)(n1 ⊗ n2) = (m1n1 ⊗ m2n2) and extended by linearity. In this setting, the tensor product become a fibered coproduct in the category of R-algebras. Note that any ring is a Z-algebra, so we may always take M ⊗Z N.
If S1MR is an S1-R-bimodule, then there is a unique left S1-module structure on M⊗N which is compatible with the tensor map ⊗:M×N→M⊗RN. Similarly, if RNS2 is an R-S2-bimodule, then there is a unique right S2-module structure on M⊗RN which is compatible with the tensor map.
If M and N are both R-modules over a commutative ring, then their tensor product is again an R-module. If R is a ring, RM is a left R-module, and the commutator
of any two elements r and s of R is in the annihilator
of M, then we can make M into a right R module by setting
The action of R on M factors through an action of a quotient commutative ring. In this case the tensor product of M with itself over R is again an R-module. This is a very common technique in commutative algebra.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the tensor product of modules is a construction that allows arguments about bilinear maps (roughly speaking, "multiplication") to be carried out in terms of linear maps (module homomorphisms). The module construction is analogous to the construction of the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, but can be carried out for a pair of modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
resulting in a third module, and also for a pair of a left-module and a right-module over any ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, with result an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. Tensor products are important in areas of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. The universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
of the tensor product of vector spaces extends to more general situations in abstract algebra. It allows the study of bilinear or multilinear operations via linear operations. The tensor product of an algebra and a module can be used for extension of scalars
Extension of scalars
In abstract algebra, extension of scalars is a means of producing a module over a ring S from a module over another ring R, given a homomorphism f : R \to S between them...
. For a commutative ring, the tensor product of modules can be iterated to form the tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
of a module, allowing one to define multiplication in the module in a universal way.
Multilinear mappings
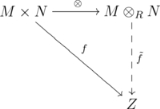
For a ring R, a right R-module MR, a left R-module RN, and an abelian group Z, a bilinear map or balanced product from M × N to Z is a function φ: M × N → Z such that for all m,m′ in M, n,n′ in N, and r in R:- φ(m+m′,n) = φ(m,n) + φ(m′,n)
- φ(m,n+n′) = φ(m,n) + φ(m,n′)
- φ(m·r,n) = φ(m,r·n)
The set of all such bilinear maps from M × N to Z is denoted by Bilin(M,N;Z).
Property 3 differs slightly from the definition for vector spaces. This is necessary because Z is only assumed to be an abelian group, so r·φ(m,n) would not make sense.
If φ, ψ are bilinear maps, then φ + ψ is a bilinear map, and -φ is a bilinear map, when these operations are defined pointwisely
Pointwise
In mathematics, the qualifier pointwise is used to indicate that a certain property is defined by considering each value f of some function f. An important class of pointwise concepts are the pointwise operations — operations defined on functions by applying the operations to function values...
. This turns the set Bilin(M,N;Z) into an abelian group. The neutral element is the zero mapping.
For M and N fixed, the map Z ↦ Bilin(M,N;Z) is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
to the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. The morphism part is given by mapping a group homomorphism g : Z → Z′ to the function [φ ↦ g ∘ φ], which goes from Bilin(M,N;Z) to Bilin(M,N;Z′).
Definition
Let M,N and R be as in the previous section. The tensor product over Ris an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
together with a bilinear map (in the sense defined above)
which is universal
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
in the following sense:
- For every abelian group Z and every bilinear map
- there is a unique group homomorphism
- such that
As with all universal properties, the above property defines the tensor product uniquely up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a unique isomorphism: any other object and bilinear map with the same properties will be isomorphic to M⊗RN and ⊗. The definition does not prove the existence of M⊗RN; see below for a construction.
The tensor product can also be defined as a representing object
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
for the functor Z → BilinR(M,N;Z). This is equivalent to the universal mapping property given above.
Strictly speaking, the ring used to form the tensor should be indicated: most modules can be considered as modules over several different rings or over the same ring with a different actions of the ring on the module elements. For example, it can be shown that R⊗RR and R⊗ZR are completely different from each other. However in practice, whenever the ring is clear from context, the subscript denoting the ring may be dropped.
Examples
Consider the rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q and the integers modulo n
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
Zn. As with any abelian group, both can be considered as modules over the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, Z.
Let B: Q × Zn → M be a Z-bilinear operator. Then B(q, k) = B(q/n, nk) = B(q/n, 0) = 0, so every bilinear operator is identically zero. Therefore, if we define
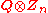to be the trivial module, and to be the zero bilinear function, then we see that the properties for the tensor product are satisfied. Therefore, the tensor product of Q and Zn is {0}.Construction
The construction of M ⊗ N takes a quotient of a free abelian groupFree abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
with basis the symbols m ⊗ n for m in M and n in N by the subgroup generated by all elements of the form
- −(m+m′) ⊗ n + m ⊗ n + m′ ⊗ n
- −m ⊗ (n+n′) + m ⊗ n + m ⊗ n′
- (m·r) ⊗ n − m ⊗ (r·n)
where m,m′ in M, n,n′ in N, and r in R. The function which takes (m,n) to the coset containing m ⊗ n is bilinear, and the subgroup has been chosen minimally so that this map is bilinear.
The direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of M and N is rarely isomorphic to the tensor product of M and N. When R is not commutative, then the tensor product requires that M and N be modules on opposite sides, while the direct product requires they be modules on the same side. In all cases the only function from M × N to Z which is both linear and bilinear is the zero map.
Relationship to flat modules
In general, is a bifunctor which accepts a right and a left R module pair as input, and assigns them to the tensor product in the category of abelian groupsCategory of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
.
By fixing a right R module M, a functor
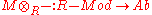arises, and symmetrically a left R module N could be fixed to create a functor 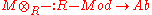. Unlike the Hom bifunctor , the tensor functor is covariant in both inputs.It can be shown that M⊗- and -⊗N are always right exact functors, but not necessarily left exact. By definition, a module T is a flat module
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
if T⊗- is an exact functor.
If {mi}i∈I and {nj}j∈J are generating sets for M and N, respectively, then {mi⊗nj}i∈I,j∈J will be a generating set for M⊗N. Because the tensor functor M⊗R- sometimes fails to be left exact, this may not be a minimal generating set, even if the original generating sets are minimal.
When the tensor products are taken over a field F so that -⊗- is exact in both positions, and the generating sets are bases of M and N, it is true that
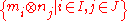indeed forms a basis for M⊗F N.Several modules
It is possible to generalize the definition to a tensor product of any number of spaces. For example, the universal property of- M1 ⊗ M2 ⊗ M3
is that every trilinear map on
- M1 × M2 × M3 → Z
corresponds to a unique linear map
- M1 ⊗ M2 ⊗ M3 → Z.
The binary tensor product is associative: (M1 ⊗ M2) ⊗ M3 is naturally isomorphic to M1 ⊗ (M2 ⊗ M3). The tensor product of three modules defined by the universal property of trilinear maps is isomorphic to both of these iterated tensor products.
Additional structure
The tensor product, as defined, is an abelian group, but in general, it does not immediately have an R-module structure. However, if M is an (S,R)-bimoduleBimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
, then M⊗RN can be made into a left S-module using the obvious operation s(m⊗n)=(sm⊗n). Similarly, if N is an (R,T)-bimodule, then M⊗RN is a right T-module using the operation (m⊗n)t=(m⊗nt). If M and N each have bimodule structures as above, then M⊗RN is an (S,T)-bimodule. In the case where R is a commutative ring, all of its modules can be thought of as (R,R)-bimodules, and then M⊗RN can be made into an R-module as described. In the construction of the tensor product over a commutative ring R, the multiplication operation can either be defined a posteriori as just described, or can be built in from the start by forming the quotient of a free R-module by the submodule generated by the elements given above for the general construction, augmented by the elements r(m ⊗ n) − m ⊗ (r·n), or equivalently the elements (m·r) ⊗ n − r(m ⊗ n).
If {mi}i∈I and {nj}j∈J are generating sets for M and N, respectively, then {mi⊗nj}i∈I,j∈J will be a generating set for M⊗N. Because the tensor functor M⊗R- is right exact
Exact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
, but sometimes not left exact, this may not be a minimal generating set, even if the original generating sets are minimal. If M is a flat module
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
, the functor
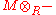is exact by the very definition of a flat module. If the tensor products are taken over a field F, we are in the case of vector spaces as above. Since all F modules are flat, the bifunctor 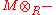is exact in both positions, and the two given generating sets are bases, then 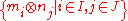indeed forms a basis for M ⊗F N.If S and T are commutative R-algebras, then S ⊗R T will be a commutative R-algebra as well, with the multiplication map defined by (m1 ⊗ m2)(n1 ⊗ n2) = (m1n1 ⊗ m2n2) and extended by linearity. In this setting, the tensor product become a fibered coproduct in the category of R-algebras. Note that any ring is a Z-algebra, so we may always take M ⊗Z N.
If S1MR is an S1-R-bimodule, then there is a unique left S1-module structure on M⊗N which is compatible with the tensor map ⊗:M×N→M⊗RN. Similarly, if RNS2 is an R-S2-bimodule, then there is a unique right S2-module structure on M⊗RN which is compatible with the tensor map.
If M and N are both R-modules over a commutative ring, then their tensor product is again an R-module. If R is a ring, RM is a left R-module, and the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
- rs − sr
of any two elements r and s of R is in the annihilator
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
of M, then we can make M into a right R module by setting
- mr = rm.
The action of R on M factors through an action of a quotient commutative ring. In this case the tensor product of M with itself over R is again an R-module. This is a very common technique in commutative algebra.