Pointwise
Encyclopedia
In mathematics
, the qualifier pointwise is used to indicate that a certain property is defined by considering each value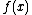
of some function 
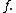An important class of pointwise concepts are the pointwise operations — operations defined on functions by applying the operations to function values separately for each point in the domain
of definition. Important relations
can also be defined pointwise.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the qualifier pointwise is used to indicate that a certain property is defined by considering each value
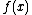of some function 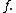An important class of pointwise concepts are the pointwise operations — operations defined on functions by applying the operations to function values separately for each point in the domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of definition. Important relations
Theory of relations
The theory of relations treats the subject matter of relations in its combinatorial aspect, as distinguished from, though related to, its more properly logical study on one side and its more generally mathematical study on another....
can also be defined pointwise.
Pointwise operations
Examples include-
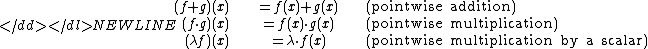
where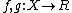
.
See pointwise productPointwise productThe pointwise product of two functions is another function, obtained by multiplying the image of the two functions at each value in the domain...
, scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
.
Pointwise operations inherit such properties as associativityAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, commutativityCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
and distributivityDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
from corresponding operations on the codomainCodomainIn mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
. An example of an operation on functions which is not pointwise is convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
.
By taking some algebraic structureAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
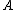in the place of 
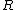, we can turn the set of all functions 
to the carrierCarrierCarrier may refer to:- Science :* Carrier wave, a waveform suitable for modulation by an information-bearing signal* Charge carrier, an unbound particle carrying an electric charge* a mathematical Set over which an algebraic structure is defined...
of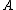
into an algebraic structure of the same type in an analogous way.
Componentwise operations
Componentwise operations are usually defined on vectors, where vectors are elements of the set
for some natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
and some fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. 
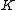can be generalized to a set. If we denote the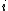 
-th component of any vector 
as 
, then componentwise addition is 
.
A tuple can be regarded as a function, and a vector is a tuple. Therefore any vector
corresponds to the function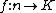 
such that 
, and any componentwise operation on vectors is the pointwise operation on functions corresponding to those vectors.
Pointwise relations
In order theoryOrder theoryOrder theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
it is common to define a pointwise partial order on functions. With A, B posets, the set of functions A → B can be ordered by f ≤ g if and only if (∀x ∈ A) f(x) ≤ g(x). Pointwise orders also inherit some properties of the underlying posets. For instance if A and B are continuous lattices, then so is the set of functions A → B with pointwise order. Using the pointwise order on functions one can concisely define other important notions, for instance:
- A closure operatorClosure operatorIn mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
c on a poset P is a monotoneMonotoneMonotone refers to a sound, for example speech or music, that has a single unvaried tone.Monotone or monotonicity may also refer to:*Monotone , an open source revision control system*Monotone class theorem, in measure theory...
and idempotent self-map on P (i.e. a projection operator) with the additional property that idA ≤ c, where id is the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
.
- Similarly, a projection operator k is called a kernel operator if and only if k ≤ idA.
An example of infinitary pointwise relation is pointwise convergencePointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
of functions — a sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of functions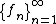
with
convergesLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
pointwise to a function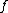
if for each 
in 
- A closure operator