Theory of relations
Encyclopedia
The theory of relations treats the subject matter of relations in its combinatorial aspect, as distinguished from, though related to, its more properly logical study on one side and its more generally mathematical study on another.
A relation, as conceived in the combinatorial theory of relations, is a mathematical object that in general can have a very complex type, the complexity of which is best approached in several stages, as indicated next.
In order to approach the combinatorial definition of a relation, it helps to introduce a few preliminary notions that can serve as stepping stones to the general idea.
A relation in mathematics is defined as an object that has its existence as such within a definite context or setting. It is literally the case that to change this setting is to change the relation that is being defined. The particular type of context that is needed here is formalized as a collection of elements from which are chosen the elements of the relation in question. This larger collection of elementary relations or tuple
s is constructed by means of the set-theoretic product commonly known as the cartesian product
.
In the special case of a finitary relation, for concreteness a k-place relation, the concepts of figure and ground are defined as follows:
Strictly speaking, then, the relation L consists of a couple of things, L = (F(L), G(L)), but it is customary in loose speech to use the single name L in a systematically equivocal fashion, taking it to denote either the couple L = (F(L), G(L)) or the figure F(L). There is usually no confusion about this so long as the ground of the relation can be gathered from context.
The formal definition simply repeats more concisely what was said above, merely unwrapping the conceptual packaging of the relation's ground to define the relation in 1 + k parts, as L = (F(X), X1, …, Xk), rather than just the two, as L = (F(L), G(L)).
A k-ary predicate is a boolean-valued function
on k variables.
Let L be a k-place relation L ⊆ X1 × … × Xk.
Select a relational domain Xj and one of its elements x. Then Lx.j is a subset of L that is referred to as the flag of L with x at j, or the x.j-flag of L, an object which has the following definition:
Any property C of the local flag Lx.j ⊆ L is said to be a local incidence property of L with respect to the locus x at j.
A k-adic relation L ⊆ X1 × … × Xk is said to be C-regular at j if and only if every flag of L with x at j has the property C, where x is taken to vary over the theme of the fixed domain Xj.
Expressed in symbols, L is C-regular at j if and only if C(Lx.j) is true for all x in Xj.
For example, L is said to be c-regular at j if and only if the cardinality of the local flag Lx.j is c for all x in Xj, or, to write it in symbols, if and only if |Lx.j| = c for all x in Xj.
In a similar fashion, one can define the NIPs (< c)-regular at j, (> c)-regular at j, and so on. For ease of reference, a few of these definitions are recorded here:
The definition of a local flag can be broadened from a point x in Xj to a subset M of Xj, arriving at the definition of a regional flag in the following way:
Suppose that L ⊆ X1 × … × Xk, and choose a subset M ⊆ Xj. Then LM.j is a subset of L that is said to be the flag of L with M at j, or the M.j-flag of L, an object which has the following definition:
Returning to 2-adic relations, it is useful to describe some familiar classes of objects in terms of their local and their numerical incidence properties. Let L ⊆ S × T be an arbitrary 2-adic relation. The following properties of L can be defined:
If L ⊆ S × T is tubular at S, then L is called a partial function or a prefunction from S to T, sometimes indicated by giving L an alternate name, say, "p", and writing L = p : S
T.
Just by way of formalizing the definition:
If L is a prefunction p : S
T that happens to be total at S, then L is called a function from S to T, indicated by writing L = f : S → T. To say that a relation L ⊆ S × T is totally tubular at S is to say that it is 1-regular at S. Thus, we may formalize the following definition:
In the case of a function f : S → T, one has the following additional definitions:
One dimension of variation is reflected in the names that are given to k-place relations, with some writers using medadic, monadic, dyadic, triadic, k-adic where other writers use nullary, unary, binary, ternary, k-ary.
One finds a relation on a finite number of domains described as either a finitary relation or a polyadic relation. If the number of domains is finite, say equal to k, then the parameter
k may be referred to as the arity
, the adicity, or the dimension
of the relation. In these cases, the relation may be described as a k-ary relation, a k-adic relation, or a k-dimensional relation, respectively.
A more conceptual than nominal variation depends on whether one uses terms like 'predicate', 'relation', and even 'term' to refer to the formal object proper or else to the allied syntactic
items that are used to denote them. Compounded with this variation is still another, frequently associated with philosophical differences over the status in reality accorded formal objects. Among those who speak of numbers, functions, properties, relations, and sets as being real, that is to say, as having objective properties, there are divergences as to whether some things are more real than others, especially whether particulars or properties are equally real or else one derivative of the other. Historically speaking, just about every combination of modalities has been used by one school of thought or another, but it suffices here merely to indicate how the options are generated.
Many relations of the greatest interest in mathematics are triadic relations, but this fact is somewhat disguised by the circumstance that many of them are referred to as binary operation
s, and because the most familiar of these have very specific properties that are dictated by their axioms. This makes it practical to study these operations for quite some time by focusing on their dyadic aspects before being forced to consider their proper characters as triadic relations.
A relation, as conceived in the combinatorial theory of relations, is a mathematical object that in general can have a very complex type, the complexity of which is best approached in several stages, as indicated next.
In order to approach the combinatorial definition of a relation, it helps to introduce a few preliminary notions that can serve as stepping stones to the general idea.
A relation in mathematics is defined as an object that has its existence as such within a definite context or setting. It is literally the case that to change this setting is to change the relation that is being defined. The particular type of context that is needed here is formalized as a collection of elements from which are chosen the elements of the relation in question. This larger collection of elementary relations or tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s is constructed by means of the set-theoretic product commonly known as the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
.
Preliminaries
A relation L is defined by specifying two mathematical objects as its constituent parts:- The first part is called the figure of L, notated as figure(L) or F(L).
- The second part is called the ground of L, notated as ground(L) or G(L).
In the special case of a finitary relation, for concreteness a k-place relation, the concepts of figure and ground are defined as follows:
- The ground of L is a sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of k nonempty sets, X1, …, Xk, called the domains of the relation L.
- The figure of L is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
taken over the domains of L, that is, F(L) ⊆ G(L) = X1 × … × Xk.
Strictly speaking, then, the relation L consists of a couple of things, L = (F(L), G(L)), but it is customary in loose speech to use the single name L in a systematically equivocal fashion, taking it to denote either the couple L = (F(L), G(L)) or the figure F(L). There is usually no confusion about this so long as the ground of the relation can be gathered from context.
Definition
The formal definition of a finitary relation, specifically, a k-ary relation can now be stated.- Definition. A k-ary relation L over the nonempty sets X1, …, Xk is a (1+k)-tuple L = (F(L), X1, …, Xk) where F(L) is a subset of the cartesian product X1 × … × Xk. If all of the Xj for j = 1 to k are the same set X, then L is more simply called a k-ary relation over X. The set F(L) is called the figure of L and, providing that the sequence of sets X1, …, Xk is fixed throughout a given discussion or determinate in context, one may regard the relation L as being determined by its figure F(L).
The formal definition simply repeats more concisely what was said above, merely unwrapping the conceptual packaging of the relation's ground to define the relation in 1 + k parts, as L = (F(X), X1, …, Xk), rather than just the two, as L = (F(L), G(L)).
A k-ary predicate is a boolean-valued function
Boolean-valued function
A boolean-valued function, in some usages is a predicate or a proposition, is a function of the type f : X → B, where X is an arbitrary set and where B is a boolean domain....
on k variables.
Local incidence properties
A local incidence property (LIP) of a relation L is a property that depends in turn on the properties of special subsets of L that are known as its local flags. The local flags of a relation are defined in the following way:Let L be a k-place relation L ⊆ X1 × … × Xk.
Select a relational domain Xj and one of its elements x. Then Lx.j is a subset of L that is referred to as the flag of L with x at j, or the x.j-flag of L, an object which has the following definition:
- Lx.j = { (x1, …, xj, …, xk) ∈ L : xj = x }.
Any property C of the local flag Lx.j ⊆ L is said to be a local incidence property of L with respect to the locus x at j.
A k-adic relation L ⊆ X1 × … × Xk is said to be C-regular at j if and only if every flag of L with x at j has the property C, where x is taken to vary over the theme of the fixed domain Xj.
Expressed in symbols, L is C-regular at j if and only if C(Lx.j) is true for all x in Xj.
Numerical incidence properties
A numerical incidence property (NIP) of a relation is a local incidence property that depends on the cardinalities of its local flags.For example, L is said to be c-regular at j if and only if the cardinality of the local flag Lx.j is c for all x in Xj, or, to write it in symbols, if and only if |Lx.j| = c for all x in Xj.
In a similar fashion, one can define the NIPs (< c)-regular at j, (> c)-regular at j, and so on. For ease of reference, a few of these definitions are recorded here:
 |
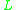is | c-regular | at j | if and only if | = | c | for all x in Xj. | |
 |
is | (< c)-regular | at j | if and only if | < | c | for all x in Xj. | |
 |
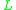is | (> c)-regular | at j | if and only if | > | c | for all x in Xj. |
The definition of a local flag can be broadened from a point x in Xj to a subset M of Xj, arriving at the definition of a regional flag in the following way:
Suppose that L ⊆ X1 × … × Xk, and choose a subset M ⊆ Xj. Then LM.j is a subset of L that is said to be the flag of L with M at j, or the M.j-flag of L, an object which has the following definition:
| LM.j | = | { (x1, …, xj, …, xk) ∈ L : xj ∈ M }. |
Returning to 2-adic relations, it is useful to describe some familiar classes of objects in terms of their local and their numerical incidence properties. Let L ⊆ S × T be an arbitrary 2-adic relation. The following properties of L can be defined:
 |
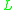is | total | at S | if and only if |  |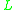
is | (≥1)-regular | at S. |
 |
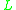is | total | at T | if and only if |  |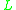
is | (≥1)-regular | at T. |
 |
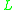is | tubular | at S | if and only if |  |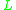
is | (≤1)-regular | at S. |
 |
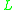is | tubular | at T | if and only if |  |
is | (≤1)-regular | at T. |
If L ⊆ S × T is tubular at S, then L is called a partial function or a prefunction from S to T, sometimes indicated by giving L an alternate name, say, "p", and writing L = p : S
T.Just by way of formalizing the definition:
| L | = | p : S  T |
if and only if | L | is | tubular | at S. |
If L is a prefunction p : S
T that happens to be total at S, then L is called a function from S to T, indicated by writing L = f : S → T. To say that a relation L ⊆ S × T is totally tubular at S is to say that it is 1-regular at S. Thus, we may formalize the following definition:| L | = | f : S → T | if and only if | L | is | 1-regular | at S. |
In the case of a function f : S → T, one has the following additional definitions:
| f | is | surjective | if and only if | f | is | total | at T. |
| f | is | injective | if and only if | f | is | tubular | at T. |
| f | is | bijective | if and only if | f | is | 1-regular | at T. |
Variations
Because the concept of a relation has been developed quite literally from the beginnings of logic and mathematics, and because it has incorporated contributions from a diversity of thinkers from many different times and intellectual climates, there is a wide variety of terminology that the reader may run across in connection with the subject.One dimension of variation is reflected in the names that are given to k-place relations, with some writers using medadic, monadic, dyadic, triadic, k-adic where other writers use nullary, unary, binary, ternary, k-ary.
One finds a relation on a finite number of domains described as either a finitary relation or a polyadic relation. If the number of domains is finite, say equal to k, then the parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
k may be referred to as the arity
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
, the adicity, or the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of the relation. In these cases, the relation may be described as a k-ary relation, a k-adic relation, or a k-dimensional relation, respectively.
A more conceptual than nominal variation depends on whether one uses terms like 'predicate', 'relation', and even 'term' to refer to the formal object proper or else to the allied syntactic
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
items that are used to denote them. Compounded with this variation is still another, frequently associated with philosophical differences over the status in reality accorded formal objects. Among those who speak of numbers, functions, properties, relations, and sets as being real, that is to say, as having objective properties, there are divergences as to whether some things are more real than others, especially whether particulars or properties are equally real or else one derivative of the other. Historically speaking, just about every combination of modalities has been used by one school of thought or another, but it suffices here merely to indicate how the options are generated.
Examples
- See the articles on relationsRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
, relation composition, relation reduction, sign relationSign relationA sign relation is the basic construct in the theory of signs, also known as semeiotic or semiotics, as developed by Charles Sanders Peirce.-Anthesis:...
s, and triadic relationTriadic relationIn mathematics, a ternary relation or triadic relation is a finitary relation in which the number of places in the relation is three. Ternary relations may also be referred to as 3-adic, 3-ary, 3-dimensional, or 3-place....
s for concrete examples of relations.
Many relations of the greatest interest in mathematics are triadic relations, but this fact is somewhat disguised by the circumstance that many of them are referred to as binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s, and because the most familiar of these have very specific properties that are dictated by their axioms. This makes it practical to study these operations for quite some time by focusing on their dyadic aspects before being forced to consider their proper characters as triadic relations.
See also
- Binary operator
- Binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
- FunctionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
- Function compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
- Logic of relatives
- RelationRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
- Relation algebraRelation algebraIn mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
- Relation composition
- Relation constructionRelation constructionIn logic and mathematics, relation construction and relational constructibility have to do with the ways that one relation is determined by an indexed family or a sequence of other relations, called the relation dataset. The relation in the focus of consideration is called the faciendum...
- Relation reduction
- Relational algebraRelational algebraRelational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
- Inverse relationInverse relationIn mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
- Relational databaseRelational databaseA relational database is a database that conforms to relational model theory. The software used in a relational database is called a relational database management system . Colloquial use of the term "relational database" may refer to the RDBMS software, or the relational database itself...
- Relational modelRelational modelThe relational model for database management is a database model based on first-order predicate logic, first formulated and proposed in 1969 by Edgar F...
- Relative termRelative termA relative term is a term that makes two or more distinct references to objects . A relative term is typically expressed in ordinary language by means of a phrase with explicit or implicit blanks...
- RhemeRhemeRheme may refer to:* Rheme in Peirce's semiotics, a sign that represents its object in respect of quality* Topic–comment, a concept in linguistics...
- Triadic relationTriadic relationIn mathematics, a ternary relation or triadic relation is a finitary relation in which the number of places in the relation is three. Ternary relations may also be referred to as 3-adic, 3-ary, 3-dimensional, or 3-place....