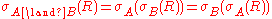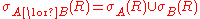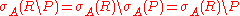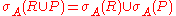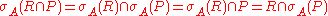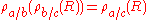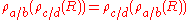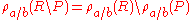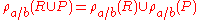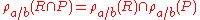Relational algebra
Encyclopedia
Relational algebra, an offshoot of first-order logic
(and of algebra of sets
), deals with a set of finitary relations (see also relation (database)
) that is closed
under certain operators. These operators operate on one or more relations to yield a relation. Relational algebra is a part of computer science
.
's relational model of data
in 1970. Codd proposed such an algebra as a basis for database query languages. (See section Implementations.)
Relational algebra is essentially equivalent in expressive power to relational calculus
(and thus first-order logic
); this result is known as Codd's theorem
. You must be careful to avoid a mismatch, that may arise between the two languages since negation, applied to a formula of the calculus, constructs a formula that may be true on an infinite set of possible tuples, while the difference operator of relational algebra always returns a finite result. To overcome these difficulties, Codd restricted the operands of relational algebra to finite relation
s only and also proposed restricted support for negation (NOT) and disjunction (OR). Analogous restrictions are found in many other logic-based computer languages. Codd defined the term relational completeness to refer to a language that is complete with respect to first-order predicate calculus apart from the restrictions he proposed. In practice the restrictions have no adverse effect on the applicability of his relational algebra for database purposes.
Five primitive operators of Codd's algebra are the selection, the projection, the Cartesian product
(also called the cross product or cross join), the set union, the set difference. Another operator, rename was not noted by Codd, but the need for it is shown by the inventors of ISBL
. These six operators are fundamental in the sense that if you omit any one of them, you will lose expressive power. Many other operators have been defined in terms of these six. Among the most important are set intersection, division, and the natural join. In fact ISBL made a compelling case for replacing the Cartesian product with the natural join, of which the Cartesian product is a degenerate case.
Altogether, the operators of relational algebra have identical expressive power to that of domain relational calculus
or tuple relational calculus
. However, for the reasons given in section Introduction, relational algebra is less expressive than first-order predicate calculus without function symbols. Relational algebra corresponds to a subset of first-order logic
, namely Horn clause
s without recursion and negation.
, there are additional constraints that are present in their relational algebra
counterparts: For set union and set difference, the two relation
s involved must be union-compatible—that is, the two relations must have the same set of attributes. Because set intersection can be defined in terms of set difference, the two relations involved in set intersection must also be union-compatible.
The Cartesian product is defined differently from the one in set theory in the sense that tuples are considered to be 'shallow' for the purposes of the operation. That is, the Cartesian product of an n-tuple by an m-tuple has the 2-tuple "flattened" into an (n + m)-tuple. In set theory, the Cartesian product is a set of 2-tuples. More formally, R × S is defined as follows:
Like the Cartesian product, the cardinality of the result is the product of the cardinalities of its factors, i.e., |R × S| = |R| × |S|. In addition, for the Cartesian product to be defined, the two relations involved must have disjoint headers—that is, they must not have a common attribute name.
written as
where 
is a set of attribute names. The result of such projection is defined as the set that is obtained when all tuple
s in R are restricted to the set
.
This specifies the specific subset of columns (attributes of each tuple) to be retrieved. To obtain the names and phone numbers from an address book, the projection might be written
. The result of that projection would be a relation which contains only the contactName and contactPhoneNumber attributes for each unique entry in addressBook.
written as
where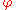 
is a propositional formula
that consists of atom
s as allowed in the normal selection and the logical operators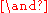
(and
),
(or
) and
(negation
). This selection selects all those tuple
s in R for which
holds.
To obtain a listing of all friends or business associates in an address book, the selection might be written as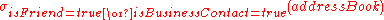
. The result would be a relation containing every attribute of every unique record where isFriend is true or where isBusinessContact is true.
written as
where the result is identical to R except that the b attribute in all tuples is renamed to an a attribute. This is simply used to rename the attribute of a relation
or the relation itself.
To rename the 'isFriend' attribute to 'isBusinessContact' in a relation,
might be used.
) is a binary operator
that is written as (R
S) where R and S are relation
s. The result of the natural join is the set of all combinations of tuples in R and S that are equal on their common attribute names. For an example consider the tables Employee and Dept and their natural join:
|+ Dept
|-
! DeptName !! Manager
|-
| Finance >
| Sales
| Production Charles
|+ Employee 
Dept
|-
! Name !! EmpId !! DeptName !! Manager
|-
| Harry > 3415
Finance
| Sally 2241
Sales
| George 3401
Finance
| Harriet 2202
Sales
Harriet
This can also be used to define composition of relations
. In category theory
, the join is precisely the fiber product.
The natural join is arguably one of the most important operators since it is the relational counterpart of logical AND. Note carefully that if the same variable appears in each of two predicates that are connected by AND, then that variable stands for the same thing and both appearances must always be substituted by the same value. In particular, natural join allows the combination of relations that are associated by a foreign key
. For example, in the above example a foreign key probably holds from Employee.DeptName to Dept.DeptName and then the natural join of Employee and Dept combines all employees with their departments. Note that this works because the foreign key holds between attributes with the same name. If this is not the case such as in the foreign key from Dept.manager to Employee.Name then we have to rename these columns before we take the natural join. Such a join is sometimes also referred to as an equijoin (see θ-join).
More formally the semantics of the natural join is defined as follows:
where Fun is a predicate that is true for a relation
r if and only if
r is a function. It is usually required that R and S must have at least one common attribute, but if this constraint is omitted, and R and S have no common attributes, then the natural join becomes exactly the Cartesian product.
The natural join can be simulated with Codd's primitives as follows. Assume that c1,...,cm are the attribute names common to R and S, r1,...,rn are the
attribute names unique to R and s1,...,sk are the
attribute unique to S. Furthermore assume that the attribute names x1,...,xm are neither in R nor in S. In a first step we can now rename the common attribute names in S:
Then we take the Cartesian product and select the tuples that are to be joined:
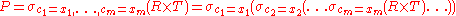
Finally we take a projection to get rid of the renamed attributes:
CarPrice ≥ BoatPrice produces a table with all the possible options. If you are using a condition where the attributes are equal the like Price the condition may be specified as Price=Price
or alternatively (Price) itself.
|+ Boat
|-
! BoatModel !! BoatPrice
|-
| Boat1 >
| Boat2
| Boat3 60'000
|+ 
|-
! CarModel !! CarPrice !! BoatModel !! BoatPrice
|-
| CarA > 20'000
Boat1
| CarB 30'000
Boat1
| CarC 50'000
Boat1
| CarC 50'000
Boat2
40'000
If we want to combine tuples from two relations where the combination condition is not simply the equality of shared attributes then it is convenient to have a more general form of join operator, which is the θ-join (or theta-join). The θ-join is a binary operator that is written as
or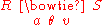 
where a and b are attribute names, θ is a binary relation
in the set {<, ≤, =, >, ≥}, v is a value constant, and R and S are relations. The result of this operation consists of all combinations of tuples in R and S that satisfy the relation θ. The result of the θ-join is defined only if the headers of S and R are disjoint, that is, do not contain a common attribute.
The simulation of this operation in the fundamental operations is therefore as follows:
In case the operator θ is the equality operator (=) then this join is also called an equijoin.
Note, however, that a computer language that supports the natural join and rename operators does not need θ-join as well, as this can be achieved by selection from the result of a natural join (which degenerates to Cartesian product when there are no shared attributes).
S where R and S are relation
s. The result of this semijoin is the set of all tuples in R for which there is a tuple in S that is equal on their common attribute names. For an example consider the tables Employee and Dept and their
semi join:
|+ Dept
|-
! DeptName !! Manager
|-
| Sales >
| Sales
| Production
| Production Mark
|+ Employee 
Dept
|-
! Name !! EmpId !! DeptName
|-
| Sally > 2241
| Harriet 2202
Production
More formally the semantics of the semijoin is defined as
follows:
where Fun(r) is as in the definition of natural join.
The semijoin can be simulated using the natural join as
follows. If a1, ..., an are the
attribute names of R, then
Since we can simulate the natural join with the basic operators it follows that this also holds for the semijoin.
S where R and S are relation
s, is similar to the natural join, but the result of an antijoin is only those tuples in R for which there is no tuple in S that is equal on their common attribute names.
For an example consider the tables Employee and Dept and their
antijoin:
|+ Dept
|-
! DeptName !! Manager
|-
| Sales >
| Production Charles
|+ Employee 
Dept
|-
! Name !! EmpId !! DeptName
|-
| Harry > 3415
| George 3401
Finance
The antijoin is formally defined as follows:
or
where Fun(r) is as in the definition of natural join.
The antijoin can also be defined as the complement
of the semijoin, as follows:
Given this, the antijoin is sometimes called the anti-semijoin, and the antijoin operator is sometimes written as semijoin symbol with a bar above it, instead of
.
DBProject and their division:
|+ DBProject
|-
! Task
|-
| Database1
|-
| Database2>
|+ Completed ÷ DBProject
|-
! Student
|-
| Fred
|-
| Sarah>
If DBProject contains all the tasks of the Database
project, then the result of the division above contains exactly
the students who have completed both of the tasks in the Database project.
More formally the semantics of the division is defined as follows:
where {a1,...,an} is the set of
attribute names unique to R and
t[a1,...,an] is the restriction of
t to this set. It is usually required that the attribute names
in the header of S are a subset of those of R because
otherwise the result of the operation will always be empty.
The simulation of the division with the basic operations is as
follows. We assume that a1,...,an are
the attribute names unique to R and
b1,...,bm are the attribute names of
S. In the first step we project R on its unique attribute
names and construct all combinations with tuples in S:
In the prior example, T would represent a table such that every Student (because Student is the unique key / attribute of the Completed table) is combined with every given Task. So Eugene, for instance, would have two rows, Eugene -> Database1 and Eugene -> Database2 in T.
In the next step we subtract R from this
relation
:
Note that in U we have the possible
combinations that "could have" been in R, but weren't. So if
we now take the projection on the attribute names unique to R
then we have the restrictions of the tuples in R for which not
all combinations with tuples in S were present in R:
So what remains to be done is take the projection of R on its
unique attribute names and subtract those in V:
The operators defined in this section assume the existence of a null value, ω, which we do not define, to be used for the fill values. It should not be assumed that this is the NULL
defined for the database language SQL
, nor should it be assumed that ω is a mark rather than a value, nor should it be assumed that the controversial three-valued logic
is introduced by it.
Three outer join operators are defined: left outer join, right outer join, and full outer join. (The word "outer" is sometimes omitted.)
s. The result of the left outer join is the set of all combinations of tuples in R and S that are equal on their common attribute names, in addition (loosely speaking) to tuples in R that have no matching tuples in S.
For an example consider the tables Employee and Dept and their left outer join:
|+ Dept
|-
! DeptName !! Manager
|-
| Sales >
| Production Charles
|+ Employee ⟕ Dept
|-
! Name !! EmpId !! DeptName !! Manager
|-
| Harry > 3415
Finance
| Sally 2241
Sales
| George 3401
Finance
| Harriet 2202
Sales
| Tim 1123
Executive
ω
In the resulting relation, tuples in S which have no common values in common attribute names with tuples in R take a null value, ω.
Since there are no tuples in Dept with a DeptName of Finance or Executive, ωs occur in the resulting relation where tuples in DeptName have tuples of Finance or Executive.
Let r1, r2, ..., rn be the attributes of the relation R and let {(ω, ..., ω)} be the singleton
relation on the attributes that are unique to the relation S (those that are not attributes of R). Then the left outer join can be described in terms of the natural join (and hence using basic operators) as follows:
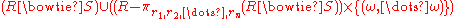
The right outer join of relation
s R and S is written as R ⟖ S. The result of the right outer join is the set of all combinations of tuples in R and S that are equal on their common attribute names, in addition to tuples in S that have no matching tuples in R.
For example consider the tables Employee and Dept and their
right outer join:
|+ Dept
|-
! DeptName !! Manager
|-
| Sales >
| Production Charles
|+ Employee ⟖ Dept
|-
! Name !! EmpId !! DeptName !! Manager
|-
| Sally > 2241
Sales
| Harriet 2202
Sales
| ω ω
Production
Charles
In the resulting relation, tuples in R which have no common values in common attribute names with tuples in S take a null value, ω.
Since there are no tuples in Employee with a DeptName of Production, ωs occur in the Name attribute of the resulting relation where tuples in DeptName had tuples of Production.
Let s1, s2, ..., sn be the attributes of the relation S and let {(ω, ..., ω)} be the singleton
relation on the attributes that are unique to the relation R (those that are not attributes of S). Then, as with the left outer join, the right outer join can be simulated using the natural join as follows:
The full outer join is written as R ⟗ S where R and S are relation
s. The result of the full outer join is the set of all combinations of tuples in R and S that are equal on their common attribute names, in addition to tuples in S that have no matching tuples in R and tuples in R that have no matching tuples in S in their common attribute names.
For an example consider the tables Employee and Dept and their
full outer join:
|+ Dept
|-
! DeptName !! Manager
|-
| Sales >
| Production Charles
|+ Employee ⟗ Dept
|-
! Name !! EmpId !! DeptName !! Manager
|-
| Harry > 3415
Finance
| Sally 2241
Sales
| George 3401
Finance
| Harriet 2202
Sales
| Tim 1123
Executive
| ω ω
Production
Charles
In the resulting relation, tuples in R which have no common values in common attribute names with tuples in S take a null value, ω. Tuples in S which have no common values in common attribute names with tuples in R also take a null value, ω.
The full outer join can be simulated using the left and right outer joins (and hence the natural join and set union) as follows:
s that are included with most databases. These operations are Sum, Count, Average, Maximum and Minimum. In relational algebra the aggregation operation over a schema (A1, A2, ... An) is written as follows:
G1, G2, ..., Gm g f1(A1'), f2(A2'), ..., fk(Ak') (r)
where each Aj', 1 ≤ j ≤ k, is one of the original attributes Ai, 1 ≤ i ≤ n.
The attributes preceding the g are grouping attributes, which function like a "group by" clause in SQL. Then there are an arbitrary number of aggregation functions applied to individual attributes. The operation is applied to an arbitrary relation r. The grouping attributes are optional, and if they are not supplied, the aggregation functions are applied across the entire relation to which the operation is applied.
Let's assume that we have a table named Account with three columns, namely Account_Number, Branch_Name and Balance. We wish to find the maximum balance of each branch. This is accomplished by Branch_NameGMax(Balance)(Account). To find the highest balance of all accounts regardless of branch, we could simply write GMax(Balance)(Account).
s which cannot be expressed by relational algebra. One of them is transitive closure
of a binary relation. Given a domain D, let binary relation R be a subset of DxD. The transitive closure R+ of R is the smallest subset of DxD containing R which satifies the following condition:
x 
y 
z ((x,y) 
R+ 
(y,z) 
R+ 
(x,z) 
R+)
There is no relational algebra expression E(R) taking R as a variable argument which produces R+. This can be proved using the fact that, given a relational expression E for which it is claimed that E(R) = R+, where R is a variable, we can always find an instance r of R (and a corresponding domain d) such that E(r) ≠ r+.
, where
Our primary goal is to transform expression trees into equivalent expression trees, where the average size of the relations yielded by subexpressions in the tree are smaller than they were before the optimization
. Our secondary goal is to try to form common subexpressions within a single query, or if there are more than one queries being evaluated at the same time, in all of those queries. The rationale behind that second goal is that it is enough to compute common subexpressions once, and the results can be used in all queries that contain that subexpression.
Here we present a set of rules, that can be used in such transformations.
s (yielded by subexpressions) will likely shrink.
of simpler conditions is equivalent to a sequence of selections with those same individual conditions, and selection whose condition is a disjunction
is equivalent to a union of selections. These identities can be used to merge selections so that fewer selections need to be evaluated, or to split them so that the component selections may be moved or optimized separately.
s have N and M rows, the result will contain
rows. Therefore it is very important to do our best to decrease the size of both operands before applying the cross product operator.
This can be effectively done, if the cross product is followed by a selection operator, e.g.
(R × P). Considering the definition of join, this is the most likely case. If the cross product is not followed by a selection operator, we can try to push down a selection from higher levels of the expression tree using the other selection rules.
In the above case we break up condition A into conditions B, C and D using the split rules about complex selection conditions, so that A = B
C 
D and B only contains attributes from R, C contains attributes only from P and D contains the part of A that contains attributes from both R and P. Note, that B, C or D are possibly empty. Then the following holds: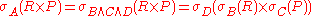
as an operand.
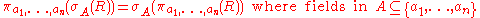
Projection does not distribute over intersection and set difference. Counterexamples are given by:
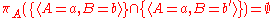
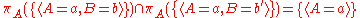
and
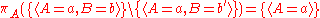
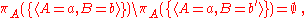
where b is assumed to be distinct from b.
, and this pioneering work has been acclaimed by many authorities as having shown the way to make Codd's idea into a useful language. Business System 12
was a short-lived industry-strength relational DBMS that followed the ISBL example.
In 1998 Chris Date
and Hugh Darwen
proposed a language called Tutorial D intended for use in teaching relational database theory, and its query language also draws on ISBL's ideas. Rel
is an implementation of Tutorial D.
Even the query language of SQL
is loosely based on a relational algebra, though the operands in SQL (table
s) are not exactly relation
s and several useful theorems about the relational algebra do not hold in the SQL counterpart (arguably to the detriment of optimisers and/or users).
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
(and of algebra of sets
Algebra of sets
The algebra of sets develops and describes the basic properties and laws of sets, the set-theoretic operations of union, intersection, and complementation and the relations of set equality and set inclusion...
), deals with a set of finitary relations (see also relation (database)
Relation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
) that is closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under certain operators. These operators operate on one or more relations to yield a relation. Relational algebra is a part of computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.
Introduction
Relational algebra received little attention outside of pure mathematics until the publication of E.F. CoddEdgar F. Codd
Edgar Frank "Ted" Codd was an English computer scientist who, while working for IBM, invented the relational model for database management, the theoretical basis for relational databases...
's relational model of data
Relational model
The relational model for database management is a database model based on first-order predicate logic, first formulated and proposed in 1969 by Edgar F...
in 1970. Codd proposed such an algebra as a basis for database query languages. (See section Implementations.)
Relational algebra is essentially equivalent in expressive power to relational calculus
Relational calculus
Relational calculus consists of two calculi, the tuple relational calculus and the domain relational calculus, that are part of the relational model for databases and provide a declarative way to specify database queries...
(and thus first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
); this result is known as Codd's theorem
Codd's theorem
Codd's theorem states that relational algebra and the domain-independent relational calculus queries, two well-known foundational query languages for the relational model, are precisely equivalent in expressive power. That is, a database query can be formulated in one language if and only if it can...
. You must be careful to avoid a mismatch, that may arise between the two languages since negation, applied to a formula of the calculus, constructs a formula that may be true on an infinite set of possible tuples, while the difference operator of relational algebra always returns a finite result. To overcome these difficulties, Codd restricted the operands of relational algebra to finite relation
Relation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s only and also proposed restricted support for negation (NOT) and disjunction (OR). Analogous restrictions are found in many other logic-based computer languages. Codd defined the term relational completeness to refer to a language that is complete with respect to first-order predicate calculus apart from the restrictions he proposed. In practice the restrictions have no adverse effect on the applicability of his relational algebra for database purposes.
Primitive operations
As in any algebra, some operators are primitive and the others are derived in terms of the primitive ones. It is useful if the choice of primitive operators parallels the usual choice of primitive logical operators. Although it is well known that the usual choice in logic of AND, OR and NOT is somewhat arbitrary, Codd made a similar arbitrary choice for his algebra.Five primitive operators of Codd's algebra are the selection, the projection, the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
(also called the cross product or cross join), the set union, the set difference. Another operator, rename was not noted by Codd, but the need for it is shown by the inventors of ISBL
ISBL
ISBL is the relational algebra notation that was invented for PRTV, one of the earliest database management systems to implement E.F. Codd's relational model of data.-See also:...
. These six operators are fundamental in the sense that if you omit any one of them, you will lose expressive power. Many other operators have been defined in terms of these six. Among the most important are set intersection, division, and the natural join. In fact ISBL made a compelling case for replacing the Cartesian product with the natural join, of which the Cartesian product is a degenerate case.
Altogether, the operators of relational algebra have identical expressive power to that of domain relational calculus
Domain relational calculus
In computer science, domain relational calculus is a calculus that was introduced by Michel Lacroix and Alain Pirotte as a declarative database query language for the relational data model.In DRC, queries have the form:...
or tuple relational calculus
Tuple relational calculus
Tuple calculus is a calculus that was introduced by Edgar F. Codd as part of the relational model, in order to provide a declarative database-query language for this data model...
. However, for the reasons given in section Introduction, relational algebra is less expressive than first-order predicate calculus without function symbols. Relational algebra corresponds to a subset of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, namely Horn clause
Horn clause
In mathematical logic, a Horn clause is a clause with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951...
s without recursion and negation.
Set operators
Although three of the six basic operators are taken from set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, there are additional constraints that are present in their relational algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
counterparts: For set union and set difference, the two relation
Relation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s involved must be union-compatible—that is, the two relations must have the same set of attributes. Because set intersection can be defined in terms of set difference, the two relations involved in set intersection must also be union-compatible.
The Cartesian product is defined differently from the one in set theory in the sense that tuples are considered to be 'shallow' for the purposes of the operation. That is, the Cartesian product of an n-tuple by an m-tuple has the 2-tuple "flattened" into an (n + m)-tuple. In set theory, the Cartesian product is a set of 2-tuples. More formally, R × S is defined as follows:
- R × S = {(r1, r2, ..., rn, s1, s2, ..., sm) | (r1, r2, ..., rn) ∈ R, (s1, s2, ..., sm) ∈ S}
Like the Cartesian product, the cardinality of the result is the product of the cardinalities of its factors, i.e., |R × S| = |R| × |S|. In addition, for the Cartesian product to be defined, the two relations involved must have disjoint headers—that is, they must not have a common attribute name.
Projection
A projection is a unary operationUnary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
written as
where is a set of attribute names. The result of such projection is defined as the set that is obtained when all tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s in R are restricted to the set
.This specifies the specific subset of columns (attributes of each tuple) to be retrieved. To obtain the names and phone numbers from an address book, the projection might be written
. The result of that projection would be a relation which contains only the contactName and contactPhoneNumber attributes for each unique entry in addressBook.Selection (σ)
A generalized selection is a unary operationUnary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
written as
where 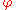is a propositional formulaPropositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
that consists of atom
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
s as allowed in the normal selection and the logical operators
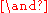(andLogical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
),
(orLogical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
) and
(negationNegation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
). This selection selects all those tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s in R for which
holds.To obtain a listing of all friends or business associates in an address book, the selection might be written as
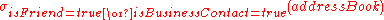. The result would be a relation containing every attribute of every unique record where isFriend is true or where isBusinessContact is true.Rename (ρ)
A rename is a unary operationUnary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
written as
where the result is identical to R except that the b attribute in all tuples is renamed to an a attribute. This is simply used to rename the attribute of a relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
or the relation itself.
To rename the 'isFriend' attribute to 'isBusinessContact' in a relation,
might be used.Natural joins (
) is a binary operatorBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
that is written as (R
S) where R and S are relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s. The result of the natural join is the set of all combinations of tuples in R and S that are equal on their common attribute names. For an example consider the tables Employee and Dept and their natural join:
|
|- ! Name !! EmpId !! DeptName |- | Harry > | 3415 | >- | 2241 | >- | 3401 | >- | 2202 | Sales |
|-
! DeptName !! Manager
|-
| Finance >
| Sales
| Production
Dept|-
! Name !! EmpId !! DeptName !! Manager
|-
| Harry >
| Sally
| George
| Harriet
This can also be used to define composition of relations
Composition of relations
In mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
. In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the join is precisely the fiber product.
The natural join is arguably one of the most important operators since it is the relational counterpart of logical AND. Note carefully that if the same variable appears in each of two predicates that are connected by AND, then that variable stands for the same thing and both appearances must always be substituted by the same value. In particular, natural join allows the combination of relations that are associated by a foreign key
Foreign key
In the context of relational databases, a foreign key is a referential constraint between two tables.A foreign key is a field in a relational table that matches a candidate key of another table...
. For example, in the above example a foreign key probably holds from Employee.DeptName to Dept.DeptName and then the natural join of Employee and Dept combines all employees with their departments. Note that this works because the foreign key holds between attributes with the same name. If this is not the case such as in the foreign key from Dept.manager to Employee.Name then we have to rename these columns before we take the natural join. Such a join is sometimes also referred to as an equijoin (see θ-join).
More formally the semantics of the natural join is defined as follows:
where Fun is a predicate that is true for a relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
r if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
r is a function. It is usually required that R and S must have at least one common attribute, but if this constraint is omitted, and R and S have no common attributes, then the natural join becomes exactly the Cartesian product.
The natural join can be simulated with Codd's primitives as follows. Assume that c1,...,cm are the attribute names common to R and S, r1,...,rn are the
attribute names unique to R and s1,...,sk are the
attribute unique to S. Furthermore assume that the attribute names x1,...,xm are neither in R nor in S. In a first step we can now rename the common attribute names in S:
Then we take the Cartesian product and select the tuples that are to be joined:
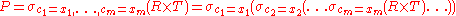
Finally we take a projection to get rid of the renamed attributes:
θ-join and equijoin
Consider tables Car and Boat which list models of cars and boats and their respective prices. Suppose a customer wants to buy a car and a boat, but she does not want to spend more money for the boat than for the car. The θ-join on the relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
CarPrice ≥ BoatPrice produces a table with all the possible options. If you are using a condition where the attributes are equal the like Price the condition may be specified as Price=Price
or alternatively (Price) itself.
|
|- ! CarModel !! CarPrice |- | CarA > | >- | >- | 50'000 |
|-
! BoatModel !! BoatPrice
|-
| Boat1 >
| Boat2
| Boat3
|-
! CarModel !! CarPrice !! BoatModel !! BoatPrice
|-
| CarA >
| CarB
| CarC
| CarC
If we want to combine tuples from two relations where the combination condition is not simply the equality of shared attributes then it is convenient to have a more general form of join operator, which is the θ-join (or theta-join). The θ-join is a binary operator that is written as
or 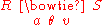where a and b are attribute names, θ is a binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
in the set {<, ≤, =, >, ≥}, v is a value constant, and R and S are relations. The result of this operation consists of all combinations of tuples in R and S that satisfy the relation θ. The result of the θ-join is defined only if the headers of S and R are disjoint, that is, do not contain a common attribute.
The simulation of this operation in the fundamental operations is therefore as follows:
- R
φ S = σφ(R × S)
In case the operator θ is the equality operator (=) then this join is also called an equijoin.
Note, however, that a computer language that supports the natural join and rename operators does not need θ-join as well, as this can be achieved by selection from the result of a natural join (which degenerates to Cartesian product when there are no shared attributes).
(⋉)(⋊)
The left semijoin is joining similar to the natural join and written as R S where R and S are relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s. The result of this semijoin is the set of all tuples in R for which there is a tuple in S that is equal on their common attribute names. For an example consider the tables Employee and Dept and their
semi join:
|
|- ! Name !! EmpId !! DeptName |- | Harry > | 3415 | >- | 2241 | >- | 3401 | >- | 2202 | Production |
|-
! DeptName !! Manager
|-
| Sales >
| Sales
| Production
| Production
Dept|-
! Name !! EmpId !! DeptName
|-
| Sally >
| Harriet
More formally the semantics of the semijoin is defined as
follows:
- R
S = { t : t 
R, s 
S, Fun (t 
s) }
where Fun(r) is as in the definition of natural join.
The semijoin can be simulated using the natural join as
follows. If a1, ..., an are the
attribute names of R, then
- R
S = 
a1,..,an(R 
S).
Since we can simulate the natural join with the basic operators it follows that this also holds for the semijoin.
(▷)
The antijoin, written as R S where R and S are relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s, is similar to the natural join, but the result of an antijoin is only those tuples in R for which there is no tuple in S that is equal on their common attribute names.
For an example consider the tables Employee and Dept and their
antijoin:
|
|- ! Name !! EmpId !! DeptName |- | Harry > | 3415 | >- | 2241 | >- | 3401 | >- | 2202 | Production |
|-
! DeptName !! Manager
|-
| Sales >
| Production
Dept|-
! Name !! EmpId !! DeptName
|-
| Harry >
| George
The antijoin is formally defined as follows:
- R
S = { t : t 
R 
s 
S : Fun (t 
s) }
or
- R
S = { t : t 
R, there is no tuple s of S that satisfies Fun (t 
s) }
where Fun(r) is as in the definition of natural join.
The antijoin can also be defined as the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the semijoin, as follows:
- R
S = R − R 
S
Given this, the antijoin is sometimes called the anti-semijoin, and the antijoin operator is sometimes written as semijoin symbol with a bar above it, instead of
.(÷)
The division is a binary operation that is written as R ÷ S. The result consists of the restrictions of tuples in R to the attribute names unique to R, i.e., in the header of R but not in the header of S, for which it holds that all their combinations with tuples in S are present in R. For an example see the tables Completed,DBProject and their division:
|
|- ! Student !! Task |- | Fred > | >- | >- | >- | >- | >- | >- | Database2 |
|-
! Task
|-
| Database1
|-
| Database2>
|-
! Student
|-
| Fred
|-
| Sarah>
If DBProject contains all the tasks of the Database
project, then the result of the division above contains exactly
the students who have completed both of the tasks in the Database project.
More formally the semantics of the division is defined as follows:
- R ÷ S = { t[a1,...,an] : t
R 
s 
S ( (t[a1,...,an] 
s) 
R) }
where {a1,...,an} is the set of
attribute names unique to R and
t[a1,...,an] is the restriction of
t to this set. It is usually required that the attribute names
in the header of S are a subset of those of R because
otherwise the result of the operation will always be empty.
The simulation of the division with the basic operations is as
follows. We assume that a1,...,an are
the attribute names unique to R and
b1,...,bm are the attribute names of
S. In the first step we project R on its unique attribute
names and construct all combinations with tuples in S:
- T := πa1,...,an(R) × S
In the prior example, T would represent a table such that every Student (because Student is the unique key / attribute of the Completed table) is combined with every given Task. So Eugene, for instance, would have two rows, Eugene -> Database1 and Eugene -> Database2 in T.
In the next step we subtract R from this
relation
Relation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
:
- U := T − R
Note that in U we have the possible
combinations that "could have" been in R, but weren't. So if
we now take the projection on the attribute names unique to R
then we have the restrictions of the tuples in R for which not
all combinations with tuples in S were present in R:
- V := πa1,...,an(U)
So what remains to be done is take the projection of R on its
unique attribute names and subtract those in V:
- W := πa1,...,an(R) − V
Outer joins
Whereas the result of a join (or inner join) consists of tuples formed by combining matching tuples in the two operands, an outer join contains those tuples and additionally some tuples formed by extending an unmatched tuple in one of the operands by "fill" values for each of the attributes of the other operand.The operators defined in this section assume the existence of a null value, ω, which we do not define, to be used for the fill values. It should not be assumed that this is the NULL
Null (SQL)
Null is a special marker used in Structured Query Language to indicate that a data value does not exist in the database. Introduced by the creator of the relational database model, E. F. Codd, SQL Null serves to fulfill the requirement that all true relational database management systems support...
defined for the database language SQL
SQL
SQL is a programming language designed for managing data in relational database management systems ....
, nor should it be assumed that ω is a mark rather than a value, nor should it be assumed that the controversial three-valued logic
Ternary logic
In logic, a three-valued logic is any of several many-valued logic systems in which there are three truth values indicating true, false and some indeterminate third value...
is introduced by it.
Three outer join operators are defined: left outer join, right outer join, and full outer join. (The word "outer" is sometimes omitted.)
(⟕)
The left outer join is written as R ⟕ S where R and S are relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s. The result of the left outer join is the set of all combinations of tuples in R and S that are equal on their common attribute names, in addition (loosely speaking) to tuples in R that have no matching tuples in S.
For an example consider the tables Employee and Dept and their left outer join:
|
|- ! Name !! EmpId !! DeptName |- | Harry > | 3415 | >- | 2241 | >- | 3401 | >- | 2202 | >- | 1123 | Executive |
|-
! DeptName !! Manager
|-
| Sales >
| Production
|-
! Name !! EmpId !! DeptName !! Manager
|-
| Harry >
| Sally
| George
| Harriet
| Tim
In the resulting relation, tuples in S which have no common values in common attribute names with tuples in R take a null value, ω.
Since there are no tuples in Dept with a DeptName of Finance or Executive, ωs occur in the resulting relation where tuples in DeptName have tuples of Finance or Executive.
Let r1, r2, ..., rn be the attributes of the relation R and let {(ω, ..., ω)} be the singleton
relation on the attributes that are unique to the relation S (those that are not attributes of R). Then the left outer join can be described in terms of the natural join (and hence using basic operators) as follows:
(⟖)
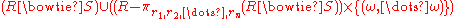
The right outer join behaves almost identically to the left outer join, but the roles of the tables are switched.The right outer join of relation
Relation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s R and S is written as R ⟖ S. The result of the right outer join is the set of all combinations of tuples in R and S that are equal on their common attribute names, in addition to tuples in S that have no matching tuples in R.
For example consider the tables Employee and Dept and their
right outer join:
|
|- ! Name !! EmpId !! DeptName |- | Harry > | 3415 | >- | 2241 | >- | 3401 | >- | 2202 | >- | 1123 | Executive |
|-
! DeptName !! Manager
|-
| Sales >
| Production
|-
! Name !! EmpId !! DeptName !! Manager
|-
| Sally >
| Harriet
| ω
In the resulting relation, tuples in R which have no common values in common attribute names with tuples in S take a null value, ω.
Since there are no tuples in Employee with a DeptName of Production, ωs occur in the Name attribute of the resulting relation where tuples in DeptName had tuples of Production.
Let s1, s2, ..., sn be the attributes of the relation S and let {(ω, ..., ω)} be the singleton
relation on the attributes that are unique to the relation R (those that are not attributes of S). Then, as with the left outer join, the right outer join can be simulated using the natural join as follows:
(⟗)
The outer join or full outer join in effect combines the results of the left and right outer joins.The full outer join is written as R ⟗ S where R and S are relation
Relation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s. The result of the full outer join is the set of all combinations of tuples in R and S that are equal on their common attribute names, in addition to tuples in S that have no matching tuples in R and tuples in R that have no matching tuples in S in their common attribute names.
For an example consider the tables Employee and Dept and their
full outer join:
|
|- ! Name !! EmpId !! DeptName |- | Harry > | 3415 | >- | 2241 | >- | 3401 | >- | 2202 | >- | 1123 | Executive |
|-
! DeptName !! Manager
|-
| Sales >
| Production
|-
! Name !! EmpId !! DeptName !! Manager
|-
| Harry >
| Sally
| George
| Harriet
| Tim
| ω
In the resulting relation, tuples in R which have no common values in common attribute names with tuples in S take a null value, ω. Tuples in S which have no common values in common attribute names with tuples in R also take a null value, ω.
The full outer join can be simulated using the left and right outer joins (and hence the natural join and set union) as follows:
- R ⟗ S = (R ⟕ S)
(R ⟖ S)
Aggregation
There are five aggregate functionAggregate function
In computer science, an aggregate function is a function where the values of multiple rows are grouped together as input on certain criteria to form a single value of more significant meaning or measurement such as a set, a bag or a list....
s that are included with most databases. These operations are Sum, Count, Average, Maximum and Minimum. In relational algebra the aggregation operation over a schema (A1, A2, ... An) is written as follows:
G1, G2, ..., Gm g f1(A1'), f2(A2'), ..., fk(Ak') (r)
where each Aj', 1 ≤ j ≤ k, is one of the original attributes Ai, 1 ≤ i ≤ n.
The attributes preceding the g are grouping attributes, which function like a "group by" clause in SQL. Then there are an arbitrary number of aggregation functions applied to individual attributes. The operation is applied to an arbitrary relation r. The grouping attributes are optional, and if they are not supplied, the aggregation functions are applied across the entire relation to which the operation is applied.
Let's assume that we have a table named Account with three columns, namely Account_Number, Branch_Name and Balance. We wish to find the maximum balance of each branch. This is accomplished by Branch_NameGMax(Balance)(Account). To find the highest balance of all accounts regardless of branch, we could simply write GMax(Balance)(Account).
The extend operation
The extend operation is used for computed attributes. For example, if you have an attribute that contains the price of some item and another attribute that contains the quantity of that item, you can form a computed attribute: EXTEND (price * quantity) AS Total_Price.Limitation of relational algebra
Although relational algebra seems powerful enough for most practical purposes, there are some simple and natural operators on relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s which cannot be expressed by relational algebra. One of them is transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of a binary relation. Given a domain D, let binary relation R be a subset of DxD. The transitive closure R+ of R is the smallest subset of DxD containing R which satifies the following condition:
x y z ((x,y) R+ (y,z) R+ (x,z) R+)There is no relational algebra expression E(R) taking R as a variable argument which produces R+. This can be proved using the fact that, given a relational expression E for which it is claimed that E(R) = R+, where R is a variable, we can always find an instance r of R (and a corresponding domain d) such that E(r) ≠ r+.
Use of algebraic properties for query optimization
Queries can be represented as a treeTree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
, where
- the internal nodes are operators,
- leaves are relationRelation (database)In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s, - subtrees are subexpressions.
Our primary goal is to transform expression trees into equivalent expression trees, where the average size of the relations yielded by subexpressions in the tree are smaller than they were before the optimization
Query optimization
Query optimization is a function of many relational database management systems in which multiple query plans for satisfying a query are examined and a good query plan is identified. This may or not be the absolute best strategy because there are many ways of doing plans. There is a trade-off...
. Our secondary goal is to try to form common subexpressions within a single query, or if there are more than one queries being evaluated at the same time, in all of those queries. The rationale behind that second goal is that it is enough to compute common subexpressions once, and the results can be used in all queries that contain that subexpression.
Here we present a set of rules, that can be used in such transformations.
Selection
Rules about selection operators play the most important role in query optimization. Selection is an operator that very effectively decreases the number of rows in its operand, so if we manage to move the selections in an expression tree towards the leaves, the internal relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s (yielded by subexpressions) will likely shrink.
Basic selection properties
Selection is idempotent (multiple applications of the same selection have no additional effect beyond the first one), and commutative (the order selections are applied in has no effect on the eventual result).
Breaking up selections with complex conditions
A selection whose condition is a conjunctionLogical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
of simpler conditions is equivalent to a sequence of selections with those same individual conditions, and selection whose condition is a disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
is equivalent to a union of selections. These identities can be used to merge selections so that fewer selections need to be evaluated, or to split them so that the component selections may be moved or optimized separately.
Selection and cross product
Cross product is the costliest operator to evaluate. If the input relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s have N and M rows, the result will contain
rows. Therefore it is very important to do our best to decrease the size of both operands before applying the cross product operator.This can be effectively done, if the cross product is followed by a selection operator, e.g.
(R × P). Considering the definition of join, this is the most likely case. If the cross product is not followed by a selection operator, we can try to push down a selection from higher levels of the expression tree using the other selection rules.In the above case we break up condition A into conditions B, C and D using the split rules about complex selection conditions, so that A = B
C D and B only contains attributes from R, C contains attributes only from P and D contains the part of A that contains attributes from both R and P. Note, that B, C or D are possibly empty. Then the following holds: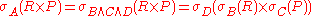Selection and set operators
Selection is distributive over the setminus, intersection, and union operators. The following three rules are used to push selection below set operations in the expression tree. Note, that in the setminus and the intersection operators it is possible to apply the selection operator to only one of the operands after the transformation. This can make sense in cases, where one of the operands is small, and the overhead of evaluating the selection operator outweighs the benefits of using a smaller relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
as an operand.
Selection and projection
Selection is associative with projection if and only if the fields referenced in the selection condition are a subset of the fields in the projection. Performing selection before projection may be useful if the operand is a cross product or join. In other cases, if the selection condition is relatively expensive to compute, moving selection outside the projection may reduce the number of tuples which must be tested (since projection may produce fewer tuples due to the elimination of duplicates resulting from elided fields).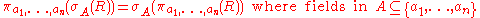Basic projection properties
Projection is idempotent, so that a series of (valid) projections is equivalent to the outermost projection.Projection and set operators
Projection is distributive over set union.Projection does not distribute over intersection and set difference. Counterexamples are given by:
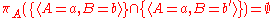
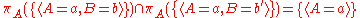
and
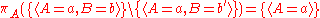
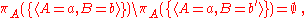
where b is assumed to be distinct from b.
Basic rename properties
Successive renames of a variable can be collapsed into a single rename. Rename operations which have no variables in common can be arbitrarily reordered with respect to one another, which can be exploited to make successive renames adjacent so that they can be collapsed.
Rename and set operators
Rename is distributive over set difference, union, and intersection.
Implementations
The first query language to be based on Codd's algebra was ISBLISBL
ISBL is the relational algebra notation that was invented for PRTV, one of the earliest database management systems to implement E.F. Codd's relational model of data.-See also:...
, and this pioneering work has been acclaimed by many authorities as having shown the way to make Codd's idea into a useful language. Business System 12
Business System 12
Business System 12, or simply BS12, was one of the first fully relational database management systems, designed and implemented by IBM's Bureau Service subsidiary at the company's international development centre in Uithoorn, Netherlands. Programming started in 1978 and the first version was...
was a short-lived industry-strength relational DBMS that followed the ISBL example.
In 1998 Chris Date
Christopher J. Date
Chris Date is an independent author, lecturer, researcher, and consultant, specializing in relational database theory.-Biography:Chris Date attended High Wycombe Royal Grammar School from 1951 to 1958 and received his BA in Mathematics from Cambridge University in 1962. He entered the computer...
and Hugh Darwen
Hugh Darwen
Hugh Darwen is a computer scientist who was an employee of IBM United Kingdom from 1967 to 2004, and has been involved in the history of the relational model.- Work :...
proposed a language called Tutorial D intended for use in teaching relational database theory, and its query language also draws on ISBL's ideas. Rel
Rel (DBMS)
Rel is an open source true relational database management system that implements a significant portion of Chris Date and Hugh Darwen's Tutorial D query language.Primarily intended for teaching purposes, Rel is written in the Java programming language....
is an implementation of Tutorial D.
Even the query language of SQL
SQL
SQL is a programming language designed for managing data in relational database management systems ....
is loosely based on a relational algebra, though the operands in SQL (table
Table (database)
In relational databases and flat file databases, a table is a set of data elements that is organized using a model of vertical columns and horizontal rows. A table has a specified number of columns, but can have any number of rows...
s) are not exactly relation
Relation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
s and several useful theorems about the relational algebra do not hold in the SQL counterpart (arguably to the detriment of optimisers and/or users).
External links
- RAT. Software Relational Algebra Translator to SQL
- Lecture Notes: Relational Algebra – A quick tutorial to adapt SQL queries into relational algebra
- LEAP – An implementation of the relational algebra
- Relational – A graphic implementation of the relational algebra
- Query Optimization This paper is an introduction into the use of the relational algebra in optimizing queries, and includes numerous citations for more in-depth study.
- bandilab.org – neat graphical illustrations of the relational operators
- Relational Algebra System for Oracle and Microsoft SQL Server