Projection (relational algebra)
Encyclopedia
In relational algebra
, a projection is a unary operation
written as where
where  is a set of attribute names. The result of such projection is defined as the set obtained when the components of the tuple
is a set of attribute names. The result of such projection is defined as the set obtained when the components of the tuple
 are restricted to the set
are restricted to the set  – it discards (or excludes) the other attributes.
– it discards (or excludes) the other attributes.
In practical terms, it can be roughly thought of as picking a sub-set of all available columns. For example, if the attributes are (name, age), then projection of the relation {(Alice, 5), (Bob, 8)} onto attribute list (age) yields {5,8} – we have discarded the names, and only know what ages are present.
(see: projection (set theory)) differs from that of relational algebra
in that, in set theory, one projects onto ordered components, not onto attributes. For instance, projecting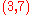 onto the second component yields 7.
onto the second component yields 7.
Projection is relational algebra's counterpart of existential quantification
in predicate logic
. The attributes not included correspond to existentially quantified variables in the predicate whose extension
the operand relation represents. The example below illustrates this point.
Because of the correspondence with existential quantification, some authorities prefer to define projection in terms of the excluded attributes. In a computer language it is of course possible to provide notations for both, and that was done in ISBL
and several languages that have taken their cue from ISBL.
A nearly identical concept occurs in the category of monoid
s, called a string projection, which consists of removing all of the letters in the string
that do not belong to a given alphabet
.
 and its projection on (some say "over") the attributes
and its projection on (some say "over") the attributes 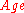 and
and  :
:
Suppose the predicate of Person is "Name is age years old and weighs weight." Then the given projection represents the predicate, "There exists Name such that Name is age years old and weighs weight."
Note that Harry and Peter have the same age and weight, but since the result is a relation, and therefore a set, this combination only appears once in the result.
More formally the semantics of projection are defined as follows:
where is the restriction
is the restriction
of the tuple to the set
to the set  so that
so that
The result of a projection is defined only if
is defined only if  is a subset
is a subset
of the header
of .
.
It is interesting to note that projection over no attributes at all is possible, yielding a relation of degree zero. In this case the cardinality of the result is zero if the operand is empty, otherwise one. The two relations of degree zero are the only ones that cannot be depicted as tables.
Relational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
, a projection is a unary operation
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
written as
 where
where  is a set of attribute names. The result of such projection is defined as the set obtained when the components of the tuple
is a set of attribute names. The result of such projection is defined as the set obtained when the components of the tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
 are restricted to the set
are restricted to the set  – it discards (or excludes) the other attributes.
– it discards (or excludes) the other attributes.In practical terms, it can be roughly thought of as picking a sub-set of all available columns. For example, if the attributes are (name, age), then projection of the relation {(Alice, 5), (Bob, 8)} onto attribute list (age) yields {5,8} – we have discarded the names, and only know what ages are present.
Related concepts
The closely related concept in set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
(see: projection (set theory)) differs from that of relational algebra
Relational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
in that, in set theory, one projects onto ordered components, not onto attributes. For instance, projecting
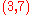 onto the second component yields 7.
onto the second component yields 7.Projection is relational algebra's counterpart of existential quantification
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
in predicate logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. The attributes not included correspond to existentially quantified variables in the predicate whose extension
Extension (predicate logic)
The extension of a predicatea truth-valued functionis the set of tuples of values that, used as arguments, satisfy the predicate. Such a set of tuples is a relation.For example the statement "d2 is the weekday following d1"...
the operand relation represents. The example below illustrates this point.
Because of the correspondence with existential quantification, some authorities prefer to define projection in terms of the excluded attributes. In a computer language it is of course possible to provide notations for both, and that was done in ISBL
ISBL
ISBL is the relational algebra notation that was invented for PRTV, one of the earliest database management systems to implement E.F. Codd's relational model of data.-See also:...
and several languages that have taken their cue from ISBL.
A nearly identical concept occurs in the category of monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s, called a string projection, which consists of removing all of the letters in the string
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
that do not belong to a given alphabet
Alphabet
An alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
.
Example
For an example, consider the relations depicted in the following two tables which are the relation and its projection on (some say "over") the attributes
and its projection on (some say "over") the attributes 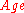 and
and  :
:  |
 |
|---|---|
Suppose the predicate of Person is "Name is age years old and weighs weight." Then the given projection represents the predicate, "There exists Name such that Name is age years old and weighs weight."
Note that Harry and Peter have the same age and weight, but since the result is a relation, and therefore a set, this combination only appears once in the result.
More formally the semantics of projection are defined as follows:
where
 is the restriction
is the restrictionRestriction
Restriction may refer to:* Restriction , an aspect of a mathematical function* Restrictions , an album by Cactus* Restriction enzyme, a type of enzyme that cleaves genetic material...
of the tuple
 to the set
to the set  so that
so thatThe result of a projection
 is defined only if
is defined only if  is a subset
is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the header
Header
Header may refer to: Computers and engineering* Header , supplemental data at the beginning of a data block** E-mail header** HTTP header* Header file, a text file used in computer programming...
of
 .
.It is interesting to note that projection over no attributes at all is possible, yielding a relation of degree zero. In this case the cardinality of the result is zero if the operand is empty, otherwise one. The two relations of degree zero are the only ones that cannot be depicted as tables.