Extension of scalars
Encyclopedia
In abstract algebra
, extension of scalars is a means of producing a module
over a ring
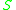from a module over another ring 
, given a homomorphism
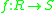between them. Intuitively, the new module admits multiplication by more scalars than the original one, hence the name extension.
, or to have an identity
. Also, modules are assumed to be left modules. The modifications needed in the case of right modules are straightforward.
Let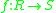
be a homomorphism between two rings, and let 
be a module over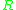 
. Consider the tensor product
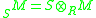, where 
is regarded as a right 
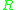-module via 
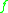. Since 
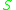is also a left module over itself, and the two actions commute, that is 
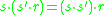for 
, 
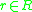(in a more formal language, 
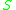is a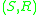 
-bimodule
),
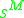inherits a left action of 
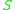. It is given by 
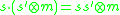for 
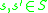and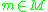 
. This module is said to be obtained from 
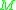through extension of scalars.
Informally, extension of scalars is "the tensor product of a ring and a module"; more formally, it is a special case of a tensor product of a bimodule and a module – the tensor product of an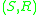
bimodule with an R-module is an S-module.
, which is extension of scalars from the real number
s to the complex number
s. More generally, given any field extension
K < L, one can extend scalars from K to L. In the language of fields, as module over a field is called a vector space
, and thus extension of scalars converts a vector space over K to a vector space over L. This can also be done for division algebra
s, as is done in quaternionification (extension from the reals to the quaternion
s).
More generally, given an homomorphism from a field or commutative ring R to a ring S, the ring S can be thought of as an associative algebra
over R, and thus when one extends scalars on an R-module, the resulting module can be thought of alternatively as an S-module, or as an R-module with an algebra representation of S (as an R-algebra). For example, the result of complexifying a real vector space (R = R, S = C) can be interpreted either as a complex vector space (S-module) or as a real vector space with a linear complex structure
(algebra representation of S as an R-module).
. Just as one can extend scalars on vector spaces, one can also extend scalars on group algebra
s and also on modules over group algebras, i.e., group representation
s. Particularly useful is relating how irreducible representations change under extension of scalars – for example, the representation of the cyclic group of order 4, given by rotation of the plane by 90°, is an irreducible 2-dimensional real representation, but on extension of scalars to the complex numbers, it split into 2 complex representations of dimension 1. This corresponds to the fact that the characteristic polynomial
of this operator,
is irreducible of degree 2 over the reals, but factors into 2 factors of degree 1 over the complex numbers – it has no real eigenvalues, but 2 complex eigenvalues.
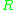-modules to 
-modules. It sends 
to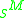 
, as above, and an 
-homomorphism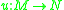 
to the 
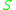-homomorphism 
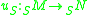defined by 
.
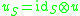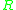-module 
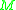and an 
-module 
. Given a homomorphism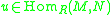 
, where 
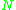is viewed as an 
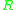-module via restriction of scalars
, define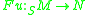
to be the composition
,
where the last map is
. This 
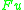is an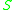 
-homomorphism, and hence 
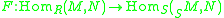is well-defined, and is a homomorphism (of abelian groups
).
In case both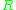
and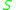 
have an identity, there is an inverse homomorphism 
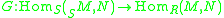, which is defined as follows. Let 
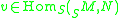. Then 
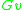is the composition
,
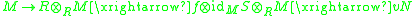where the first map is the canonical
isomorphism
.
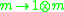This construction shows that the groups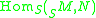
and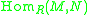 
are isomorphic. Actually, this isomorphism depends only on the homomorphism 
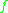, and so is functorial. In the language of category theory
, the extension of scalars functor is left adjoint to the restriction of scalars functor.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, extension of scalars is a means of producing a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
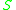from a module over another ring , given a homomorphismRing homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
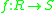between them. Intuitively, the new module admits multiplication by more scalars than the original one, hence the name extension.Definition
In this definition the rings are assumed to be associative, but not necessarily commutativeCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, or to have an identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. Also, modules are assumed to be left modules. The modifications needed in the case of right modules are straightforward.
Let
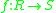be a homomorphism between two rings, and let be a module over 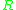. Consider the tensor productTensor product of modules
In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps to be carried out in terms of linear maps...
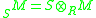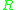, where is regarded as a right -module via 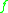. Since 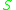is also a left module over itself, and the two actions commute, that is 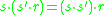for , 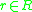(in a more formal language, 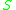is a 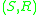-bimoduleBimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
),
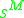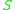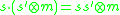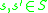inherits a left action of . It is given by for and 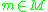. This module is said to be obtained from 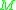through extension of scalars.Informally, extension of scalars is "the tensor product of a ring and a module"; more formally, it is a special case of a tensor product of a bimodule and a module – the tensor product of an
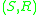bimodule with an R-module is an S-module.Examples
One of the simplest examples is complexificationComplexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
, which is extension of scalars from the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s to the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. More generally, given any field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
K < L, one can extend scalars from K to L. In the language of fields, as module over a field is called a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, and thus extension of scalars converts a vector space over K to a vector space over L. This can also be done for division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
s, as is done in quaternionification (extension from the reals to the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s).
More generally, given an homomorphism from a field or commutative ring R to a ring S, the ring S can be thought of as an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over R, and thus when one extends scalars on an R-module, the resulting module can be thought of alternatively as an S-module, or as an R-module with an algebra representation of S (as an R-algebra). For example, the result of complexifying a real vector space (R = R, S = C) can be interpreted either as a complex vector space (S-module) or as a real vector space with a linear complex structure
Linear complex structure
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.Complex structures have...
(algebra representation of S as an R-module).
Applications
This generalization is useful even for the study of fields – notably, many algebraic objects associated to a field are not themselves fields, but are instead rings, such as algebras over a field, as in representation theoryRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
. Just as one can extend scalars on vector spaces, one can also extend scalars on group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
s and also on modules over group algebras, i.e., group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s. Particularly useful is relating how irreducible representations change under extension of scalars – for example, the representation of the cyclic group of order 4, given by rotation of the plane by 90°, is an irreducible 2-dimensional real representation, but on extension of scalars to the complex numbers, it split into 2 complex representations of dimension 1. This corresponds to the fact that the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of this operator,
is irreducible of degree 2 over the reals, but factors into 2 factors of degree 1 over the complex numbers – it has no real eigenvalues, but 2 complex eigenvalues.Interpretation as a functor
Extension of scalars can be interpreted as a functor from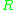-modules to -modules. It sends to 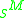, as above, and an -homomorphism 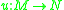to the 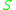-homomorphism 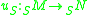defined by 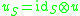.Connection with restriction of scalars
Consider an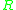-module 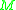and an -module . Given a homomorphism 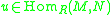, where 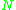is viewed as an 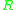-module via restriction of scalarsRestriction of scalars
In abstract algebra, restriction of scalars is a procedure of creating a module over a ring R from a module over another ring S, given a homomorphism f : R \to S between them...
, define
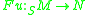to be the compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
,where the last map is
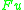. This is an 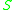-homomorphism, and hence 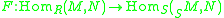is well-defined, and is a homomorphism (of abelian groupsAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
).
In case both
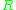and 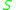have an identity, there is an inverse homomorphism 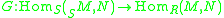, which is defined as follows. Let 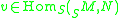. Then 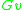is the composition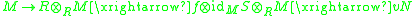,where the first map is the canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
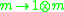.This construction shows that the groups
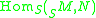and 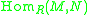are isomorphic. Actually, this isomorphism depends only on the homomorphism 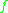, and so is functorial. In the language of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the extension of scalars functor is left adjoint to the restriction of scalars functor.