Tensor algebra
Encyclopedia
In mathematics
, the tensor algebra of a vector space
V, denoted T(V) or T•(V), is the algebra
of tensor
s on V (of any rank) with multiplication being the tensor product
. It is the free algebra
on V, in the sense of being left adjoint to the forgetful functor
from algebras to vector spaces: it is the "most general" algebra containing V, in the sense of the corresponding universal property
(see below).
The tensor algebra also has two coalgebra structures; one simple one, which does not make it a bialgebra, and a more complicated one, which yields a bialgebra
, and can be extended with an antipode to a Hopf algebra
structure.
Note: In this article, all algebras are assumed to be unital and associative
.
over a field
K. For any nonnegative integer
k, we define the kth tensor power of V to be the tensor product
of V with itself k times: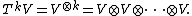
That is, TkV consists of all tensors on V of rank k. By convention T0V is the ground field K (as a one-dimensional vector space over itself).
We then construct T(V) as the direct sum of TkV for k = 0,1,2,…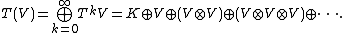
The multiplication in T(V) is determined by the canonical isomorphism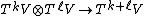
given by the tensor product, which is then extended by linearity to all of T(V). This multiplication rule implies that the tensor algebra T(V) is naturally a graded algebra
with TkV serving as the grade-k subspace. This grading can be extended to a Z grading by appending subspaces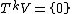
for negative integers k.
The construction generalizes in straightforward manner to the tensor algebra of any module
M over a commutative ring
. If R is a non-commutative ring
, one can still perform the construction for any R-R bimodule
M. (It does not work for ordinary R-modules because the iterated tensor products cannot be formed.)
on the vector space V, and is functorial. As with other free constructions
, the functor T is left adjoint to some forgetful functor. In this case, it's the functor which sends each K-algebra to its underlying vector space.
Explicitly, the tensor algebra satisfies the following universal property
, which formally expresses the statement that it is the most general algebra containing V:
Here i is the canonical inclusion of V into T(V) (the unit of the adjunction). One can, in fact, define the tensor algebra T(V) as the unique algebra satisfying this property (specifically, it is unique up to
a unique isomorphism), but one must still prove that an object satisfying this property exists.
The above universal property shows that the construction of the tensor algebra is functorial in nature. That is, T is a functor
from the K-Vect, category of vector spaces
over K, to K-Alg, the category of K-algebras. The functoriality of T means that any linear map from V to W extends uniquely to an algebra homomorphism from T(V) to T(W).
, the distributive law and K-linearity).
Note that the algebra of polynomials on V is not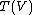
, but rather 
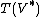: a (homogeneous) linear function on V is an element of 
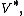for example coordinates 
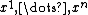on a vector space are covectors, as they take in a vector and give out a scalar (the given coordinate of the vector).
s of T(V). Examples of this are the exterior algebra
, the symmetric algebra
, Clifford algebra
s and universal enveloping algebra
s.
structure on the tensor algebra is given as follows. The coproduct Δ is defined by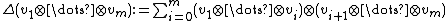
extended by linearity to all of TV. The counit is given by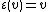
for every 
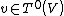and
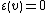for every 
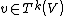for every 
.
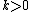Note that Δ : TV → TV ⊗ TV respects the grading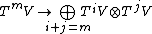
and ε is also compatible with the grading.
The tensor algebra is not a bialgebra
with this coproduct.
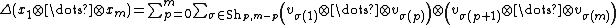
where the summation is taken over all (p,m-p)-shuffles.
Finally, the tensor algebra becomes a Hopf algebra
with antipode given by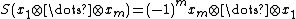
extended linearly to all of TV.
This is just the standard Hopf algebra structure on a free algebra, where one defines the comultiplication on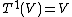
by
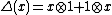
and then extends to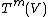
via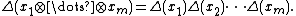
Similarly one defines the antipode on
by
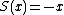
and then extends the antipode as the unique antiautomorphism of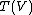
with this property, i.e. we define the antipode on 
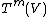via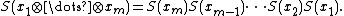
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the tensor algebra of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V, denoted T(V) or T•(V), is the algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
of tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s on V (of any rank) with multiplication being the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
. It is the free algebra
Free algebra
In mathematics, especially in the area of abstract algebra known as ring theory, a free algebra is the noncommutative analogue of a polynomial ring .-Definition:...
on V, in the sense of being left adjoint to the forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
from algebras to vector spaces: it is the "most general" algebra containing V, in the sense of the corresponding universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
(see below).
The tensor algebra also has two coalgebra structures; one simple one, which does not make it a bialgebra, and a more complicated one, which yields a bialgebra
Bialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
, and can be extended with an antipode to a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
structure.
Note: In this article, all algebras are assumed to be unital and associative
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
.
Construction
Let V be a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K. For any nonnegative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
k, we define the kth tensor power of V to be the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of V with itself k times:
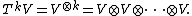
That is, TkV consists of all tensors on V of rank k. By convention T0V is the ground field K (as a one-dimensional vector space over itself).
We then construct T(V) as the direct sum of TkV for k = 0,1,2,…
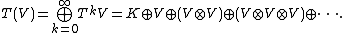
The multiplication in T(V) is determined by the canonical isomorphism
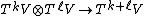
given by the tensor product, which is then extended by linearity to all of T(V). This multiplication rule implies that the tensor algebra T(V) is naturally a graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
with TkV serving as the grade-k subspace. This grading can be extended to a Z grading by appending subspaces
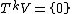for negative integers k.The construction generalizes in straightforward manner to the tensor algebra of any module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
M over a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. If R is a non-commutative ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, one can still perform the construction for any R-R bimodule
Bimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
M. (It does not work for ordinary R-modules because the iterated tensor products cannot be formed.)
Adjunction and universal property
The tensor algebra T(V) is also called the free algebraFree algebra
In mathematics, especially in the area of abstract algebra known as ring theory, a free algebra is the noncommutative analogue of a polynomial ring .-Definition:...
on the vector space V, and is functorial. As with other free constructions
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
, the functor T is left adjoint to some forgetful functor. In this case, it's the functor which sends each K-algebra to its underlying vector space.
Explicitly, the tensor algebra satisfies the following universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
, which formally expresses the statement that it is the most general algebra containing V:
- Any linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
f : V → A from V to an algebra A over K can be uniquely extended to an algebra homomorphismAlgebra homomorphismA homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
from T(V) to A as indicated by the following commutative diagramCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
Here i is the canonical inclusion of V into T(V) (the unit of the adjunction). One can, in fact, define the tensor algebra T(V) as the unique algebra satisfying this property (specifically, it is unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a unique isomorphism), but one must still prove that an object satisfying this property exists.
The above universal property shows that the construction of the tensor algebra is functorial in nature. That is, T is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the K-Vect, category of vector spaces
Category of vector spaces
In mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
over K, to K-Alg, the category of K-algebras. The functoriality of T means that any linear map from V to W extends uniquely to an algebra homomorphism from T(V) to T(W).
Non-commutative polynomials
If V has finite dimension n, another way of looking at the tensor algebra is as the "algebra of polynomials over K in n non-commuting variables". If we take basis vectors for V, those become non-commuting variables (or indeterminants) in T(V), subject to no constraints (beyond associativityAssociativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, the distributive law and K-linearity).
Note that the algebra of polynomials on V is not
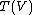, but rather 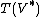: a (homogeneous) linear function on V is an element of 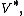for example coordinates 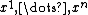on a vector space are covectors, as they take in a vector and give out a scalar (the given coordinate of the vector).Quotients
Because of the generality of the tensor algebra, many other algebras of interest can be constructed by starting with the tensor algebra and then imposing certain relations on the generators, i.e. by constructing certain quotient algebraQuotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
s of T(V). Examples of this are the exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
, the symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
, Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s and universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
s.
Coalgebra structures
The tensor algebra has two coalgebra structures; one simple one, which does not make it a bialgebra, and a more complicated one, which yields a bialgebra, and can be extended with an antipode to a Hopf algebra structure.Simple coalgebra structure
The simple coalgebraCoalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
structure on the tensor algebra is given as follows. The coproduct Δ is defined by
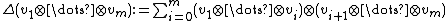
extended by linearity to all of TV. The counit is given by
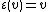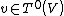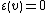for every and for every 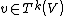for every 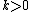.Note that Δ : TV → TV ⊗ TV respects the grading
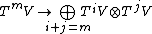
and ε is also compatible with the grading.
The tensor algebra is not a bialgebra
Bialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
with this coproduct.
Bialgebra and Hopf algebra structure
However, the following more complicated coproduct does yield a bialgebra: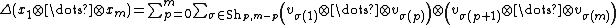where the summation is taken over all (p,m-p)-shuffles.
Finally, the tensor algebra becomes a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
with antipode given by
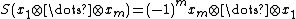
extended linearly to all of TV.
This is just the standard Hopf algebra structure on a free algebra, where one defines the comultiplication on
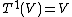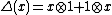
byand then extends to
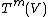via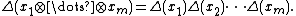Similarly one defines the antipode on
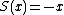
byand then extends the antipode as the unique antiautomorphism of
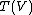with this property, i.e. we define the antipode on 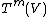via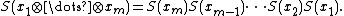See also
- Symmetric algebraSymmetric algebraIn mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
- Exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
- Monoidal categoryMonoidal categoryIn mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
- Stanisław Lem's Love and Tensor Algebra