
Trifocal tensor
Encyclopedia
In computer vision
, the trifocal tensor (also tritensor) is a 3×3×3 array of numbers
(i.e., a tensor
) that incorporates all projective
geometric relationships
among three views. It relates the coordinates of corresponding points or lines in three views, being
independent of the scene structure and depending only on the relative motion (i.e., pose) among the
three views and their intrinsic calibration parameters. Hence, the trifocal tensor can be considered as
the generalization of the fundamental matrix in three views.
It is noted that despite that the tensor is made up of 27 elements, only 18 of them are actually independent.
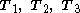 known as its correlation slices.
known as its correlation slices.
Assuming that the projection matrices
of tree views are
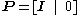 and
and
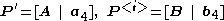 ,
,
the correlation slices of the corresponding tensor can be expressed in closed form as
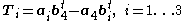 ,
,
where
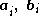
are respectively the ith columns of the camera matrices.
In practice, however, the tensor is estimated from point and line matches across the three views.
lines and points in three images. More specifically, for triplets of corresponding points
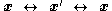
and any corresponding lines
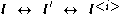 through
through
them, the following trilinear constraints hold: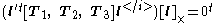
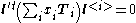
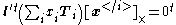
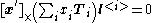
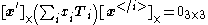
where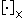 denotes the skew-symmetric cross product matrix.
denotes the skew-symmetric cross product matrix.
location of the point in the third view without any further information. This is known as point transfer and a
similar result holds for lines.
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, the trifocal tensor (also tritensor) is a 3×3×3 array of numbers
(i.e., a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
) that incorporates all projective
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
geometric relationships
among three views. It relates the coordinates of corresponding points or lines in three views, being
independent of the scene structure and depending only on the relative motion (i.e., pose) among the
three views and their intrinsic calibration parameters. Hence, the trifocal tensor can be considered as
the generalization of the fundamental matrix in three views.
It is noted that despite that the tensor is made up of 27 elements, only 18 of them are actually independent.
Correlation slices
The tensor can also be seen as a collection of three rank-two 3 x 3 matrices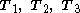 known as its correlation slices.
known as its correlation slices.Assuming that the projection matrices
Camera matrix
In computer vision a camera matrix or projection matrix is a 3 \times 4 matrix which describes the mapping of a pinhole camera from 3D points in the world to 2D points in an image....
of tree views are
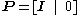 and
and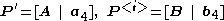 ,
,the correlation slices of the corresponding tensor can be expressed in closed form as
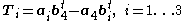 ,
,where
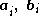
are respectively the ith columns of the camera matrices.
In practice, however, the tensor is estimated from point and line matches across the three views.
Trilinear constraints
One of the most important properties of the trifocal tensor is that it gives rise to linear relationships betweenlines and points in three images. More specifically, for triplets of corresponding points
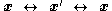
and any corresponding lines
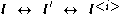 through
throughthem, the following trilinear constraints hold:
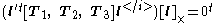
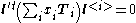
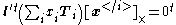
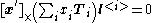
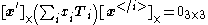
where
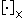 denotes the skew-symmetric cross product matrix.
denotes the skew-symmetric cross product matrix.Transfer
Given the trifocal tensor of three views and a pair of matched points in two views, it is possible to determine thelocation of the point in the third view without any further information. This is known as point transfer and a
similar result holds for lines.
External links
- Visualization of trifocal geometry (originally by Sylvain Bougnoux of INRIA Robotvis, requires JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
)

