Nisnevich topology
Encyclopedia
In algebraic geometry
, the Nisnevich topology, sometimes called the completely decomposed topology, is a Grothendieck topology
on the category of scheme
s which has been used in algebraic K-theory
, A¹ homotopy theory
, and the theory of motive
s. It was originally introduced by Yevsey Nisnevich, who was motivated by the theory of adeles
.
such that for every (possibly non-closed) point x ∈ X, there exists a point y ∈ Y such that the induced map of residue field
s k(x) → k(y) is an isomorphism. Equivalently, f must be flat, unramified, locally of finite presentation, and for every point x ∈ X, there must exist a point y in the fiber such that k(x) → k(y) is an isomorphism.
A family of morphisms {uα : Xα → X} is a Nisnevich cover if the family is jointly surjective and each uα is a Nisnevich morphism. The Nisnevich covers are the covering families of a pretopology on the category of schemes and morphisms of schemes. This generates a topology called the Nisnevich topology. The category of schemes with the Nisnevich topology is notated Nis.
The small Nisnevich site of X is the category O(XNis) whose objects are schemes U with a fixed Nisnevich morphism U → X. The morphisms are morphisms of schemes compatible with the fixed maps to X. The big Nisnevich site of X is the category Nis/X, that is, the category of schemes with a fixed map to X, considered with the Nisnevich topology.
The Nisnevich topology has several variants which are adapted to studying singular varieties. Covers in these topologies include resolutions of singularities
or weaker forms of resolution.
The cdh and l′ topologies are incomparable with the étale topology
, and the qfh topology is finer than the étale topology.
and Jean-Pierre Serre
which states that a rationally trivial torsor is locally trivial in the Zariski topology
. One of the key properties of the Nisnevich topology is the existence of a descent spectral sequence
. Let X be a Noetherian scheme of finite Krull dimension. Let Gn(X) denote the Quillen K-groups of the category of coherent sheaves on X, and let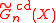
denote the sheavings of these groups with respect to the Nisnevich topology. Then there is a convergent spectral sequence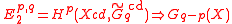
for , , and . If
is a prime number not equal to the characteristic of X, then there is an analogous convergent spectral sequence for K-groups with coefficients in 
.
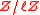The Nisnevich topology has also found important applications in algebraic K-theory
, A¹ homotopy theory
and the theory of motive
s.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the Nisnevich topology, sometimes called the completely decomposed topology, is a Grothendieck topology
Grothendieck topology
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C which makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.Grothendieck topologies axiomatize the notion...
on the category of scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
s which has been used in algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
, A¹ homotopy theory
A¹ homotopy theory
In algebraic geometry and algebraic topology, a branch of mathematics, A1 homotopy theory is a way to apply the techniques of algebraic topology, specifically homotopy, to algebraic varieties and, more generally, to schemes. The theory is due to Fabien Morel and Vladimir Voevodsky...
, and the theory of motive
Motive (algebraic geometry)
In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
s. It was originally introduced by Yevsey Nisnevich, who was motivated by the theory of adeles
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
.
Definition
A morphism of schemes is called a Nisnevich morphism if it is an étale morphismÉtale morphism
In algebraic geometry, a field of mathematics, an étale morphism is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem, but because open sets in the Zariski topology are so large, they are not...
such that for every (possibly non-closed) point x ∈ X, there exists a point y ∈ Y such that the induced map of residue field
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
s k(x) → k(y) is an isomorphism. Equivalently, f must be flat, unramified, locally of finite presentation, and for every point x ∈ X, there must exist a point y in the fiber such that k(x) → k(y) is an isomorphism.
A family of morphisms {uα : Xα → X} is a Nisnevich cover if the family is jointly surjective and each uα is a Nisnevich morphism. The Nisnevich covers are the covering families of a pretopology on the category of schemes and morphisms of schemes. This generates a topology called the Nisnevich topology. The category of schemes with the Nisnevich topology is notated Nis.
The small Nisnevich site of X is the category O(XNis) whose objects are schemes U with a fixed Nisnevich morphism U → X. The morphisms are morphisms of schemes compatible with the fixed maps to X. The big Nisnevich site of X is the category Nis/X, that is, the category of schemes with a fixed map to X, considered with the Nisnevich topology.
The Nisnevich topology has several variants which are adapted to studying singular varieties. Covers in these topologies include resolutions of singularities
Resolution of singularities
In algebraic geometry, the problem of resolution of singularities asks whether every algebraic variety V has a resolution, a non-singular variety W with a proper birational map W→V...
or weaker forms of resolution.
- The cdh topology allows proper birational morphisms as coverings.
- The qfh topology allows De Jong's alterations as coverings.
- The l′ topology allows morphisms as in the conclusion of Gabber's local uniformization theorem.
The cdh and l′ topologies are incomparable with the étale topology
Étale topology
In algebraic geometry, the étale topology is a Grothendieck topology on the category of schemes which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic...
, and the qfh topology is finer than the étale topology.
Local rings in the Nisnevich topology
If x is a point of a scheme X, then the local ring of x in the Nisnevich topology is the henselization of the local ring of x in the Zariski topology.Applications
Nisnevich introduced his topology to provide a cohomological interpretation of the class set of an affine group scheme, which was originally defined in adelic terms. He used it to partially prove a conjecture of Alexander GrothendieckAlexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
and Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
which states that a rationally trivial torsor is locally trivial in the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
. One of the key properties of the Nisnevich topology is the existence of a descent spectral sequence
Spectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
. Let X be a Noetherian scheme of finite Krull dimension. Let Gn(X) denote the Quillen K-groups of the category of coherent sheaves on X, and let
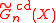denote the sheavings of these groups with respect to the Nisnevich topology. Then there is a convergent spectral sequence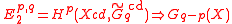for , , and . If
is a prime number not equal to the characteristic of X, then there is an analogous convergent spectral sequence for K-groups with coefficients in 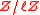.The Nisnevich topology has also found important applications in algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
, A¹ homotopy theory
A¹ homotopy theory
In algebraic geometry and algebraic topology, a branch of mathematics, A1 homotopy theory is a way to apply the techniques of algebraic topology, specifically homotopy, to algebraic varieties and, more generally, to schemes. The theory is due to Fabien Morel and Vladimir Voevodsky...
and the theory of motive
Motive (algebraic geometry)
In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
s.