Systems of polynomial equations
Encyclopedia
A system of polynomial equations is a set of simultaneous equations
f1 = 0, ..., fh = 0 where the fi are polynomials
in several variables, say x1, ..., xn, over some field
k.
Usually, the field k is either the field of rational number
s or a finite field
, although most of the theory applies to any field.
A solution is a set of the values for the xi which belong to some algebraically closed field extension
K of k. When k is the field of rational number
s, then K is the field of complex number
s.
. Such an equation may be converted into a polynomial system by expanding the sines and cosines in it, replacing sin(x) and cos(x) by two new variables s and c and adding the new equation s2 + c2 − 1 = 0.
For example the equation
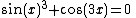
is equivalent to the polynomial system
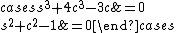
For example, if a system contains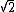
, a system over the rational numbers is obtained by adding the equation r22 − 2 = 0 and replacing 
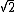by r2 in the other equations.
In the case of a finite field, the same transformation allows always to suppose that the field k has a prime order.
this means that 1 is a linear combination (with polynomials as coefficients) of the first members of the equations. Most but not all overdetermined systems are inconsistent. For example the system x3 − 1 = 0, x2 − 1 = 0 is overdetermined but not inconsistent.
A system is underdetermined if the number of equations is lower than the number of the variables. An underdetermined system is either inconsistent or has infinitely many solutions in an algebraically closed extension K of k.
A system is zero-dimensional if it has a finite number of solutions in an algebraically closed extension K of k. This terminology comes from the fact that the algebraic variety
of the solutions has dimension
zero. A system with infinitely many solutions is said positive-dimensional.
A zero-dimensional system with as many equations as variables is said well-behaved.
Bézout's theorem
asserts that a well-behaved system whose equations have degrees d1, ..., dn has at most d1...dn solutions. This bound is sharp. If all the degrees are equal to d, this bound becomes dn and is exponential in the number of variables.
This exponential behavior makes solving polynomial systems difficult and explains why there are few solvers that are able to automatically solve systems with Bézout's bound higher than, say 25 (three equations of degree 3 or five equations of degree 2 are beyond this bound).
of the left hand side of the equations. The system is inconsistent if this Gröbner basis is reduced to 1. The system is zero-dimensional if, for every variable there is a leading monomial
of some element of the Gröbner basis which is a pure power of this variable. For this test, the best monomial order is usually the graded reverse lexicographic one (grevlex).
If the system is positive-dimensional, it has infinitely many solutions. It is thus not possible to enumerate them. It follows that, in this case, solving may only mean "finding a description of the solutions from which the relevant properties of the solutions are easy to extract". There is no commonly accepted such description. In fact there is a lot of different "relevant properties", which involve almost every subfields of algebraic geometry
.
A natural example of an open question about solving positive-dimensional systems is the following: decide if a polynomial system over the rational number
s has a finite number of real solutions and compute them. The only published algorithm which allows to solve this question is cylindrical algebraic decomposition
, which is not efficient enough, in practice, to be used for this.
For zero-dimensional systems, solving consists in computing all the solutions. There are two different ways of outputting the solutions. The most common, possible only for real or complex solutions consists in outputting numeric approximations of the solutions. Such a solution is said numeric. A solution is certified if it is provided with a bound on the error of the approximations which separates the different solutions.
The other way to represent the solutions is said algebraic. It uses the fact that, for a zero-dimensional system, the solutions belong to the algebraic closure
of the field k of the coefficients of the system. There are several ways to represent the solution in an algebraic closure, which are discussed below. All of them allow to compute a numerical approximation of the solutions by solving one or several univariate equations. For this computation, the representation of the solutions which need only to solve only one univariate polynomial for each solution have to be preferred: computing the roots of a polynomial which has approximate coefficients is a highly unstable problem.
s. Such a chain consists in a sequence of polynomials f1(x1), f2(x1, x2), ..., fn(x1, ..., xn) such that, for every i such that 1 ≤ i ≤ n
To such a regular chain
is associated a triangular system of equations
The solutions of this system are obtained by solving the first univariate equations, substitute the solutions in the other equations, then solving the second equation which is now univariate, and so on. The definition of regular chains implies that the univariate equation obtained from fi has degree di and thus that this system has d1 ... dn solutions, provided that there is no multiple root in this resolution process (fundamental theorem of algebra
).
Every zero-dimensional system of polynomial equations is equivalent (i.e. has the same solutions) to a finite number of regular chains. Several regular chains may be needed, as it is the case for the following system which has three solutions.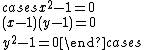
There are severals algorithms for computing a triangular decomposition
of an arbitrary polynomial system (not necessarily zero-dimensional) into regular chain
s (or regular semi-algebraic system
s).
There is also an algorithm which is specific to the zero-dimensional case and is competitive, in this case, with the direct algorithms. It consists in computing first the Gröbner basis
for the graded reverse lexicographic order (grevlex), then deducing the Gröbner basis by FGLM algorithm and finally applying Lextriangular algorithm.
This representation of the solutions and the algorithms to compute it are presently a very efficient way in practice for solving zero-dimensional polynomial systems with coefficients in a finite field.
For rational coefficients, the Lextriangular algorithm has two drawbacks:
Algorithms computing triangular decomposition
s directly (that is, without precomputing a
Gröbner Basis) do not have the above drawback related to size output. Actually, for a given polynomial system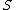
whose solutions can be described by a single regular chain, there exists one regular chain representing 
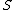in a nearly optimal way in term of size.
In order to address the above drawback related to numerical evaluation, one can take advantage of the rational univariate representation, which follows.
A RUR of a zero-dimensional system consists in a linear combination x0 of the variables, called separating variable, and a system of equations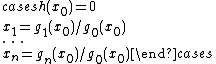
where h is a univariate polynomial in x0 of degree D and g0, ..., gn are univariate polynomials in x0 of degree less than D.
Given a zero-dimensional polynomial system over the rational numbers, the RUR has the following properties.
For example, for above system, every linear combination of the variable, except the multiples of x, y and x + y, is a separating variable. If one choose t = (x − y)/2 as separating variable, then the RUR is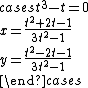
The RUR is uniquely defined independently of any algorithm. On the contrary, a triangular decomposition of a zero-dimensional system is not uniquely defined. However, among all triangular decompositions of a given zero-dimensional system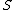
, there is one which is defined independently of any algorithm: the equiprojectable decomposition of 
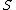. For this latter, as for the RUR, sharp bounds are available for the coefficients. Consequently, efficient algorithms, based on so-called modular methods, exist for computing the equiprojectable decomposition and the RUR.
On the computational point of view, there is one main difference between the equiprojectable decomposition and the RUR. The latter has the conceptual advantage of reducing the numeric computation of the solutions to computing the roots of a single univariate polynomial and substituting in some rational functions. However, when the equiprojectable decomposition has more than one component, the coefficients of its polynomials are generally smaller than those appearing in the RUR.
As the definition of the RUR involves divisions by D, the RUR is not defined over fields of non zero characteristic
, whereas triangular decomposition
techniques are available over any fields.
work also for polynomial systems. However the specific methods will generally be preferred, as the general methods generally do not allow to find all solutions. Especially, when a general method does not find any solution, this is usually not an indication that there is no solution.
Nevertheless two methods deserve to be mentioned here.
Newton's method
may be used if the number of equations is equal to the number of variables. It does not allow to find all the solutions not to prove that there is no solution. But it is very fast when starting from a point which is close to a solution. Therefore it is a basic tool for Homotopy Continuation method described below.
Optimization
is rarely used for solving polynomial systems, but it succeeded, around 1970, to show that a system of 81 quadratic equations in 56 variables is not inconsistent. With the other known methods this system remains beyond the possibilities of modern technology. This method consists simply in minimizing the sum of the squares of the equations. If zero is found as a local minimum, then it is attained at a solution. This method works for overdetermined systems, but outputs an empty information if all local minimums which are found are positive.
This method divides into three steps. First an upper bound on the number of solutions is computed. This bound has to be as sharp as possible. Therefore it is computed by, at least, four different methods and the best value, say N, is kept.
In the second step, a system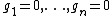
of polynomial equations is generated which has exactly N solutions that are easy to compute. This new system has the same number n of variables and the same number n of equations and the same general structure as the system to solve, 
.
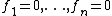Then a homotopy
between the two systems is considered. It consists, for example, of the straight line between the two systems, but other paths may be considered, in particular to avoid some singularities, in the system
.
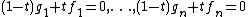The homotopy continuation consists in deforming the parameter t from 0 to 1 and following the N solutions during this deformation. This gives the desired solutions for t = 1. Following means that, if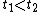
, the solutions for 
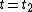are deduced from the solutions for 
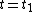by Newton's method. The difficulty here is to well choose the value of 
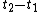: Too large, Newton's convergence may be slow and may even jump from a solution path to another one. Too small, and the number of steps slows down the method.
The roots of the univariate polynomial have thus to be computed at a high precision which may not be defined once for all. There are two algorithms which fulfill this requirement.
The Maple
function RootFinding[Isolate] takes as input any polynomial system over the rational numbers (if some coefficients are floating point
numbers, they are converted to rational numbers) and outputs the real solutions represented either (optionally) as intervals of rational numbers or as floating point approximations of arbitrary precision. If the system is not zero dimensional, this is signaled as an error.
Internally, this solver, designed by F. Rouillier computes first a Gröbner basis and then a Rational Univariate Representation from which the required approximation of the solutions are deduced. It works routinely for systems having up to a few hundred complex solutions.
The rational univariate representation may be computed with Maple
function Groebner[RationalUnivariateRepresentation].
To extract all the complex solutions from a rational univariate representation, one may use MPSolve
, which computes the complex roots of univariate polynomials to any precision. It is recommended to run MPSolve
several times, doubling the precision each time, until solutions remain stable, as the substitution of the roots in the equations of the input variables can be highly unstable.
The second solver is PHCpack, written under the direction of J. Verschelde. PHCpack implements the homotopy continuation method.
This solver computes the isolated complex solutions of polynomial systems having as many equations as variables.
The third solver is the Maple
command RegularChains[RealTriangularize]. For any zero-dimensional input system with rational number coefficients it returns those solutions whose coordinates are real algebraic numbers. Each of these real numbers is encoded by an isolation interval and a defining polynomial.
The command RegularChains[RealTriangularize] is part of the Maple
library RegularChains
, written by Marc Moreno-Maza, his students and post-doctoral fellows (listed in chronological order of graduation) Francois Lemaire, Yuzhen Xie, Xin Li, Xiao Rong, Liyun Li, Wei Pan and Changbo Chen. Other contributors are Eric Schost, Bican Xia and Wenyuan Wu. This library provides a large set of functionalities for solving zero-dimensional and positive dimensional systems. In both cases, for input systems with rational number coefficients, routines for isolating the real solutions are available. For arbitrary input system of polynomial equations and inequations (with rational number coefficients or with coefficients in a prime field) one can use the command RegularChains[Triangularize] for computing the solutions whose coordinates are in the algebraic closure of the coefficient field. The underlying algorithms are based on the notion of a regular chain
.
While the command RegularChains[RealTriangularize] is currently limited to zero-dimensional systems, a future release will be able to process any system of polynomial equations, inequations and inequalities. The corresponding new algorithm is based on the concept of a regular semi-algebraic system
.
Simultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
f1 = 0, ..., fh = 0 where the fi are polynomials
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
in several variables, say x1, ..., xn, over some field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k.
Usually, the field k is either the field of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s or a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, although most of the theory applies to any field.
A solution is a set of the values for the xi which belong to some algebraically closed field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
K of k. When k is the field of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, then K is the field of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Trigonometric equations
A trigonometric equation is an equation g = 0 where g is a trigonometric polynomialTrigonometric polynomial
In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin and cos with n a natural number. The coefficients may be taken as real numbers, for real-valued functions...
. Such an equation may be converted into a polynomial system by expanding the sines and cosines in it, replacing sin(x) and cos(x) by two new variables s and c and adding the new equation s2 + c2 − 1 = 0.
For example the equation
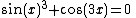
is equivalent to the polynomial system
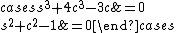
Solutions in a finite field
When solving a system over a finite field k with q elements, one is primarily interested in the solutions in k. As the elements of k are exactly the solutions of the equation xq − x = 0, it suffices, for restricting the solutions to k, to add the equation xiq − xi = 0 for each variable xi.Coefficients in a number field or in a finite field with non-prime order
The elements of a number field are usually represented as polynomials in a generator of the field which satisfies some univariate polynomial equation. To work with a polynomial system whose coefficients belong to a number field, it suffices to consider this generator as a new variable and to add the equation of the generator to the equations of the system. Thus solving a polynomial system over a number field is reduced to solving another system over the rational numbers.For example, if a system contains
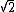, a system over the rational numbers is obtained by adding the equation r22 − 2 = 0 and replacing 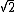by r2 in the other equations.In the case of a finite field, the same transformation allows always to suppose that the field k has a prime order.
Basic properties and definitions
A system is overdetermined if the number of equations is higher than the number of variables. A system is inconsistent if it has no solutions. By Hilbert's NullstellensatzHilbert's Nullstellensatz
Hilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...
this means that 1 is a linear combination (with polynomials as coefficients) of the first members of the equations. Most but not all overdetermined systems are inconsistent. For example the system x3 − 1 = 0, x2 − 1 = 0 is overdetermined but not inconsistent.
A system is underdetermined if the number of equations is lower than the number of the variables. An underdetermined system is either inconsistent or has infinitely many solutions in an algebraically closed extension K of k.
A system is zero-dimensional if it has a finite number of solutions in an algebraically closed extension K of k. This terminology comes from the fact that the algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
of the solutions has dimension
Dimension of an algebraic variety
In mathematics, the dimension of an algebraic variety V in algebraic geometry is defined, informally speaking, as the number of independent rational functions that exist on V.For example, an algebraic curve has by definition dimension 1...
zero. A system with infinitely many solutions is said positive-dimensional.
A zero-dimensional system with as many equations as variables is said well-behaved.
Bézout's theorem
Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
asserts that a well-behaved system whose equations have degrees d1, ..., dn has at most d1...dn solutions. This bound is sharp. If all the degrees are equal to d, this bound becomes dn and is exponential in the number of variables.
This exponential behavior makes solving polynomial systems difficult and explains why there are few solvers that are able to automatically solve systems with Bézout's bound higher than, say 25 (three equations of degree 3 or five equations of degree 2 are beyond this bound).
What is solving?
The first thing to do for solving a polynomial system is to decide if it is inconsistent, zero-dimensional or positive dimensional. This may be done by the computation of a Gröbner basisGröbner basis
In computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
of the left hand side of the equations. The system is inconsistent if this Gröbner basis is reduced to 1. The system is zero-dimensional if, for every variable there is a leading monomial
Gröbner basis
In computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
of some element of the Gröbner basis which is a pure power of this variable. For this test, the best monomial order is usually the graded reverse lexicographic one (grevlex).
If the system is positive-dimensional, it has infinitely many solutions. It is thus not possible to enumerate them. It follows that, in this case, solving may only mean "finding a description of the solutions from which the relevant properties of the solutions are easy to extract". There is no commonly accepted such description. In fact there is a lot of different "relevant properties", which involve almost every subfields of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
A natural example of an open question about solving positive-dimensional systems is the following: decide if a polynomial system over the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s has a finite number of real solutions and compute them. The only published algorithm which allows to solve this question is cylindrical algebraic decomposition
Cylindrical algebraic decomposition
Given a set of polynomials in Rn and a set S in Rn the Cylindrical algebraic decomposition algorithm finds a decomposition of S in to a number of cells such that for each cell each polynomial has constant sign.-References:...
, which is not efficient enough, in practice, to be used for this.
For zero-dimensional systems, solving consists in computing all the solutions. There are two different ways of outputting the solutions. The most common, possible only for real or complex solutions consists in outputting numeric approximations of the solutions. Such a solution is said numeric. A solution is certified if it is provided with a bound on the error of the approximations which separates the different solutions.
The other way to represent the solutions is said algebraic. It uses the fact that, for a zero-dimensional system, the solutions belong to the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of the field k of the coefficients of the system. There are several ways to represent the solution in an algebraic closure, which are discussed below. All of them allow to compute a numerical approximation of the solutions by solving one or several univariate equations. For this computation, the representation of the solutions which need only to solve only one univariate polynomial for each solution have to be preferred: computing the roots of a polynomial which has approximate coefficients is a highly unstable problem.
Regular chains
The usual way of representing the solutions is through zero-dimensional regular chainRegular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
s. Such a chain consists in a sequence of polynomials f1(x1), f2(x1, x2), ..., fn(x1, ..., xn) such that, for every i such that 1 ≤ i ≤ n
- fi is a polynomial in x1, ..., xi only, which has a degree di > 0 in xi ;
- the coefficient of xidi in fi is a polynomial in x1, ..., xi − 1 which does not have any common zero with f1, ..., fi − 1.
To such a regular chain
Regular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
is associated a triangular system of equations
The solutions of this system are obtained by solving the first univariate equations, substitute the solutions in the other equations, then solving the second equation which is now univariate, and so on. The definition of regular chains implies that the univariate equation obtained from fi has degree di and thus that this system has d1 ... dn solutions, provided that there is no multiple root in this resolution process (fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
).
Every zero-dimensional system of polynomial equations is equivalent (i.e. has the same solutions) to a finite number of regular chains. Several regular chains may be needed, as it is the case for the following system which has three solutions.
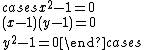
There are severals algorithms for computing a triangular decomposition
Triangular decomposition
In computer algebra, a triangular decomposition of a polynomial system S is a set of simpler polynomial systems S_1,\ldots, S_e such that a point is a solution of S if and only if it is a solution of one of the systems S_1,\ldots, S_e....
of an arbitrary polynomial system (not necessarily zero-dimensional) into regular chain
Regular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
s (or regular semi-algebraic system
Regular semi-algebraic system
In computer algebra, a regular semi-algebraic system is a particular kind of triangular system of multivariate polynomials over a real closed field.- Introduction :...
s).
There is also an algorithm which is specific to the zero-dimensional case and is competitive, in this case, with the direct algorithms. It consists in computing first the Gröbner basis
Gröbner basis
In computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
for the graded reverse lexicographic order (grevlex), then deducing the Gröbner basis by FGLM algorithm and finally applying Lextriangular algorithm.
This representation of the solutions and the algorithms to compute it are presently a very efficient way in practice for solving zero-dimensional polynomial systems with coefficients in a finite field.
For rational coefficients, the Lextriangular algorithm has two drawbacks:
- The output uses to involve huge integers which may make the computation and the use of the result problematic.
- To deduce the numeric values of the solutions from the output, one has to solve univariate polynomials with approximate coefficients, which is a highly unstable problem.
Algorithms computing triangular decomposition
Triangular decomposition
In computer algebra, a triangular decomposition of a polynomial system S is a set of simpler polynomial systems S_1,\ldots, S_e such that a point is a solution of S if and only if it is a solution of one of the systems S_1,\ldots, S_e....
s directly (that is, without precomputing a
Gröbner Basis) do not have the above drawback related to size output. Actually, for a given polynomial system
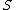whose solutions can be described by a single regular chain, there exists one regular chain representing 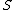in a nearly optimal way in term of size.In order to address the above drawback related to numerical evaluation, one can take advantage of the rational univariate representation, which follows.
Rational Univariate Representation
The Rational Univariate Representation or RUR is a representation of the solutions of a zero-dimensional polynomial system over the rational numbers which has been introduced by M.F. Roy, F. Rouillier and L. Gonzales-Vega for remedying to the above drawbacks of the regular chain representation.A RUR of a zero-dimensional system consists in a linear combination x0 of the variables, called separating variable, and a system of equations
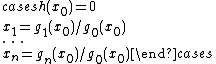
where h is a univariate polynomial in x0 of degree D and g0, ..., gn are univariate polynomials in x0 of degree less than D.
Given a zero-dimensional polynomial system over the rational numbers, the RUR has the following properties.
- All but a finite number linear combinations of the variables are separating variables.
- When the separating variable is chosen, the RUR exists and is unique. In particular h and the gi are defined independently of any algorithm to compute them.
- The solutions of the system are in one to one correspondence with the roots of h and the multiplicityMultiplicity (mathematics)In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
of each root of h equals the multiplicity of the corresponding solution. - The solutions of the system are obtained by substituting the roots of h in the other equations.
- If h does not have any multiple root then g0 is the derivative of h.
For example, for above system, every linear combination of the variable, except the multiples of x, y and x + y, is a separating variable. If one choose t = (x − y)/2 as separating variable, then the RUR is
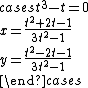
The RUR is uniquely defined independently of any algorithm. On the contrary, a triangular decomposition of a zero-dimensional system is not uniquely defined. However, among all triangular decompositions of a given zero-dimensional system
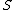, there is one which is defined independently of any algorithm: the equiprojectable decomposition of 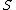. For this latter, as for the RUR, sharp bounds are available for the coefficients. Consequently, efficient algorithms, based on so-called modular methods, exist for computing the equiprojectable decomposition and the RUR.On the computational point of view, there is one main difference between the equiprojectable decomposition and the RUR. The latter has the conceptual advantage of reducing the numeric computation of the solutions to computing the roots of a single univariate polynomial and substituting in some rational functions. However, when the equiprojectable decomposition has more than one component, the coefficients of its polynomials are generally smaller than those appearing in the RUR.
As the definition of the RUR involves divisions by D, the RUR is not defined over fields of non zero characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
, whereas triangular decomposition
Triangular decomposition
In computer algebra, a triangular decomposition of a polynomial system S is a set of simpler polynomial systems S_1,\ldots, S_e such that a point is a solution of S if and only if it is a solution of one of the systems S_1,\ldots, S_e....
techniques are available over any fields.
General solving algorithms
The general numerical algorithms which are designed for any system of simultaneous equationsSimultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
work also for polynomial systems. However the specific methods will generally be preferred, as the general methods generally do not allow to find all solutions. Especially, when a general method does not find any solution, this is usually not an indication that there is no solution.
Nevertheless two methods deserve to be mentioned here.
Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
may be used if the number of equations is equal to the number of variables. It does not allow to find all the solutions not to prove that there is no solution. But it is very fast when starting from a point which is close to a solution. Therefore it is a basic tool for Homotopy Continuation method described below.
Optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
is rarely used for solving polynomial systems, but it succeeded, around 1970, to show that a system of 81 quadratic equations in 56 variables is not inconsistent. With the other known methods this system remains beyond the possibilities of modern technology. This method consists simply in minimizing the sum of the squares of the equations. If zero is found as a local minimum, then it is attained at a solution. This method works for overdetermined systems, but outputs an empty information if all local minimums which are found are positive.
Homotopy continuation method
This is a semi-numeric method which supposes that the number of equations is equal to the number of variables. This method is relatively old but it has been dramatically improved in the last decades by J. Verschelde and people around him.This method divides into three steps. First an upper bound on the number of solutions is computed. This bound has to be as sharp as possible. Therefore it is computed by, at least, four different methods and the best value, say N, is kept.
In the second step, a system
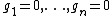of polynomial equations is generated which has exactly N solutions that are easy to compute. This new system has the same number n of variables and the same number n of equations and the same general structure as the system to solve, 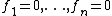.Then a homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
between the two systems is considered. It consists, for example, of the straight line between the two systems, but other paths may be considered, in particular to avoid some singularities, in the system
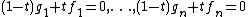.The homotopy continuation consists in deforming the parameter t from 0 to 1 and following the N solutions during this deformation. This gives the desired solutions for t = 1. Following means that, if
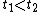, the solutions for 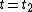are deduced from the solutions for 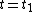by Newton's method. The difficulty here is to well choose the value of 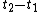: Too large, Newton's convergence may be slow and may even jump from a solution path to another one. Too small, and the number of steps slows down the method.Numerically solving from the Rational Univariate Representation
To deduce the numeric values of the solutions from a RUR seems easy: it suffices to compute the roots of the univariate polynomial and to substitute them in the other equations. This is not so easy because the evaluation of a polynomial at the roots of another polynomial is highly unstable.The roots of the univariate polynomial have thus to be computed at a high precision which may not be defined once for all. There are two algorithms which fulfill this requirement.
- Aberth methodAberth methodThe Aberth method, or Aberth–Ehrlich method, named after Oliver Aberth and Louis W. Ehrlich, is a root-finding algorithm for simultaneous approximation of all the roots of a univariate polynomial....
, implemented in MPSolveMPSolveMPSolve is a package for the approximation of the roots of a univariate polynomial. It uses the Aberth method....
computes all the complex roots to any precision. - Uspensky's algorithm of Collins and Akritas, improved by Rouillier and Zimmermann and based on Descartes' rule of signsDescartes' rule of signsIn mathematics, Descartes' rule of signs, first described by René Descartes in his work La Géométrie, is a technique for determining the number of positive or negative real roots of a polynomial....
. This algorithms computes the real roots, isolated in intervals of arbitrary small width. It is implemented in MapleMaple (software)Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....
(functions fsolve and RootFinding[Isolate]).
Software packages
There are at least three software packages which can solve zero-dimensional systems automatically (by automatically, one means that no human intervention is needed between input and output, and thus that no knowledge of the method by the user is needed). There are also several other software packages which may be useful for solving zero-dimensional systems. Some of them are listed after the automatic solvers.The Maple
Maple (software)
Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....
function RootFinding[Isolate] takes as input any polynomial system over the rational numbers (if some coefficients are floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
numbers, they are converted to rational numbers) and outputs the real solutions represented either (optionally) as intervals of rational numbers or as floating point approximations of arbitrary precision. If the system is not zero dimensional, this is signaled as an error.
Internally, this solver, designed by F. Rouillier computes first a Gröbner basis and then a Rational Univariate Representation from which the required approximation of the solutions are deduced. It works routinely for systems having up to a few hundred complex solutions.
The rational univariate representation may be computed with Maple
Maple (software)
Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....
function Groebner[RationalUnivariateRepresentation].
To extract all the complex solutions from a rational univariate representation, one may use MPSolve
MPSolve
MPSolve is a package for the approximation of the roots of a univariate polynomial. It uses the Aberth method....
, which computes the complex roots of univariate polynomials to any precision. It is recommended to run MPSolve
MPSolve
MPSolve is a package for the approximation of the roots of a univariate polynomial. It uses the Aberth method....
several times, doubling the precision each time, until solutions remain stable, as the substitution of the roots in the equations of the input variables can be highly unstable.
The second solver is PHCpack, written under the direction of J. Verschelde. PHCpack implements the homotopy continuation method.
This solver computes the isolated complex solutions of polynomial systems having as many equations as variables.
The third solver is the Maple
Maple (software)
Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....
command RegularChains[RealTriangularize]. For any zero-dimensional input system with rational number coefficients it returns those solutions whose coordinates are real algebraic numbers. Each of these real numbers is encoded by an isolation interval and a defining polynomial.
The command RegularChains[RealTriangularize] is part of the Maple
Maple (software)
Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....
library RegularChains
RegularChains
The RegularChains package in the computer algebra software package Maple is a collection of commands for solving systems of polynomial equations, inequations and inequalities symbolically....
, written by Marc Moreno-Maza, his students and post-doctoral fellows (listed in chronological order of graduation) Francois Lemaire, Yuzhen Xie, Xin Li, Xiao Rong, Liyun Li, Wei Pan and Changbo Chen. Other contributors are Eric Schost, Bican Xia and Wenyuan Wu. This library provides a large set of functionalities for solving zero-dimensional and positive dimensional systems. In both cases, for input systems with rational number coefficients, routines for isolating the real solutions are available. For arbitrary input system of polynomial equations and inequations (with rational number coefficients or with coefficients in a prime field) one can use the command RegularChains[Triangularize] for computing the solutions whose coordinates are in the algebraic closure of the coefficient field. The underlying algorithms are based on the notion of a regular chain
Regular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
.
While the command RegularChains[RealTriangularize] is currently limited to zero-dimensional systems, a future release will be able to process any system of polynomial equations, inequations and inequalities. The corresponding new algorithm is based on the concept of a regular semi-algebraic system
Regular semi-algebraic system
In computer algebra, a regular semi-algebraic system is a particular kind of triangular system of multivariate polynomials over a real closed field.- Introduction :...
.