Triangular decomposition
Encyclopedia
In computer algebra, a triangular decomposition of a polynomial system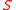 
is a set of simpler polynomial systems 
such that a point is a solution of 
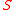if and only if it is a solution of one of the systems 
.
When the purpose is to describe the solution set of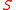
in the algebraic closure
of its coefficient field, those simpler systems are regular chain
s. If the coefficient of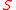
are real numbers, then the real solutions of 
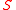can be obtained by a triangular decomposition into regular semi-algebraic system
s. In both cases, each of these simpler systems has a triangular shape and remarkable properties, which justifies the terminology.
be a field and 
be ordered variables. We denote by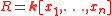 
the corresponding polynomial ring. Let 
be a subset of 
. There are two notions of a triangular decomposition of 
(regarded as a system of polynomial equations) over the algebraic closure
of
. The first one is to decompose lazily, by representing only the generic point
s of the algebraic set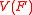
in the so-called sense of Kalkbrener.
The second is to describe explicitly all the points of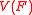
in the so-called sense of in Lazard and Wen-Tsun Wu
.
In both cases
are finitely many regular chain
s of
and 
denotes the radical of the saturated ideal of 
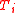while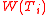 
denotes the quasi-component of 
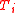. Please refer to regular chain
for definitions of these notions.
Assume from now on that
is a real closed field
. Consider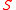
a semi-algebraic system with polynomials in 
. There exist finitely many regular semi-algebraic system
s
such that we have
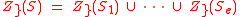where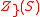 
denotes the points of 
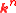which solve 
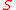. The regular semi-algebraic systems 
form a triangular decomposition of the semi-algebraic system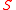 
.
, realized an implementation of this method and reported experimental data in his 1987 pioneer article titled "A zero structure theorem for polynomial equations solving". To put this work into context, let us recall what was the common idea of an algebraic set decomposition at the time this article was written.
Let
be an algebraically closed field
and
be a subfield of 
. A subset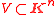 
is an (affine) algebraic variety
over
if there exists a polynomial set 
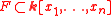such that the zero set 
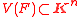of 
equals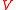 
.
Recall that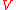
is said irreducible if for all algebraic varieties 
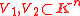the relation 
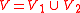implies either 
or 
. A first algebraic variety decomposition result is the famous Lasker–Noether theorem
which implies the following.
The varieties
in the above Theorem are called the irreducible components of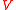 
and can be regarded as a natural output for a decomposition algorithm, or, in other words, for an algorithm solving a system of equations in 
.
In order to lead to a computer program, this algorithm specification should prescribe how irreducible components are represented. Such an encoding is introduced by Joseph Ritt
through the following result.
We call the set
in Ritt's Theorem a Ritt characteristic set of the ideal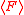 
. Please refer to regular chain
for the notion of a triangular set.
Joseph Ritt
described a method for solving polynomial systems based on polynomial factorization over field extensions and computation of characteristic sets of prime ideals.
Deriving a practical implementation of this method, however, was and remains a difficult problem. In the 80's, when the Characteristic set
Method was introduced, polynomial factorization was an active research area and certain fundamental questions on this subject were solved recently
Nowadays, decomposing an algebraic variety into irreducible components is not essential to process most application problems, since weaker notions of decompositions, less costly to compute, are sufficient.
The Characteristic Set Method relies on the following variant of Ritt's Theorem.
Different concepts and algorithms extended the work of Wen-Tsun Wu
. In the early 90's, the notion of a regular chain
, introduced independently by Michael Kalkbrener in 1991 in his PhD Thesis and, by Lu Yang and Jingzhong Zhang led to important algorithmic discoveries.
In Kalkbrener's vision, regular chains are used to represent the generic zeros of the irreducible components of an algebraic variety. In the original work of Yang and Zhang, they are used to decide whether a hypersurface intersects a quasi-variety (given by a regular chain). Regular chain
s have, in fact, several interesting properties and are the key notion in many algorithms for decomposing systems of algebraic or differential equations.
Regular chains have been investigated in many papers, among them are.
The abundant literature on the subject can be explained by the many equivalent definitions of a regular chain. Actually, the original formulation of Kalkbrener is quite different from that Yang and Zhang. A bridge between these two notions the point of view of Kalkbrener and that of Yang and Zhang appears in Dongming Wang's paper.
There are various algorithms available for obtaining triangular decomposition of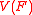
in the sense of Kalkbrener and in the sense of Lazard and Wen-Tsun Wu
. The Lextriangular Algorithm by Daniel Lazard and the Triade Algorithm by Marc Moreno Maza together with the Characteristic Set Method are available in various computer algebra systems, including Maple
and Axiom (computer algebra system).
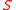is a set of simpler polynomial systems such that a point is a solution of 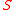if and only if it is a solution of one of the systems .When the purpose is to describe the solution set of
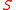in the algebraic closureAlgebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of its coefficient field, those simpler systems are regular chain
Regular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
s. If the coefficient of
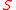are real numbers, then the real solutions of 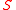can be obtained by a triangular decomposition into regular semi-algebraic systemRegular semi-algebraic system
In computer algebra, a regular semi-algebraic system is a particular kind of triangular system of multivariate polynomials over a real closed field.- Introduction :...
s. In both cases, each of these simpler systems has a triangular shape and remarkable properties, which justifies the terminology.
Formal definitions
Let be a field and be ordered variables. We denote by 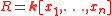the corresponding polynomial ring. Let be a subset of . There are two notions of a triangular decomposition of (regarded as a system of polynomial equations) over the algebraic closureAlgebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of
. The first one is to decompose lazily, by representing only the generic pointGeneric point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
s of the algebraic set
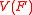in the so-called sense of Kalkbrener.
-
.
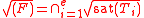The second is to describe explicitly all the points of
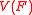in the so-called sense of in Lazard and Wen-Tsun WuWu Wenjun
Wu Wenjun is a Chinese mathematician and academician at the Chinese Academy of Sciences .-Biography:Wu's ancestral hometown is Jiashan, in Jiaxing of Zhejiang. Wu was born in Shanghai, China where he would later graduate from Chiao Tung University in 1940...
.
-
.
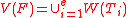In both cases
are finitely many regular chainRegular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
s of
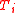and denotes the radical of the saturated ideal of while 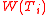denotes the quasi-component of 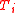. Please refer to regular chainRegular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
for definitions of these notions.
Assume from now on that
is a real closed fieldReal closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
. Consider
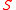a semi-algebraic system with polynomials in . There exist finitely many regular semi-algebraic systemRegular semi-algebraic system
In computer algebra, a regular semi-algebraic system is a particular kind of triangular system of multivariate polynomials over a real closed field.- Introduction :...
s
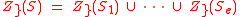such that we have where 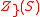denotes the points of 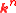which solve 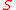. The regular semi-algebraic systems form a triangular decomposition of the semi-algebraic system 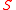.History
The Characteristic Set Method is the first factorization-free algorithm which was proposed for decomposing an algebraic variety into equidimensional components. Moreover, the Author, Wen-Tsun WuWu Wenjun
Wu Wenjun is a Chinese mathematician and academician at the Chinese Academy of Sciences .-Biography:Wu's ancestral hometown is Jiashan, in Jiaxing of Zhejiang. Wu was born in Shanghai, China where he would later graduate from Chiao Tung University in 1940...
, realized an implementation of this method and reported experimental data in his 1987 pioneer article titled "A zero structure theorem for polynomial equations solving". To put this work into context, let us recall what was the common idea of an algebraic set decomposition at the time this article was written.
Let
be an algebraically closed fieldAlgebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
and
be a subfield of . A subset 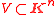is an (affine) algebraic varietyAlgebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
over
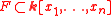if there exists a polynomial set such that the zero set 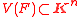of equals 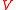.Recall that
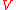is said irreducible if for all algebraic varieties 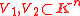the relation 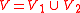implies either or . A first algebraic variety decomposition result is the famous Lasker–Noether theoremLasker–Noether theorem
In mathematics, the Lasker–Noether theorem states that every Noetherian ring is a Lasker ring, which means that every ideal can be written as an intersection of finitely many primary ideals...
which implies the following.
- Theorem (Lasker - Noether)
- For each algebraic variety
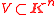there exist finitely many irreducible algebraic varieties 
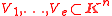such that we have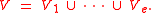
- Moreover, if
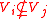holds for 
then the set 
is unique and forms the irreducible decomposition of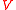 
.
The varieties
in the above Theorem are called the irreducible components of 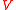and can be regarded as a natural output for a decomposition algorithm, or, in other words, for an algorithm solving a system of equations in .In order to lead to a computer program, this algorithm specification should prescribe how irreducible components are represented. Such an encoding is introduced by Joseph Ritt
Joseph Ritt
Joseph Fels Ritt was an American mathematician at Columbia University in the early 20th century.After beginning his undergraduate studies at City College of New York, Ritt received his B.A. from George Washington University in 1913. He then earned a doctorate in mathematics from Columbia...
through the following result.
- Theorem (Ritt).
- If
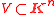is a non-empty and irreducible variety then one can compute a reduced triangular set 
contained in the ideal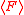 
generated by 
in 
and such that all polynomial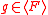 
reduces to zero by pseudo-division w.r.t 
.
We call the set
in Ritt's Theorem a Ritt characteristic set of the ideal 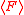. Please refer to regular chainRegular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
for the notion of a triangular set.
Joseph Ritt
Joseph Ritt
Joseph Fels Ritt was an American mathematician at Columbia University in the early 20th century.After beginning his undergraduate studies at City College of New York, Ritt received his B.A. from George Washington University in 1913. He then earned a doctorate in mathematics from Columbia...
described a method for solving polynomial systems based on polynomial factorization over field extensions and computation of characteristic sets of prime ideals.
Deriving a practical implementation of this method, however, was and remains a difficult problem. In the 80's, when the Characteristic set
Characteristic set
Wenjun Wu's method is an algorithm for solving multivariate polynomial equations introduced in the late 1970s by the Chinese mathematician Wen-Tsun Wu. This method is based on the mathematical concept of characteristic set introduced in the late 1940s by J.F. Ritt...
Method was introduced, polynomial factorization was an active research area and certain fundamental questions on this subject were solved recently
Nowadays, decomposing an algebraic variety into irreducible components is not essential to process most application problems, since weaker notions of decompositions, less costly to compute, are sufficient.
The Characteristic Set Method relies on the following variant of Ritt's Theorem.
- Theorem (Wen-Tsun Wu)
- For any finite polynomial set
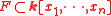, one can compute a reduced triangular set 
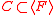such that all polynomial 
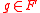reduces to zero by pseudo-division w.r.t 
.
Different concepts and algorithms extended the work of Wen-Tsun Wu
Wu Wenjun
Wu Wenjun is a Chinese mathematician and academician at the Chinese Academy of Sciences .-Biography:Wu's ancestral hometown is Jiashan, in Jiaxing of Zhejiang. Wu was born in Shanghai, China where he would later graduate from Chiao Tung University in 1940...
. In the early 90's, the notion of a regular chain
Regular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
, introduced independently by Michael Kalkbrener in 1991 in his PhD Thesis and, by Lu Yang and Jingzhong Zhang led to important algorithmic discoveries.
In Kalkbrener's vision, regular chains are used to represent the generic zeros of the irreducible components of an algebraic variety. In the original work of Yang and Zhang, they are used to decide whether a hypersurface intersects a quasi-variety (given by a regular chain). Regular chain
Regular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
s have, in fact, several interesting properties and are the key notion in many algorithms for decomposing systems of algebraic or differential equations.
Regular chains have been investigated in many papers, among them are.
The abundant literature on the subject can be explained by the many equivalent definitions of a regular chain. Actually, the original formulation of Kalkbrener is quite different from that Yang and Zhang. A bridge between these two notions the point of view of Kalkbrener and that of Yang and Zhang appears in Dongming Wang's paper.
There are various algorithms available for obtaining triangular decomposition of
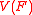in the sense of Kalkbrener and in the sense of Lazard and Wen-Tsun WuWu Wenjun
Wu Wenjun is a Chinese mathematician and academician at the Chinese Academy of Sciences .-Biography:Wu's ancestral hometown is Jiashan, in Jiaxing of Zhejiang. Wu was born in Shanghai, China where he would later graduate from Chiao Tung University in 1940...
. The Lextriangular Algorithm by Daniel Lazard and the Triade Algorithm by Marc Moreno Maza together with the Characteristic Set Method are available in various computer algebra systems, including Maple
Maple (software)
Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....
and Axiom (computer algebra system).
See also
- Characteristic setCharacteristic setWenjun Wu's method is an algorithm for solving multivariate polynomial equations introduced in the late 1970s by the Chinese mathematician Wen-Tsun Wu. This method is based on the mathematical concept of characteristic set introduced in the late 1940s by J.F. Ritt...
- Regular chainRegular chainIn computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
- RegularChainsRegularChainsThe RegularChains package in the computer algebra software package Maple is a collection of commands for solving systems of polynomial equations, inequations and inequalities symbolically....
- Regular semi-algebraic systemRegular semi-algebraic systemIn computer algebra, a regular semi-algebraic system is a particular kind of triangular system of multivariate polynomials over a real closed field.- Introduction :...