Lasker–Noether theorem
Encyclopedia
In mathematics
, the Lasker–Noether theorem states that every Noetherian ring
is a Lasker ring, which means that every ideal can be written as an intersection of finitely many primary ideal
s (which are related to, but not quite the same as, powers of prime ideal
s). The theorem was first proven by for the special case of polynomial ring
s and convergent power series rings, and was proven in its full generality by .
The Lasker–Noether theorem is an extension of the fundamental theorem of arithmetic
, and more generally the fundamental theorem of finitely generated abelian groups to all Noetherian rings.
It has a straightforward extension to modules stating that every submodule of a finitely generated module over a Noetherian ring is a finite intersection of primary submodules. This contains the case for rings as a special case, considering the ring as a module over itself, so that ideals are submodules. This also generalizes the primary decomposition form of the structure theorem for finitely generated modules over a principal ideal domain
, and for the special case of polynomial rings over a field, it generalizes the decomposition of an algebraic set into a finite union of (irreducible) varieties.
The first algorithm for computing primary decompositions for polynomial rings was published by Noether's student .
An equivalent statement is: every finitely generated module over a Noetherian ring is contained in a finite product of coprimary modules.
The Lasker–Noether theorem follows immediately from the following three facts:
,
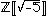in which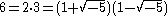
.
If a number does not factor uniquely into primes, then the ideal generated by the number may still factor into the intersection of powers of prime ideals. Failing that, an ideal may at least factor into the intersection of primary ideals.
Let R be a Noetherian ring, and I an ideal in R. Then I has an irredundant primary decomposition into primary ideals.
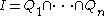
Irredundancy means:
for all i, where the hat denotes omission.
More over, this decomposition is unique in the following sense: the set of associated prime ideals is unique, and the primary ideal above every minimal prime in this set is also unique. However, primary ideals which are associated with non-minimal prime ideals are in general not unique.
In the case of the ring of integers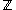
, the Lasker–Noether theorem is equivalent to the fundamental theorem of arithmetic
. If an integer n has prime factorization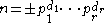
, then the primary decomposition of the ideal generated by 
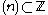, is
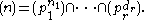
A primary decomposition of a submodule M of a module N is called minimal if it has the smallest possible number of primary modules. For minimal decompositions, the primes of the primary modules are uniquely determined: they are the associated primes of N/M. Moreover the primary submodules associated to the minimal or isolated associated primes (those not containing any other associated primes) are also unique. However the primary submodules associated to the non-minimal associated primes (called embedded primes for geometric reasons) need not be unique.
Example: Let N = R = k[x, y] for some field k, and let M be the ideal (xy, y2). Then M has two different minimal primary decompositions
M = (y) ∩ (x, y2) = (y) ∩ (x + y, y2).
The minimal prime is (y) and the embedded prime is (x, y).
s is a useful substitute for the class of primary ideals.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lasker–Noether theorem states that every Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
is a Lasker ring, which means that every ideal can be written as an intersection of finitely many primary ideal
Primary ideal
In mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
s (which are related to, but not quite the same as, powers of prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s). The theorem was first proven by for the special case of polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
s and convergent power series rings, and was proven in its full generality by .
The Lasker–Noether theorem is an extension of the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
, and more generally the fundamental theorem of finitely generated abelian groups to all Noetherian rings.
It has a straightforward extension to modules stating that every submodule of a finitely generated module over a Noetherian ring is a finite intersection of primary submodules. This contains the case for rings as a special case, considering the ring as a module over itself, so that ideals are submodules. This also generalizes the primary decomposition form of the structure theorem for finitely generated modules over a principal ideal domain
Structure theorem for finitely generated modules over a principal ideal domain
In mathematics, in the field of abstract algebra, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in...
, and for the special case of polynomial rings over a field, it generalizes the decomposition of an algebraic set into a finite union of (irreducible) varieties.
The first algorithm for computing primary decompositions for polynomial rings was published by Noether's student .
Definitions
Write R for a commutative ring, and M and N for modules over it.- A zero divisor of a module M is an element x of R such that xm = 0 for some non-zero m in M.
- An element x of R is called nilpotent in M if xnM = 0 for some positive integer n.
- A module is called coprimary if every zero divisor of M is nilpotent in M. For example, groups of prime power order and free abelian groups are coprimary modules over the ring of integers.
- A submodule M of a module N is called a primary submodule if N/M is coprimary.
- An ideal I is called primaryPrimary idealIn mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
if it is a primary submodule of R. This is equivalent to saying that if ab is in I then either a is in I or bn is in I for some n, and to the condition that every zero-divisor of the ring R/I is nilpotent. - A submodule M of a module N is called irreducible if it is not an intersection of two strictly larger submodules.
- An associated prime of a module M is a prime ideal that is the annihilator of some element of M.
Statement
The Lasker–Noether theorem for modules states every submodule of a finitely generated module over a Noetherian ring is a finite intersection of primary submodules. For the special case of ideals it states that every ideal of a Noetherian ring is a finite intersection of primary ideals.An equivalent statement is: every finitely generated module over a Noetherian ring is contained in a finite product of coprimary modules.
The Lasker–Noether theorem follows immediately from the following three facts:
- Any submodule of a finitely generated module over a Noetherian ring is an intersection of a finite number of irreducible submodules.
- If M is an irreducible submodule of a finitely generated module N over a Noetherian ring then N/M has only one associated prime ideal.
- A finitely generated module over a Noetherian ring is coprimary if and only if it has at most one associated prime.
Irreducible decomposition in rings
The study of the decomposition of ideals in rings began as a remedy for the lack of unique factorization in number fields like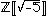,in which
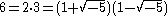.If a number does not factor uniquely into primes, then the ideal generated by the number may still factor into the intersection of powers of prime ideals. Failing that, an ideal may at least factor into the intersection of primary ideals.
Let R be a Noetherian ring, and I an ideal in R. Then I has an irredundant primary decomposition into primary ideals.
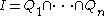
Irredundancy means:
- Removing any of the
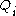changes the intersection, i.e.,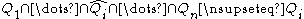
for all i, where the hat denotes omission.
- The associated prime ideals
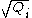are distinct.
More over, this decomposition is unique in the following sense: the set of associated prime ideals is unique, and the primary ideal above every minimal prime in this set is also unique. However, primary ideals which are associated with non-minimal prime ideals are in general not unique.
In the case of the ring of integers
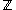, the Lasker–Noether theorem is equivalent to the fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
. If an integer n has prime factorization
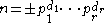, then the primary decomposition of the ideal generated by 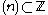, is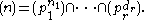Minimal decompositions and uniqueness
In this section, all modules will be finitely generated over a Noetherian ring R.A primary decomposition of a submodule M of a module N is called minimal if it has the smallest possible number of primary modules. For minimal decompositions, the primes of the primary modules are uniquely determined: they are the associated primes of N/M. Moreover the primary submodules associated to the minimal or isolated associated primes (those not containing any other associated primes) are also unique. However the primary submodules associated to the non-minimal associated primes (called embedded primes for geometric reasons) need not be unique.
Example: Let N = R = k[x, y] for some field k, and let M be the ideal (xy, y2). Then M has two different minimal primary decompositions
M = (y) ∩ (x, y2) = (y) ∩ (x + y, y2).
The minimal prime is (y) and the embedded prime is (x, y).
When the conclusion does not hold
The decomposition does not hold in general for non-commutative Noetherian rings. Noether gave an example of a non-commutative Noetherian ring with a right ideal that is not an intersection of primary ideals.Additive theory of ideals
This result is the first in an area now known as the additive theory of ideals, which studies the ways of representing an ideal as the intersection of a special class of ideals. The decision on the "special class", e.g., primary ideals, is a problem in itself. In the case of non-commutative rings, the class of tertiary idealTertiary ideal
In mathematics, a tertiary ideal is an ideal in a ring that cannot be expressed as a nontrivial intersection of a right fractional ideal with another ideal. Tertiary ideals generalize primary ideals to the case of noncommutative rings...
s is a useful substitute for the class of primary ideals.