Associated prime
Encyclopedia
In abstract algebra
, an associated prime of a module
M over a ring
R is a type of prime ideal
of R that arises as an annihilator
of a submodule of M. The set of associated primes is usually denoted by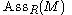
.
In commutative algebra
, associated primes are linked to the Lasker-Noether primary decomposition
of ideals in commutative Noetherian ring
s. Specifically, if an ideal J is decomposed as a finite intersection of primary ideal
s, it is known that the radicals
of these primary ideals are prime ideal
s, and this set of prime ideals coincides with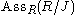
. Also linked with the concept of "associated primes" of the ideal are the notions of isolated primes and embedded primes.
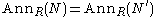for any nonzero submodule N' of N. For a prime module N, 
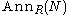is a prime ideal in R.
An associated prime of an R module M is an ideal of the form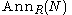
where N is a prime submodule of M. In commutative algebra the usual definition is different, but equivalent: if R is commutative, an associated prime of M is a prime ideal which is of the form 
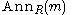for a nonzero element m of M.
In a commutative ring R, an associated prime of M is called an isolated prime if it does not properly contain another associated prime of M. An associated prime properly containing another associated prime is called an embedded prime.
A module is called coprimary if xm = 0 for some nonzero m ∈ M implies xnM = 0 for some positive integer n. A finitely generated module over a commutative Noetherian ring
is coprimary if and only if it has at most one associated prime.
The following properties all refer to a commutative Noetherian ring R:
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, an associated prime of a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
M over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R is a type of prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
of R that arises as an annihilator
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
of a submodule of M. The set of associated primes is usually denoted by
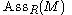.In commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, associated primes are linked to the Lasker-Noether primary decomposition
Lasker–Noether theorem
In mathematics, the Lasker–Noether theorem states that every Noetherian ring is a Lasker ring, which means that every ideal can be written as an intersection of finitely many primary ideals...
of ideals in commutative Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
s. Specifically, if an ideal J is decomposed as a finite intersection of primary ideal
Primary ideal
In mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
s, it is known that the radicals
Radical of an ideal
In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
of these primary ideals are prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s, and this set of prime ideals coincides with
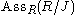. Also linked with the concept of "associated primes" of the ideal are the notions of isolated primes and embedded primes.Definitions
A nonzero R module N is called a prime module if the annihilator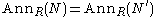 for any nonzero submodule N' of N. For a prime module N, 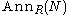is a prime ideal in R.An associated prime of an R module M is an ideal of the form
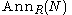where N is a prime submodule of M. In commutative algebra the usual definition is different, but equivalent: if R is commutative, an associated prime of M is a prime ideal which is of the form 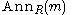for a nonzero element m of M.In a commutative ring R, an associated prime of M is called an isolated prime if it does not properly contain another associated prime of M. An associated prime properly containing another associated prime is called an embedded prime.
A module is called coprimary if xm = 0 for some nonzero m ∈ M implies xnM = 0 for some positive integer n. A finitely generated module over a commutative Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
is coprimary if and only if it has at most one associated prime.
Properties
Most of these properties and assertions are given in starting on page 86.- If M' ⊆M, then
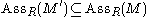. If in addition M' is an essential submodule of M, their associated primes coincide. - It is possible, even for a commutative local ring, that the set of associated primes of a finitely generated module is empty. However, in any ring satisfying the ascending chain conditionAscending chain conditionThe ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
on ideals (for example, any right or left Noetherian ring) every nonzero module has at least one associated prime. - Any uniform moduleUniform moduleIn abstract algebra, a module is called a uniform module if the intersection of any two nonzero submodules is nonzero. This is equivalent to saying that every nonzero submodule of M is an essential submodule...
has either zero or one associated primes, making uniform modules an example of coprimary modules. - For a one-sided Noetherian ring, there is a surjection from the set of isomorphism classes of indecomposable injective moduleInjective moduleIn mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
s onto the spectrumSpectrum of a ringIn abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
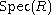. If R is an Artinian ringArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
, then this map becomes a bijection. - Matlis' Theorem: For a commutative Noetherian ring R, the map from the isomorphism classes of indecomposable injective modules to the spectrum is a bijection. Moreover, a complete set of representatives for those classes is given by
where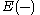 
denotes the injective hullInjective hullIn mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...
and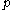
ranges over the prime ideals of R. - For a Noetherian moduleNoetherian moduleIn abstract algebra, an Noetherian module is a module that satisfies the ascending chain condition on its submodules, where the submodules are partially ordered by inclusion....
M over any ring, there are only finitely many associated primes of M.
The following properties all refer to a commutative Noetherian ring R:
- An ideal J is a primary idealPrimary idealIn mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
if and only if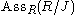
has exactly one element. - Every ideal J (through primary decomposition) is expressible as a finite intersection of primary ideals. The radical of each of these ideals is a prime ideal, and these primes are exactly the elements of
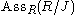. - Any prime ideal minimal with respect to containing an ideal J is in
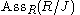. These primes are precisely the isolated primes. - The set theoretic union of the associated primes of M is exactly the collection of zero-divisors on M, that is, elements r for which there exists nonzero m in M with mr =0.
- If M is a finitely generated module over R, then there is a finite ascending sequence of submodules
-
-
- such that each quotient Mi/Mi−1 is isomorphic to R/Pi for some prime ideals Pi. Moreover every associated prime of M occurs among the set of primes Pi. (In general not all the ideals Pi are associated primes of M.)
Examples
- If R is the ring of integers, then non-trivial free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
s and non-trivial abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s of prime power order are coprimary. - If R is the ring of integers and M a finite abelian group, then the associated primes of M are exactly the primes dividing the order of M.
- The group of order 2 is a quotient of the integers Z (considered as a free module over itself), but its associated prime ideal (2) is not an associated prime of Z.