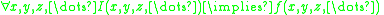Characteristic set
Encyclopedia
Wenjun Wu
's method is an algorithm for solving multivariate polynomial equations
introduced in the late 1970s by the Chinese mathematician Wen-Tsun Wu
. This method is based on the mathematical concept of characteristic set introduced in the late 1940s by J.F. Ritt
. It is fully independent of Gröbner basis
method, introduced by Bruno Buchberger
(1965), even if Gröbner bases may be used to compute characteristic sets .
Wu's method is powerful for mechanical theorem proving in elementary geometry, and provides a complete decision process for certain classes of problem.
It has been used in research in his laboratory (KLMM, Key Laboratory of Mathematics Mechanization in Chinese Academy of Science) and around the world. The main trends of research on Wu's method concern systems of polynomial equations of positive dimension and differential algebra
where Ritt
's results have been made effective . Wu's method has been applied in various scientific fields, like biology, computer vision, robot kinematics and especially automatic proofs in geometry
division to solve problems of the form:
where f is a polynomial equation and I is a conjunction
of polynomial equations. The algorithm is complete for such problems over the complex domain.
The core idea of the algorithm is that you can divide one polynomial by another to give a remainder. Repeated division results in either the remainder vanishing (in which case the I implies f statement is true), or an irreducible remainder is left behind (in which case the statement is false).
More specifically, for an ideal
I in the ring
k[x1, ..., xn] over a field k, a (Ritt) characteristic set C of I is composed of a set of polynomials in I, which is in triangular shape: polynomials in C have distinct main variables (see the formal definition below). Given a characteristic set C of I, one can decide if a polynomial f is zero modulo I. That is, the membership test is checkable for I, provided a characteristic set of I.
certain minimal condition with respect to the Ritt ordering, and it preserves many interesting geometrical properties
of the ideal. However it may not be its system of generators.
Let R be the multivariate polynomial ring k[x1, ..., xn] over a field k.
The variables are ordered linearly according to their subscript: x1 < ... < xn.
For a non-constant polynomial p in R, the greatest variable effectively presenting in p, called main variable or class, plays a particular role:
p can be naturally regarded as a univariate polynomial in its main variable xk with coefficients in k[x1, ..., xk−1].
The degree of p as a univariate polynomial in its main variable is also called its main degree.
A set T of non-constant polynomials is called a triangular set if all polynomials in T have dinstinct main variables. This generalizes triangular systems of linear equations in a natural way.
For two non-constant polynomials p and q, we say p is smaller than q with respect to Ritt ordering and written as p <r q, if one of the following assertions holds: the main variable of p is smaller than the main variable of q, that is, mvar(p) < mvar(q), p and q have the same main variable, and the main degree of p is less than the main degree of q, that is, mvar(p) = mvar(q) and mdeg(p) < mdeg(q).
In this way, (k[x1, ..., xn],<r) forms a well partial order. However, the Ritt ordering is not a total order
:
there exist polynomials p and q such that neither p <r q nor p r q. In this case, we say that p and q are not comparable.
Note that the Ritt ordering is comparing the rank of p and q. The rank, denotey by rank(p), of a non-constant polynomial p is defined to be a power of
its main variable: mvar(p)mdeg(p) and ranks are compared by comparing first the variables and then, in case of equality of the variables, the degrees.
A crucial generalization on Ritt ordering is to compare triangular sets.
Let T = { t1, ..., tu} and S = { s1, ..., sv} be two triangular sets
such that polynomials in T and S are sorted increasingly according to their main variables.
We say T is smaller than U w.r.t. Ritt ordering if one of the following assertions holds there exists k ≤ min(u, v) such that rank(ti) = rank(si) for 1 ≤ i < k and tk <r sk, u > v and rank(ti) = rank(si) for 1 ≤ i ≤ v.
Also, there exists incomparable triangular sets w.r.t Ritt ordering.
Let I be a non-zero ideal of k[x1, ..., xn]. A subset T of I is a Ritt characteristic set of I if one of the following conditions holds: T consists of a single nonzero constant of k, T is a triangular set and T is minimal w.r.t Ritt ordering in the set of all fine triangular sets contained in I.
A polynomial ideal may possess (infinitely) many characteristic sets, since Ritt ordering is a partial order.
A non-empty subset T of the ideal generated by F is a Wu characteristic set of F if one of the following condition holds
T = {a} with a being a nonzero constant, T is a triangular set and there exists a subset G of such that = and every polynomial in G is pseudo-reduced
to zero with respect to T.
Note that Wu characteristic set is defined to the set F of polynomials, rather to the ideal generated by F. Also it can be shown that a Ritt characteristic set T of is a Wu characteristic set of F. Wu characteristic sets can be computed by Wu's algorithm CHRST-REM, which only requires pseudo-remainder computations and no factorizations are needed.
Wu's characteristic set method has exponential complexity; improvements in computing efficiency by weak chains, regular chain
s, saturated chain were introduced
Te such that:
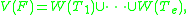
where W(Ti) is the difference of V(Ti) and V(hi), here hi is the product of initials of the polynomials in Ti.
Wu Wenjun
Wu Wenjun is a Chinese mathematician and academician at the Chinese Academy of Sciences .-Biography:Wu's ancestral hometown is Jiashan, in Jiaxing of Zhejiang. Wu was born in Shanghai, China where he would later graduate from Chiao Tung University in 1940...
's method is an algorithm for solving multivariate polynomial equations
Systems of polynomial equations
A system of polynomial equations is a set of simultaneous equations f1 = 0, ..., fh = 0 where the fi are polynomials in several variables, say x1, ..., xn, over some field k....
introduced in the late 1970s by the Chinese mathematician Wen-Tsun Wu
Wu Wenjun
Wu Wenjun is a Chinese mathematician and academician at the Chinese Academy of Sciences .-Biography:Wu's ancestral hometown is Jiashan, in Jiaxing of Zhejiang. Wu was born in Shanghai, China where he would later graduate from Chiao Tung University in 1940...
. This method is based on the mathematical concept of characteristic set introduced in the late 1940s by J.F. Ritt
Joseph Ritt
Joseph Fels Ritt was an American mathematician at Columbia University in the early 20th century.After beginning his undergraduate studies at City College of New York, Ritt received his B.A. from George Washington University in 1913. He then earned a doctorate in mathematics from Columbia...
. It is fully independent of Gröbner basis
Gröbner basis
In computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
method, introduced by Bruno Buchberger
Bruno Buchberger
Bruno Buchberger is Professor of Computer Mathematics at Johannes Kepler University in Linz, Austria. In his 1965 Ph.D. thesis, he created the theory of Gröbner bases, and has developed this theory throughout his career. He named these objects after his advisor Wolfgang Gröbner...
(1965), even if Gröbner bases may be used to compute characteristic sets .
Wu's method is powerful for mechanical theorem proving in elementary geometry, and provides a complete decision process for certain classes of problem.
It has been used in research in his laboratory (KLMM, Key Laboratory of Mathematics Mechanization in Chinese Academy of Science) and around the world. The main trends of research on Wu's method concern systems of polynomial equations of positive dimension and differential algebra
Differential algebra
In mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
where Ritt
Joseph Ritt
Joseph Fels Ritt was an American mathematician at Columbia University in the early 20th century.After beginning his undergraduate studies at City College of New York, Ritt received his B.A. from George Washington University in 1913. He then earned a doctorate in mathematics from Columbia...
's results have been made effective . Wu's method has been applied in various scientific fields, like biology, computer vision, robot kinematics and especially automatic proofs in geometry
Informal description
Wu's method uses polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
division to solve problems of the form:
where f is a polynomial equation and I is a conjunction
Conjunction
Conjunction can refer to:* Conjunction , an astronomical phenomenon* Astrological aspect, an aspect in horoscopic astrology* Conjunction , a part of speech** Conjunctive mood , same as subjunctive mood...
of polynomial equations. The algorithm is complete for such problems over the complex domain.
The core idea of the algorithm is that you can divide one polynomial by another to give a remainder. Repeated division results in either the remainder vanishing (in which case the I implies f statement is true), or an irreducible remainder is left behind (in which case the statement is false).
More specifically, for an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
I in the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
k[x1, ..., xn] over a field k, a (Ritt) characteristic set C of I is composed of a set of polynomials in I, which is in triangular shape: polynomials in C have distinct main variables (see the formal definition below). Given a characteristic set C of I, one can decide if a polynomial f is zero modulo I. That is, the membership test is checkable for I, provided a characteristic set of I.
Ritt characteristic set
A Ritt characteristic set is a finite set of polynomials in triangular form of an ideal. This triangular set satisfiescertain minimal condition with respect to the Ritt ordering, and it preserves many interesting geometrical properties
of the ideal. However it may not be its system of generators.
- Notation
Let R be the multivariate polynomial ring k[x1, ..., xn] over a field k.
The variables are ordered linearly according to their subscript: x1 < ... < xn.
For a non-constant polynomial p in R, the greatest variable effectively presenting in p, called main variable or class, plays a particular role:
p can be naturally regarded as a univariate polynomial in its main variable xk with coefficients in k[x1, ..., xk−1].
The degree of p as a univariate polynomial in its main variable is also called its main degree.
- Triangular set
A set T of non-constant polynomials is called a triangular set if all polynomials in T have dinstinct main variables. This generalizes triangular systems of linear equations in a natural way.
- Ritt ordering
For two non-constant polynomials p and q, we say p is smaller than q with respect to Ritt ordering and written as p <r q, if one of the following assertions holds: the main variable of p is smaller than the main variable of q, that is, mvar(p) < mvar(q), p and q have the same main variable, and the main degree of p is less than the main degree of q, that is, mvar(p) = mvar(q) and mdeg(p) < mdeg(q).
In this way, (k[x1, ..., xn],<r) forms a well partial order. However, the Ritt ordering is not a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
:
there exist polynomials p and q such that neither p <r q nor p r q. In this case, we say that p and q are not comparable.
Note that the Ritt ordering is comparing the rank of p and q. The rank, denotey by rank(p), of a non-constant polynomial p is defined to be a power of
its main variable: mvar(p)mdeg(p) and ranks are compared by comparing first the variables and then, in case of equality of the variables, the degrees.
- Ritt ordering on triangular sets
A crucial generalization on Ritt ordering is to compare triangular sets.
Let T = { t1, ..., tu} and S = { s1, ..., sv} be two triangular sets
such that polynomials in T and S are sorted increasingly according to their main variables.
We say T is smaller than U w.r.t. Ritt ordering if one of the following assertions holds there exists k ≤ min(u, v) such that rank(ti) = rank(si) for 1 ≤ i < k and tk <r sk, u > v and rank(ti) = rank(si) for 1 ≤ i ≤ v.
Also, there exists incomparable triangular sets w.r.t Ritt ordering.
- Ritt characteristic set
Let I be a non-zero ideal of k[x1, ..., xn]. A subset T of I is a Ritt characteristic set of I if one of the following conditions holds: T consists of a single nonzero constant of k, T is a triangular set and T is minimal w.r.t Ritt ordering in the set of all fine triangular sets contained in I.
A polynomial ideal may possess (infinitely) many characteristic sets, since Ritt ordering is a partial order.
Wu characteristic set
The Ritt–Wu process, first devised by Ritt, subsequently modified by Wu, computes not a Ritt characteristic but an extended one, called Wu characteristic set or ascending chain.A non-empty subset T of the ideal
T = {a} with a being a nonzero constant, T is a triangular set and there exists a subset G of
Regular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
to zero with respect to T.
Note that Wu characteristic set is defined to the set F of polynomials, rather to the ideal
Wu's characteristic set method has exponential complexity; improvements in computing efficiency by weak chains, regular chain
Regular chain
In computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
s, saturated chain were introduced
Decomposing algebraic varieties
An application is an algorithm for solving systems of algebraic equations by means of characteristic sets. More precisely, given a finite subset F of polynomials, there is an algorithm to compute characteristic sets T1, ...,Te such that:
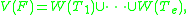
where W(Ti) is the difference of V(Ti) and V(hi), here hi is the product of initials of the polynomials in Ti.
See also
- Groebner basis
- Regular chainRegular chainIn computer algebra, a regular chain is a particular kind of triangular set in a multivariate polynomial ring over a field. It enhances the notion of characteristic set.- Introduction :...
- Mathematics-Mechanization Platform
- RegularChainsRegularChainsThe RegularChains package in the computer algebra software package Maple is a collection of commands for solving systems of polynomial equations, inequations and inequalities symbolically....