Presheaf (category theory)
Encyclopedia
In category theory
, a branch of mathematics
, a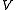
-valued presheaf 
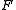on a category 
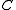is a functor
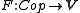. Often presheaf is defined to be a Set-valued presheaf. If 
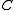is the poset of open set
s in a topological space
, interpreted as a category, then one recovers the usual notion of presheaf on a topological space.
A morphism of presheaves is defined to be a natural transformation
of functors. This makes the collection of all presheaves into a category, often written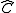
. A functor into 
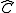is sometimes called a profunctor
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a
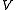-valued presheaf 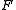on a category 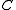is a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
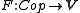. Often presheaf is defined to be a Set-valued presheaf. If is the poset of open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s in a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, interpreted as a category, then one recovers the usual notion of presheaf on a topological space.
A morphism of presheaves is defined to be a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
of functors. This makes the collection of all presheaves into a category, often written
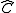. A functor into 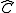is sometimes called a profunctorProfunctor
In category theory, a branch of mathematics, profunctors are a generalization of relations and also of bimodules. They are related to the notion of correspondences.- Definition :...
.
Properties
- A locally small category
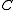embeds fully and faithfully into the category 
of set-valued presheaves via the Yoneda embedding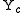 
which to every object 
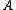of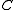 
associates the hom-set 
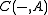. - The presheaf category
is (up to equivalence of categories) the free colimit completion of the category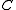 
.