
Godement resolution
Encyclopedia
The Godement resolution of a sheaf
is a construction in homological algebra
which allows one to view global, cohomological information about the sheaf in terms of local information coming from its stalks. It is useful for computing sheaf cohomology
. It was discovered by Roger Godement
.
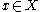 , let
, let 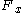 denote the stalk of F at x. Given an open set
denote the stalk of F at x. Given an open set 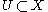 , define
, define
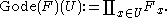
An open subset clearly induces a restriction map
clearly induces a restriction map  , so Gode(F) is a presheaf. One checks the sheaf
, so Gode(F) is a presheaf. One checks the sheaf
axiom easily. One also proves easily that Gode(F) is flabby, meaning each restriction map is surjective. Gode can be turned into a functor because a map between two sheaves induces maps between their stalks. Finally, there is a canonical map of sheaves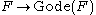 which sends each section to the product of its germs. This canonical map is a natural transformation between the identity functor and Gode.
which sends each section to the product of its germs. This canonical map is a natural transformation between the identity functor and Gode.
Another way to view Gode is as follows. Let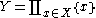 be the disjoint union of the points of X. There is a continuous map . This induces adjoint pushforward and pullback functors p* and p*. Gode is the unit of this adjunction, that is, it is p*p*.
be the disjoint union of the points of X. There is a continuous map . This induces adjoint pushforward and pullback functors p* and p*. Gode is the unit of this adjunction, that is, it is p*p*.
In more down-to-earth terms, let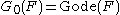 , and let
, and let 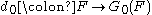 denote the canonical map. For each
denote the canonical map. For each 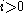 , let
, let 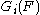 denote
denote 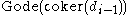 , and let
, and let 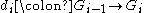 denote the canonical map. The resulting resolution
denote the canonical map. The resulting resolution
is a flabby resolution of F, and its cohomology is the sheaf cohomology
of F.
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
is a construction in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
which allows one to view global, cohomological information about the sheaf in terms of local information coming from its stalks. It is useful for computing sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
. It was discovered by Roger Godement
Roger Godement
Roger Godement is a French mathematician, known for his work in functional analysis, and also his expository books.He started as a student at the École normale supérieure in 1940, where he became a student of Henri Cartan...
.
Godement construction
Given a topological space X (more generally, a topos X with enough points), and a sheaf F on X, the Godement construction for F gives a sheaf Gode(F) constructed as follows. For each point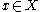 , let
, let 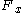 denote the stalk of F at x. Given an open set
denote the stalk of F at x. Given an open set 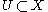 , define
, define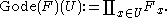
An open subset
 clearly induces a restriction map
clearly induces a restriction map  , so Gode(F) is a presheaf. One checks the sheaf
, so Gode(F) is a presheaf. One checks the sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
axiom easily. One also proves easily that Gode(F) is flabby, meaning each restriction map is surjective. Gode can be turned into a functor because a map between two sheaves induces maps between their stalks. Finally, there is a canonical map of sheaves
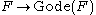 which sends each section to the product of its germs. This canonical map is a natural transformation between the identity functor and Gode.
which sends each section to the product of its germs. This canonical map is a natural transformation between the identity functor and Gode.Another way to view Gode is as follows. Let
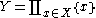 be the disjoint union of the points of X. There is a continuous map . This induces adjoint pushforward and pullback functors p* and p*. Gode is the unit of this adjunction, that is, it is p*p*.
be the disjoint union of the points of X. There is a continuous map . This induces adjoint pushforward and pullback functors p* and p*. Gode is the unit of this adjunction, that is, it is p*p*.Godement resolution
Because Gode is the unit of an adjunction, there is an associated monad on the category of sheaves on X. Using this monad there is a way to turn a sheaf F into a coaugmented cosimplicial sheaf. This coaugmented cosimplicial sheaf is associated to an augmented cochain complex which is defined to be the Godement resolution of F.In more down-to-earth terms, let
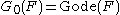 , and let
, and let 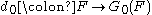 denote the canonical map. For each
denote the canonical map. For each 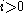 , let
, let 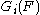 denote
denote 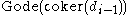 , and let
, and let 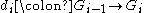 denote the canonical map. The resulting resolution
denote the canonical map. The resulting resolutionResolution (algebra)
In mathematics, particularly in abstract algebra and homological algebra, a resolution is a sequence of objects which is used to describe the structure of a module, or, more generally, the structure of an object in an abelian category.Generally, if the objects involved in the sequence have a...
is a flabby resolution of F, and its cohomology is the sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
of F.

