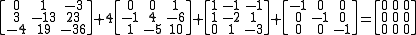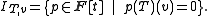Minimal polynomial (linear algebra)
Encyclopedia
In linear algebra
, the minimal polynomial of an n-by-n matrix
A over a field
F is the monic polynomial P over F of least degree such that P(A)=0. Any other polynomial Q with Q(A) = 0 is a (polynomial) multiple of .
The following three statements are equivalent:
The multiplicity of a root λ of is the largest power m such that strictly contains (increasing the exponent up to m will give ever larger kernels, but further increasing m will just give the same kernel).
If the field is not algebraically closed, then the minimal and characteristic polynomials need not factor according to their roots (in ) alone, in other words they may have irreducible polynomial
factors of degree greater than 1. For such factors one has similar equivalences:
Like the characteristic polynomial, the minimal polynomial does not depend on the base field, in other words considering the matrix as one with coefficients in a larger field does not change the minimal polynomial. The reason is somewhat different than for the characteristic polynomial (where it is immediate from the definition of determinants), namely the fact that the minimal polynomial is determined by the relations of linear dependence between the powers of A: extending the base field will not introduce any new such relations (nor of course will it remove existing ones).
The minimal polynomial is often the same as the characteristic polynomial, but not always. For example, if A is a multiple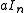
of the identity matrix, then its minimal polynomial is since the kernel of 
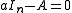is already the entire space; on the other hand its characteristic polynomial is (the only eigenvalue is , and the degree of the characteristic polynomial is always equal to the dimension of the space). The minimal polynomial always divides the characteristic polynomial, which is one way of formulating the Cayley–Hamilton theorem
.
T on a finite-dimensional vector space
V over a field
F, let IT be the set defined as
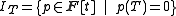
where F[t] is the space of all polynomials over the field F. It is easy to show that IT is a proper ideal
of F[t].
Thus it must be the monic polynomial of least degree in IT.
φ of a finite dimensional vector space over a field F is diagonalizable if and only if its minimal polynomial factors completely over F into distinct linear factors. The fact that there is only one factor for every eigenvalue means that the generalized eigenspace for is the same as the eigenspace for : every Jordan block has size 1. More generally, if φ satisfies a polynomial equation where P factors into distinct linear factors over F, then it will be diagonalizable: its minimal polynomial is a divisor of P and therefore also factors into distinct linear factors. In particular one has:
These case can also be proved directly, but the minimal polynomial gives a unified perspective and proof.
This definition satisfies the properties of a proper ideal. Let μT,v be the monic polynomial which generates it.
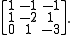
Taking the first canonical basis vector and its repeated images by one obtains
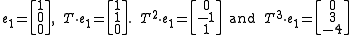
of which the first three are easily seen to be linearly independent, and therefore span all of . The last one then necessarily is a linear combination of the first three, in fact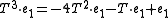
, so that 
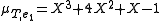. This is in fact also the minimal polynomial 
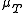and the characteristic polynomial 
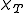: indeed 
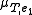divides 
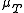which divides 
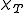, and since the first and last are of degree 3 and all are monic, they must all be the same. Another reason is that in general if any polynomial in annihilates a vector , then it also annihilates (just apply to the equation that says that it annihilates ), and therefore by iteration it annihilates the entire space generated by the iterated images by of ; in the current case we have seen that for that space is all of , so 
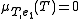. Indeed one verifies for the full matrix that 
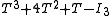is the null matrix: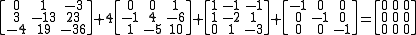
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the minimal polynomial of an n-by-n matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F is the monic polynomial P over F of least degree such that P(A)=0. Any other polynomial Q with Q(A) = 0 is a (polynomial) multiple of .
The following three statements are equivalent:
- λ is a root of ,
- λ is a root of the characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of A, - λ is an eigenvalue of matrix A.
The multiplicity of a root λ of is the largest power m such that strictly contains (increasing the exponent up to m will give ever larger kernels, but further increasing m will just give the same kernel).
If the field is not algebraically closed, then the minimal and characteristic polynomials need not factor according to their roots (in ) alone, in other words they may have irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
factors of degree greater than 1. For such factors one has similar equivalences:
- divides ,
- divides ,
- the kernel of has dimension at least 1.
Like the characteristic polynomial, the minimal polynomial does not depend on the base field, in other words considering the matrix as one with coefficients in a larger field does not change the minimal polynomial. The reason is somewhat different than for the characteristic polynomial (where it is immediate from the definition of determinants), namely the fact that the minimal polynomial is determined by the relations of linear dependence between the powers of A: extending the base field will not introduce any new such relations (nor of course will it remove existing ones).
The minimal polynomial is often the same as the characteristic polynomial, but not always. For example, if A is a multiple
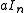of the identity matrix, then its minimal polynomial is since the kernel of 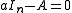is already the entire space; on the other hand its characteristic polynomial is (the only eigenvalue is , and the degree of the characteristic polynomial is always equal to the dimension of the space). The minimal polynomial always divides the characteristic polynomial, which is one way of formulating the Cayley–Hamilton theoremCayley–Hamilton theorem
In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
.
Formal definition
Given an endomorphismEndomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
T on a finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F, let IT be the set defined as
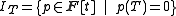
where F[t] is the space of all polynomials over the field F. It is easy to show that IT is a proper ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of F[t].
- The minimal polynomial is the monic polynomial which generates IT.
Thus it must be the monic polynomial of least degree in IT.
Applications
An endomorphismEndomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
φ of a finite dimensional vector space over a field F is diagonalizable if and only if its minimal polynomial factors completely over F into distinct linear factors. The fact that there is only one factor for every eigenvalue means that the generalized eigenspace for is the same as the eigenspace for : every Jordan block has size 1. More generally, if φ satisfies a polynomial equation where P factors into distinct linear factors over F, then it will be diagonalizable: its minimal polynomial is a divisor of P and therefore also factors into distinct linear factors. In particular one has:
-
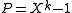: finite order endomorphisms of complex vector spaces are diagonalizable. For the special case of involutions, this is even true for endomorphisms of vector spaces over any field of characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
other than 2, since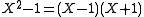
is a factorization into distinct factors over such a field. This is a part of representation theoryRepresentation theoryRepresentation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of cyclic groups. -
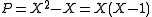: endomorphisms satisfying 
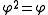are called projectionsProjection (linear algebra)In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
, and are always diagonalizable (moreover their only eigenvalues are 0 and 1). - By contrast if
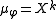with then φ (a nilpotent endomorphism) is not necessarily diagonalizable, since 
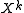has a repeated root 0.
These case can also be proved directly, but the minimal polynomial gives a unified perspective and proof.
Computation
Let IT,v be defined as
This definition satisfies the properties of a proper ideal. Let μT,v be the monic polynomial which generates it.
Properties
- Since IT,v contains minimal polynomial , the latter is divisible by .
- If d is the least latural number such that v, T(v), ... , Td(v) are linearly dependent, then there exist unique
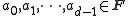such that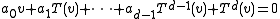
and for these coefficients one has
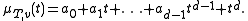
- Let the subspace V be the image of (T), which is T-stable. Since (T) annihilates at least the vectors v, T(v), ... , Td-1(v), the codimensionCodimensionIn mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
of V is at least d. - The minimal polynomial is the product of and the minimal polynomial Q of the restriction of T to V. In the (likely) case that V has dimension 0 one has and therefore ; otherwise a recursive computation of Q suffices to find .
Example
Define to be the endomorphism of with matrix, on the canonical basis,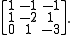Taking the first canonical basis vector and its repeated images by one obtains
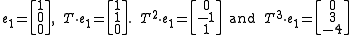
of which the first three are easily seen to be linearly independent, and therefore span all of . The last one then necessarily is a linear combination of the first three, in fact
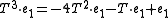, so that 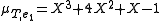. This is in fact also the minimal polynomial 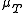and the characteristic polynomial 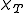: indeed 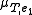divides 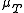which divides 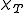, and since the first and last are of degree 3 and all are monic, they must all be the same. Another reason is that in general if any polynomial in annihilates a vector , then it also annihilates (just apply to the equation that says that it annihilates ), and therefore by iteration it annihilates the entire space generated by the iterated images by of ; in the current case we have seen that for that space is all of , so 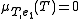. Indeed one verifies for the full matrix that 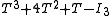is the null matrix: