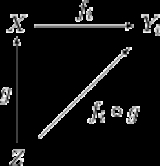
Initial topology
Encyclopedia
In general topology
and related areas of mathematics
, the initial topology (or weak topology or limit topology or projective topology) on a set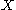
, with respect to a family of functions on 
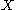, is the coarsest topology on X which makes those functions continuous.
The subspace topology
and product topology
constructions are both special cases of initial topologies. Indeed, the initial topology construction can be viewed as a generalization of these.
The dual
construction is called the final topology
.
(Yi)i∈I of topological space
s with functions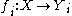
the initial topology τ on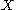
is the coarsest topology on X such that each
is continuous.
Explicitly, the initial topology may be described as the topology generated by
sets of the form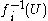
, where 
is an open set
in
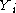. The sets 
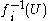are often called cylinder set
s.
: a function
from some space 
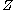to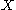 
is continuous if and only if 
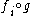is continuous for each i ∈ I.
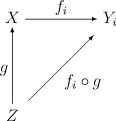
we know that any family of continuous maps fi : X → Yi determines a unique continuous map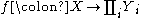
This map is known as the evaluation map.
A family of maps {fi: X → Yi} is said to separate points
in X if for all x ≠ y in X there exists some i such that fi(x) ≠ fi(y). Clearly, the family {fi} separates points if and only if the associated evaluation map f is injective.
The evaluation map f will be a topological embedding if and only if X has the initial topology determined by the maps {fi} and this family of maps separates points in X.
A family of maps {fi: X → Yi} separates points from closed sets in X if for all closed set
s A in X and all x not in A, there exists some i such that
where cl denoting the closure operator
.
It follows that whenever {fi} separates points from closed sets, the space X has the initial topology induced by the maps {fi}. The converse fails, since generally the cylinder sets will only form a subbase (and not a base) for the initial topology.
If the space X is a T0 space, then any collection of maps {fi} which separate points from closed sets in X must also separate points. In this case, the evaluation map will be an embedding.
, the initial topology construction can be described as follows. Let Y be the functor
from a discrete category
J to the category of topological spaces
Top which selects the spaces Yj for j in J. Let U be the usual forgetful functor
from Top to Set. The maps {fj} can then be thought of as a cone
from X to UY. That is, (X, f) is an object of Cone(UY)—the category of cones to UY.
The characteristic property of the initial topology is equivalent to the statement that there exists a universal morphism from the forgetful functor
to the cone (X, f). By placing the initial topology on X we therefore obtain a functor
which is right adjoint to the forgetful functor U′. In fact, I is a right-inverse to U′ since U′I is the identity functor on Cone(UY).
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the initial topology (or weak topology or limit topology or projective topology) on a set
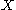, with respect to a family of functions on 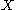, is the coarsest topology on X which makes those functions continuous.The subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
and product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
constructions are both special cases of initial topologies. Indeed, the initial topology construction can be viewed as a generalization of these.
The dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
construction is called the final topology
Final topology
In general topology and related areas of mathematics, the final topology on a set X, with respect to a family of functions into X, is the finest topology on X which makes those functions continuous.- Definition :Given a set X and a family of topological spaces Y_i with functionsf_i: Y_i \to Xthe...
.
Definition
Given a set X and an indexed familyIndexed family
In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
(Yi)i∈I of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s with functions
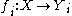
the initial topology τ on
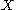is the coarsest topology on X such that eachis continuous.
Explicitly, the initial topology may be described as the topology generated by
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
sets of the form
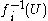, where is an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in
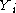. The sets 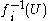are often called cylinder setCylinder set
In mathematics, a cylinder set is the natural open set of a product topology. Cylinder sets are particularly useful in providing the base of the natural topology of the product of a countable number of copies of a set...
s.
Examples
Several topological constructions can be regarded as special cases of the initial topology.- The subspace topologySubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
is the initial topology on the subspace with respect to the inclusion mapInclusion mapIn mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
. - The product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
is the initial topology with respect to the family of projection maps. - The inverse limitInverse limitIn mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of any inverse systemInverse systemIn mathematics, an inverse system in a category C is a functor from a small cofiltered category I to C. An inverse system is sometimes called a pro-object in C. The dual concept is a direct system.-The category of inverse systems:...
of spaces and continuous maps is the set-theoretic inverse limit together with the initial topology determined by the canonical morphisms. - The weak topologyWeak topologyIn mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
on a locally convex space is the initial topology with respect to the continuous linear forms of its dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
. - Given a family of topologies {τi} on a fixed set X the initial topology on X with respect to the functions idX : X → (X, τi) is the supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
(or join) of the topologies {τi} in the lattice of topologies on X. That is, the initial topology τ is the topology generated by the unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of the topologies {τi}. - A topological space is completely regular if and only if it has the initial topology with respect to its family of (boundedBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
) real-valued continuous functions. - Every topological space X has the initial topology with respect to the family of continuous functions from X to the Sierpiński spaceSierpinski spaceIn mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
.
Characteristic property
The initial topology on X can be characterized by the following universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: a function
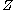from some space to 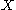is continuous if and only if 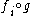is continuous for each i ∈ I.Evaluation
By the universal property of the product topologyProduct topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
we know that any family of continuous maps fi : X → Yi determines a unique continuous map
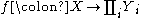
This map is known as the evaluation map.
A family of maps {fi: X → Yi} is said to separate points
Separating set
In mathematics a set of functions S from a set D to a set C is called a separating set for D or said to separate the points of D if for any two distinct elements x and y of D, there exists a function f in S so that f ≠ f.- Examples :* The singleton set consisting of the identity function on R...
in X if for all x ≠ y in X there exists some i such that fi(x) ≠ fi(y). Clearly, the family {fi} separates points if and only if the associated evaluation map f is injective.
The evaluation map f will be a topological embedding if and only if X has the initial topology determined by the maps {fi} and this family of maps separates points in X.
Separating points from closed sets
If a space X comes equipped with a topology, it is often useful to know whether or not the topology on X is the initial topology induced by some family of maps on X. This section gives a sufficient (but not necessary) condition.A family of maps {fi: X → Yi} separates points from closed sets in X if for all closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s A in X and all x not in A, there exists some i such that
where cl denoting the closure operator
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
.
- Theorem. A family of continuous maps {fi: X → Yi} separates points from closed sets if and only if the cylinder sets
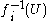, for U open in Yi, form a base for the topologyBase (topology)In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
on X.
It follows that whenever {fi} separates points from closed sets, the space X has the initial topology induced by the maps {fi}. The converse fails, since generally the cylinder sets will only form a subbase (and not a base) for the initial topology.
If the space X is a T0 space, then any collection of maps {fi} which separate points from closed sets in X must also separate points. In this case, the evaluation map will be an embedding.
Categorical description
In the language of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the initial topology construction can be described as follows. Let Y be the functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from a discrete category
Discrete category
In mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
J to the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
Top which selects the spaces Yj for j in J. Let U be the usual forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
from Top to Set. The maps {fj} can then be thought of as a cone
Cone (category theory)
In category theory, a branch of mathematics, the cone of a functor is an abstract notion used to define the limit of that functor. Cones make other appearances in category theory as well.-Definition:...
from X to UY. That is, (X, f) is an object of Cone(UY)—the category of cones to UY.
The characteristic property of the initial topology is equivalent to the statement that there exists a universal morphism from the forgetful functor
- U′ : Cone(Y) → Cone(UY)
to the cone (X, f). By placing the initial topology on X we therefore obtain a functor
- I : Cone(UY) → Cone(Y)
which is right adjoint to the forgetful functor U′. In fact, I is a right-inverse to U′ since U′I is the identity functor on Cone(UY).