
Zero set
Encyclopedia
In mathematics
, the zero set of a real-valued function
f : X → R (or more generally, a function taking values in some additive group
) is the subset
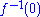 of X (the inverse image of {0}). In other words, the zero set of the function f is the subset of X on which
of X (the inverse image of {0}). In other words, the zero set of the function f is the subset of X on which 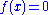 . The cozero set of f is the complement
. The cozero set of f is the complement
of the zero set of f (i.e. the subset of X on which f is nonzero).
Zero sets are important in several branches of geometry and topology.
, zero sets are defined with respect to continuous functions. Let X be a topological space
, and let A be a subset of X. Then A is a zero set in X if there exists a continuous function f : X → R such that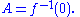
A cozero set in X is a subset whose complement is a zero set.
Every zero set is a closed set
and a cozero set is an open set
, but the converses does not always hold. In fact:
s. An important spacial case is the case that f is a smooth function
from Rp to Rn. If zero is a regular value of f then the zero-set of f is a smooth manifold of dimension m=p-n by the regular value theorem.
For example, the unit m-sphere
in Rm+1 is the zero set of the real-valued function f(x) = |x|2 - 1.
, an affine variety is the zero set of a polynomial
, or collection of polynomials. Similarly, a projective variety is the projectivization
of the zero set of a collection of homogeneous polynomial
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the zero set of a real-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f : X → R (or more generally, a function taking values in some additive group
Additive group
An additive group may refer to:*an abelian group, when it is written using the symbol + for its binary operation*a group scheme representing the underlying-additive-group functor...
) is the subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
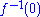 of X (the inverse image of {0}). In other words, the zero set of the function f is the subset of X on which
of X (the inverse image of {0}). In other words, the zero set of the function f is the subset of X on which 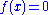 . The cozero set of f is the complement
. The cozero set of f is the complementComplement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the zero set of f (i.e. the subset of X on which f is nonzero).
Zero sets are important in several branches of geometry and topology.
Topology
In topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, zero sets are defined with respect to continuous functions. Let X be a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, and let A be a subset of X. Then A is a zero set in X if there exists a continuous function f : X → R such that
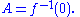
A cozero set in X is a subset whose complement is a zero set.
Every zero set is a closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and a cozero set is an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
, but the converses does not always hold. In fact:
- A topological space X is completely regular if and only if every closed set is the intersection of a family of zero sets in X. Equivalently, X is completely regular if and only if the cozero sets form a basis for X.
- A topological space is perfectly normal if and only if every closed set is a zero set (equivalently, every open set is a cozero set).
Differential geometry
In differential geometry, zero sets are frequently used to define manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. An important spacial case is the case that f is a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
from Rp to Rn. If zero is a regular value of f then the zero-set of f is a smooth manifold of dimension m=p-n by the regular value theorem.
For example, the unit m-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
in Rm+1 is the zero set of the real-valued function f(x) = |x|2 - 1.
Algebraic geometry
In algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, an affine variety is the zero set of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, or collection of polynomials. Similarly, a projective variety is the projectivization
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
of the zero set of a collection of homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s.

