
Moore plane
Encyclopedia
In mathematics
, the Moore plane, also sometimes called Niemytzki plane (or Nemytskii plane, Nemytskii's tangent disk topology) is a topological space
. It is a completely regular Hausdorff space
(also called Tychonoff space
) which is not normal
. It is named after Robert Lee Moore
and Viktor Vladimirovich Nemytskii.
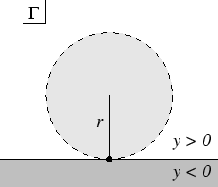 If
If  is the upper half-plane
is the upper half-plane  , then a topology
, then a topology
may be defined on by taking a local basis
by taking a local basis 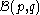 as follows:
as follows:
That is, the local basis is given by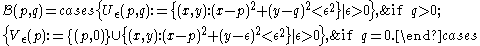
can be established by the following counting argument (which is very similar to the argument that the Sorgenfrey plane is not normal):
In fact, if X is a separable topological space having an uncountable closed discrete subspace, X cannot be normal.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Moore plane, also sometimes called Niemytzki plane (or Nemytskii plane, Nemytskii's tangent disk topology) is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. It is a completely regular Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
(also called Tychonoff space
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
) which is not normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. It is named after Robert Lee Moore
Robert Lee Moore
Robert Lee Moore was an American mathematician, known for his work in general topology and the Moore method of teaching university mathematics.-Life:...
and Viktor Vladimirovich Nemytskii.
Definition

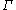 is the upper half-plane
is the upper half-plane  , then a topology
, then a topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
may be defined on
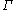 by taking a local basis
by taking a local basis 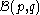 as follows:
as follows:- At points
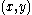 with
with 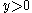 , the openOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
, the openOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
neighbourhoodsNeighbourhood (mathematics)In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
are the open discs in the plane which are small enough to lie within . This is just the subspace topologySubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
. This is just the subspace topologySubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
of the usual topology of the Euclidean plane.
- At points
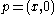 , the open neighbourhoods are sets
, the open neighbourhoods are sets 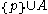 where A is an open disc in the upper half-plane which is tangent to the x axis at p.
where A is an open disc in the upper half-plane which is tangent to the x axis at p.
That is, the local basis is given by
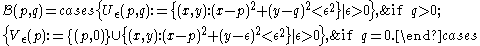
Properties
- The Moore plane
 is separable.
is separable. - The Moore plane is a completely regular Hausdorff spaceTychonoff spaceIn topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
(i.e. Tychonoff spaceTychonoff spaceIn topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
), which is not normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. - The subspace
 of
of 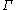 has, as its subspace topologySubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
has, as its subspace topologySubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
, the discrete topology. Thus, the Moore plane shows that a subspace of a separable space need not be separable. - The Moore plane is first countable, but not second countable or LindelöfLindelöf spaceIn mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
. - The Moore plane is not locally compact.
- The Moore plane is countably metacompact but not metacompact.
Proof that the Moore plane is not normal
The fact that this space M is not normalNormal
Normal may refer to:* Normality , conformance to an average* Norm , social norms, expected patterns of behavior studied within the context of sociology* Normal distribution , the Gaussian continuous probability distribution...
can be established by the following counting argument (which is very similar to the argument that the Sorgenfrey plane is not normal):
- On the one hand, the countable set
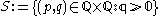 of points with rational coordinates is dense in M; hence every continuous function
of points with rational coordinates is dense in M; hence every continuous function 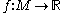 is determined by its restriction to
is determined by its restriction to  , so there can be at most
, so there can be at most  many continuous real-valued functions on M.
many continuous real-valued functions on M. - On the other hand, the real line
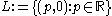 is a closed discrete subspace of M with
is a closed discrete subspace of M with  many points. So there are
many points. So there are 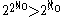 many continuous functions from L to
many continuous functions from L to 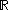 . Not all these functions can be extended to continuous functions on M.
. Not all these functions can be extended to continuous functions on M. - Hence M is not normal, because by the Tietze extension theorem all continuous functions defined on a closed subspace of a normal space can be extended to a continuous function on the whole space.
In fact, if X is a separable topological space having an uncountable closed discrete subspace, X cannot be normal.

