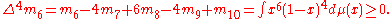Hausdorff moment problem
Encyclopedia
In mathematics
, the Hausdorff moment problem, named after Felix Hausdorff
, asks for necessary and sufficient conditions that a given sequence { mn : n = 0, 1, 2, ... }
be the sequence of moments

of some Borel measure μ supported on the closed unit interval [0, 1]. In the case m0 = 1, this is equivalent to the existence of a random variable
X supported on [0, 1], such that E Xn = mn.
The essential difference between this and other well-known moment problems is that this is on a bounded interval, whereas in the Stieltjes moment problem one considers a half-line [0, ∞), and in the Hamburger moment problem one considers the whole line (−∞, ∞).
In 1921, Hausdorff showed that { mn : n = 0, 1, 2, ... } is such a moment sequence if and only if the sequence is completely monotonic, i.e., its difference sequences satisfy the equation
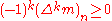
for all n,k ≤ 0. Here, Δ is the difference operator given by
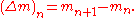
The necessity of this condition is easily seen by the identity
which is ≥ 0, being the integral of an almost sure non-negative function.
For example, it is necessary to have
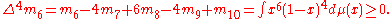
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hausdorff moment problem, named after Felix Hausdorff
Felix Hausdorff
Felix Hausdorff was a Jewish German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.-Life:Hausdorff studied at the University of Leipzig,...
, asks for necessary and sufficient conditions that a given sequence { mn : n = 0, 1, 2, ... }
be the sequence of moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...

of some Borel measure μ supported on the closed unit interval [0, 1]. In the case m0 = 1, this is equivalent to the existence of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X supported on [0, 1], such that E Xn = mn.
The essential difference between this and other well-known moment problems is that this is on a bounded interval, whereas in the Stieltjes moment problem one considers a half-line [0, ∞), and in the Hamburger moment problem one considers the whole line (−∞, ∞).
In 1921, Hausdorff showed that { mn : n = 0, 1, 2, ... } is such a moment sequence if and only if the sequence is completely monotonic, i.e., its difference sequences satisfy the equation
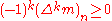
for all n,k ≤ 0. Here, Δ is the difference operator given by
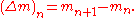
The necessity of this condition is easily seen by the identity

which is ≥ 0, being the integral of an almost sure non-negative function.
For example, it is necessary to have