
Hamburger moment problem
Encyclopedia
In mathematics
, the Hamburger moment problem, named after Hans Ludwig Hamburger
, is formulated as follows: given a sequence { mn : n = 1, 2, 3, ... }, does there exist a positive Borel measure μ on the real line such that
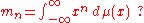
In other words, an affirmative answer to the problem means that { mn : n = 0, 1, 2, ... } is the sequence of moments
of some positive Borel measure μ.
The Stieltjes moment problem, Vorobyev moment problem, and the Hausdorff moment problem are similar but replace the real line by [0, +∞) (Stieltjes and Vorobyev; but Vorobyev formulates the problem in the terms of matrix theory), or a bounded interval (Hausdorff).
) if and only if the corresponding Hankel kernel on the nonnegative integers
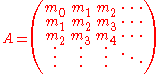
is positive definite, i.e.,

for an arbitrary sequence {cj}j ≥ 0 of complex numbers with finite support (i.e.
cj = 0 except for finitely many values of j).
The "only if" part of the claims can be verified by a direct calculation.
We sketch an argument for the converse. Let Z+ be the nonnegative integers and F0(Z+) denote the family of complex valued sequences with finite support. The positive Hankel kernel A induces a (possibly degenerate) sesquilinear product on the family of complex valued sequences with finite support. This in turn gives a Hilbert space
whose typical element is an equivalence class denoted by [f].
Let en be the element in F0(Z+) defined by en(m) = δnm. One notices that

Therefore the "shift" operator
T on , with T[en] = [en + 1], is symmetric.
, with T[en] = [en + 1], is symmetric.
On the other hand, the desired expression
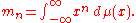
suggests that μ is the spectral measure of a self-adjoint operator
. If we can find a "function model" such that the symmetric operator T is multiplication by x
, then the spectral resolution of a self-adjoint extension
of T proves the claim.
A function model is given by the natural isomorphism from F0(Z+) to the family of polynomials, in one single real variable and complex coefficients: for n ≥ 0, identify en with xn. In the model, the operator T is multiplication by x and a densely defined symmetric operator. It can be shown that T always has self-adjoint extensions. Let

be one of them and μ be its spectral measure. So

On the other hand,
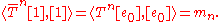
Consider the (n + 1)×(n + 1) Hankel matrix
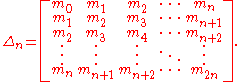
Positivity of A means that for each n, det(Δn) ≥ 0. If det(Δn) = 0, for some n, then
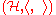
is finite dimensional and T is self-adjoint. So in this case the solution to the Hamburger moment problem is unique and μ, being the spectral measure of T, has finite support.
More generally, the solution is unique if there are constants C and D such that for all n, |mn|≤ CDnn! . This follows from the more general Carleman's condition
.
There are examples where the solution is not unique.
on the real line. The Gram–Schmidt procedure gives a basis of orthogonal polynomials in which the operator

has a tridiagonal Jacobi matrix representation. This in turn leads to a tridiagonal model of positive Hankel kernels.
An explicit calculation of the Cayley transform
of T shows the connection with what is called the Nevanlinna class of analytic functions on the left half plane. Passing to the non-commutative setting, this motivates Krein's formula which parametrizes the extensions of partial isometries.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hamburger moment problem, named after Hans Ludwig Hamburger
Hans Hamburger
Hans Ludwig Hamburger was a German mathematician. He was a professor at universities in Berlin, Cologne and Ankara....
, is formulated as follows: given a sequence { mn : n = 1, 2, 3, ... }, does there exist a positive Borel measure μ on the real line such that
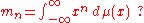
In other words, an affirmative answer to the problem means that { mn : n = 0, 1, 2, ... } is the sequence of moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of some positive Borel measure μ.
The Stieltjes moment problem, Vorobyev moment problem, and the Hausdorff moment problem are similar but replace the real line by [0, +∞) (Stieltjes and Vorobyev; but Vorobyev formulates the problem in the terms of matrix theory), or a bounded interval (Hausdorff).
Characterization
The Hamburger moment problem is solvable (that is, {mn} is a sequence of momentsMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
) if and only if the corresponding Hankel kernel on the nonnegative integers
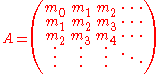
is positive definite, i.e.,

for an arbitrary sequence {cj}j ≥ 0 of complex numbers with finite support (i.e.
cj = 0 except for finitely many values of j).
The "only if" part of the claims can be verified by a direct calculation.
We sketch an argument for the converse. Let Z+ be the nonnegative integers and F0(Z+) denote the family of complex valued sequences with finite support. The positive Hankel kernel A induces a (possibly degenerate) sesquilinear product on the family of complex valued sequences with finite support. This in turn gives a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
whose typical element is an equivalence class denoted by [f].
Let en be the element in F0(Z+) defined by en(m) = δnm. One notices that

Therefore the "shift" operator
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
T on
 , with T[en] = [en + 1], is symmetric.
, with T[en] = [en + 1], is symmetric.On the other hand, the desired expression
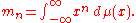
suggests that μ is the spectral measure of a self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
. If we can find a "function model" such that the symmetric operator T is multiplication by x
Multiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
, then the spectral resolution of a self-adjoint extension
Extensions of symmetric operators
In functional analysis, one is interested in extensions of symmetric operators acting on a Hilbert space. Of particular importance is the existence, and sometimes explicit constructions, of self-adjoint extensions. This problem arises, for example, when one needs to specify domains of...
of T proves the claim.
A function model is given by the natural isomorphism from F0(Z+) to the family of polynomials, in one single real variable and complex coefficients: for n ≥ 0, identify en with xn. In the model, the operator T is multiplication by x and a densely defined symmetric operator. It can be shown that T always has self-adjoint extensions. Let

be one of them and μ be its spectral measure. So

On the other hand,
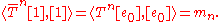
Uniqueness of solutions
The solutions form a convex set, so the problem has either infinitely many solutions or a unique solution.Consider the (n + 1)×(n + 1) Hankel matrix
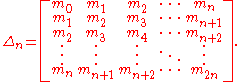
Positivity of A means that for each n, det(Δn) ≥ 0. If det(Δn) = 0, for some n, then
is finite dimensional and T is self-adjoint. So in this case the solution to the Hamburger moment problem is unique and μ, being the spectral measure of T, has finite support.
More generally, the solution is unique if there are constants C and D such that for all n, |mn|≤ CDnn! . This follows from the more general Carleman's condition
Carleman's condition
In mathematics, Carleman's condition is a sufficient condition for the determinacy of the moment problem.-Hamburger moment problem:For the Hamburger moment problem, the theorem, proved by Torsten Carleman, states the following:...
.
There are examples where the solution is not unique.
Further results
One can see that the Hamburger moment problem is intimately related to orthogonal polynomialsOrthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
on the real line. The Gram–Schmidt procedure gives a basis of orthogonal polynomials in which the operator

has a tridiagonal Jacobi matrix representation. This in turn leads to a tridiagonal model of positive Hankel kernels.
An explicit calculation of the Cayley transform
Cayley transform
In mathematics, the Cayley transform, named after Arthur Cayley, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. In complex analysis, the Cayley transform is a conformal mapping in...
of T shows the connection with what is called the Nevanlinna class of analytic functions on the left half plane. Passing to the non-commutative setting, this motivates Krein's formula which parametrizes the extensions of partial isometries.

