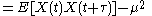Autocovariance
Encyclopedia
In statistics
, given a real stochastic process
X(t), the autocovariance is the covariance
of the variable with itself, i.e. the variance
of the variable against a time-shifted version of itself. If the process has the mean
E[Xt] = μt, then the autocovariance is given by
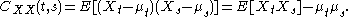
where E is the expectation
operator.
, then the following conditions are true:
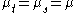for all t, s
and
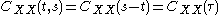
where
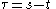
is the lag time, or the amount of time by which the signal has been shifted.
As a result, the autocovariance becomes
where RXX represents the autocorrelation
in the signal processing sense.
σ2, the autocovariance C becomes the autocorrelation
coefficient function c,
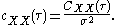
The autocovariance function is itself a version of the autocorrelation function with the mean level removed. If the signal has a mean of 0, the autocovariance and autocorrelation functions are identical .
However, often the autocovariance is called autocorrelation even if this normalization has not been performed.
The autocovariance can be thought of as a measure of how similar a signal is to a time-shifted version of itself with an autocovariance of σ2 indicating perfect correlation at that lag. The normalisation with the variance will put this into the range [−1, 1].
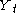
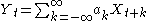
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, given a real stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
X(t), the autocovariance is the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
of the variable with itself, i.e. the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the variable against a time-shifted version of itself. If the process has the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
E[Xt] = μt, then the autocovariance is given by
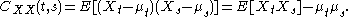
where E is the expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
operator.
Stationarity
If X(t) is stationary processStationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
, then the following conditions are true:
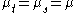for all t, sand
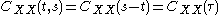
where
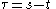
is the lag time, or the amount of time by which the signal has been shifted.
As a result, the autocovariance becomes
where RXX represents the autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
in the signal processing sense.
Normalization
When normalized by dividing by the varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
σ2, the autocovariance C becomes the autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
coefficient function c,
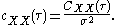
The autocovariance function is itself a version of the autocorrelation function with the mean level removed. If the signal has a mean of 0, the autocovariance and autocorrelation functions are identical .
However, often the autocovariance is called autocorrelation even if this normalization has not been performed.
The autocovariance can be thought of as a measure of how similar a signal is to a time-shifted version of itself with an autocovariance of σ2 indicating perfect correlation at that lag. The normalisation with the variance will put this into the range [−1, 1].
Properties
The autocovariance of a linearly filtered process
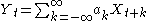
- is
