Time constant
Encyclopedia
In physics
and engineering
, the time constant, usually denoted by the Greek
letter
(tau), is the risetime characterizing the response to a time-varying input of a first-order, linear time-invariant
(LTI) system.Concretely, a first-order LTI system is a system that can be modeled by a single first order differential equation
in time. Examples include the simplest single-stage electrical RC circuits and RL circuits. The time constant is the main characteristic unit of a first-order LTI (linear time-invariant) system.
In the time domain, the usual choice to explore the time response is through the step response
to a step input
, or the impulse response
to a Dirac delta function
input. In the frequency domain (for example, looking at the Fourier transform
of the step response, or using an input that is a simple sinusoidal function of time) the time constant also determines the bandwidth of a first-order time-invariant system, that is, the frequency at which the output signal power drops to half the value it has at low frequencies.
The time constant also is used to characterize the frequency response of various signal processing
systems – magnetic tape
s, radio transmitters and receivers, record cutting and replay equipment, and digital filter
s – which can be modeled or approximated by first-order LTI systems. Other examples include time constant used in control system
s for integral and derivative action controllers, which are often pneumatic, rather than electrical.
Time constants are a feature of the lumped system analysis (lumped capacity analysis method) for thermal systems, used when objects cool or warm uniformly under the influence of convective cooling or warming.
Physically, the constant represents the time it takes the system's step response
to reach
of its final (asymptotic) value. In radioactive decay the time constant is called the decay constant (λ), and it represents both the mean lifetime of a decaying system (such as an atom) before it decays, or the time it takes for all but 36.8% of the atoms to decay. For this reason, the time constant is longer than the half-life
, which is the time for only 50% of the atoms to decay.
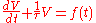
where τ represents the exponential decay constant and V is a function of time t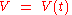
The right-hand side is the forcing function f(t) describing an external driving function of time, which can be regarded as the system input, to which V(t) is the response, or system output. Typical choices for f(t) are the Heaviside step function
, often denoted by u(t):
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, the time constant, usually denoted by the Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
letter
(tau), is the risetime characterizing the response to a time-varying input of a first-order, linear time-invariantLTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
(LTI) system.Concretely, a first-order LTI system is a system that can be modeled by a single first order differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
in time. Examples include the simplest single-stage electrical RC circuits and RL circuits. The time constant is the main characteristic unit of a first-order LTI (linear time-invariant) system.
In the time domain, the usual choice to explore the time response is through the step response
Step response
The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from...
to a step input
Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
, or the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
to a Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
input. In the frequency domain (for example, looking at the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the step response, or using an input that is a simple sinusoidal function of time) the time constant also determines the bandwidth of a first-order time-invariant system, that is, the frequency at which the output signal power drops to half the value it has at low frequencies.
The time constant also is used to characterize the frequency response of various signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
systems – magnetic tape
Magnetic tape
Magnetic tape is a medium for magnetic recording, made of a thin magnetizable coating on a long, narrow strip of plastic. It was developed in Germany, based on magnetic wire recording. Devices that record and play back audio and video using magnetic tape are tape recorders and video tape recorders...
s, radio transmitters and receivers, record cutting and replay equipment, and digital filter
Digital filter
In electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
s – which can be modeled or approximated by first-order LTI systems. Other examples include time constant used in control system
Control system
A control system is a device, or set of devices to manage, command, direct or regulate the behavior of other devices or system.There are two common classes of control systems, with many variations and combinations: logic or sequential controls, and feedback or linear controls...
s for integral and derivative action controllers, which are often pneumatic, rather than electrical.
Time constants are a feature of the lumped system analysis (lumped capacity analysis method) for thermal systems, used when objects cool or warm uniformly under the influence of convective cooling or warming.
Physically, the constant represents the time it takes the system's step response
Step response
The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from...
to reach
of its final (asymptotic) value. In radioactive decay the time constant is called the decay constant (λ), and it represents both the mean lifetime of a decaying system (such as an atom) before it decays, or the time it takes for all but 36.8% of the atoms to decay. For this reason, the time constant is longer than the half-lifeHalf-life
Half-life, abbreviated t½, is the period of time it takes for the amount of a substance undergoing decay to decrease by half. The name was originally used to describe a characteristic of unstable atoms , but it may apply to any quantity which follows a set-rate decay.The original term, dating to...
, which is the time for only 50% of the atoms to decay.
Differential equation
First order LTI systems are characterized by the differential equation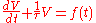where τ represents the exponential decay constant and V is a function of time t
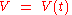
The right-hand side is the forcing function f(t) describing an external driving function of time, which can be regarded as the system input, to which V(t) is the response, or system output. Typical choices for f(t) are the Heaviside step function
Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
, often denoted by u(t):
-
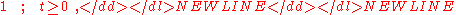
the impulse functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
, often denoted by δ(t), and also the sinusoidal input function:
or
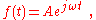
where A is the amplitude of the forcing function, f is the frequency in Hertz, and ω = 2π f is the frequency in radians per second.
Example solution
An example solution to the differential equation with initial value V0 and no forcing function is
where
is the initial value of V. Thus, the response is an exponential decay with time constant τ.
Discussion
Suppose
This behavior is referred to as a "decaying" exponential function. The time
(tau) is referred to as the "time constant" and can be used (as in this case) to indicate how rapidly an exponential function decays.
Here:- t = time (generally
in control engineering) - V0 = initial value (see "specific cases" below).
Specific cases
- 1) Let
; then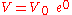 
, and so 
- 2) Let
; then 
, ≈ 
- 3) Let
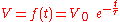, and so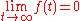 
- 4) Let
; then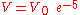 
, ≈ 
After a period of one time constant the function reaches e−1 = approximately 37% of its initial value. In case 4, after five time constants the function reaches a value less than 1% of its original. In most cases this 1% threshold is considered sufficient to assume that the function has decayed to zero - as a rule of thumb, in control engineering a stable system is one that exhibits such an overall damped behavior.
Relation of time constant to bandwidth
Suppose the forcing function is chosen as sinusoidal so:
(Response to a real cosine or sine wave input can be obtained by taking the real or imaginary part of the final result by virtue of Euler's formulaEuler's formulaEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
.)
The general solution to this equation for times t ≥ 0 s, assuming V(t=0) = V0 is:
For long times the decaying exponentials become negligible and the so-called steady-state solution or long-time solution is:
The magnitude of this response is: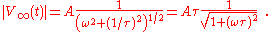
By convention, the bandwidth of this system is the frequency where |V∞|2 drops to half-value, or where ωτ = 1. This is the usual bandwidth convention, defined as the frequency range where power drops by less than half (at most −3 dB). Using the frequency in hertz, rather than radians/s (ω = 2πf):
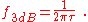
The notation f3dB stems from the expression of power in decibels and the observation that half-power corresponds to a drop in the value of |V∞| by a factor of 1/√2 or by 3 decibels.
Thus, the time constant determines the bandwidth of this system.
Step response with arbitrary initial conditions
Suppose the forcing function is chosen as a step input so:
with u(t) the Heaviside step function. The general solution to this equation for times t ≥ 0 s, assuming V(t=0) = V0 is:
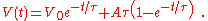
(It may be observed that this response is the ω → 0 limit of the above response to a sinusoidal input.)
The long-time solution is time independent and independent of initial conditions: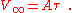
The time constant remains the same for the same system regardless of the starting conditions. Simply stated, a system approaches its final, steady-state situation at a constant rate, regardless of how close it is to that value at any arbitrary starting point.
For example, consider an electric motor whose startup is well modeled by a first-order LTI system. Suppose that when started from rest, the motor takes ⅛ of a second to reach 63% of its nominal speed of 100 RPM, or 63 RPM—a shortfall of 37 RPM. Then it will be found that after the next ⅛ of a second, the motor has sped up an additional 23 RPM, which equals 63% of that 37 RPM difference. This brings it to 86 RPM—still 14 RPM low. After a third ⅛ of a second, the motor will have gained an additional 9 RPM (63% of that 14 RPM difference), putting it at 95 RPM.
In fact, given any initial speed s ≤ 100 RPM, ⅛ of a second later this particular motor will have gained an additional .63 × (100 − s) RPM.
Time constants in electrical circuits
In an RL circuitRL circuitA resistor-inductor circuit ', or RL filter or RL network, is one of the simplest analogue infinite impulse response electronic filters. It consists of a resistor and an inductor, either in series or in parallel, driven by a voltage source.-Introduction:The fundamental passive linear circuit...
composed of a single resistor and inductor, the time constant
(in secondSecondThe second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
s) is
where R is the resistanceElectrical resistanceThe electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
(in ohmOhmThe ohm is the SI unit of electrical resistance, named after German physicist Georg Simon Ohm.- Definition :The ohm is defined as a resistance between two points of a conductor when a constant potential difference of 1 volt, applied to these points, produces in the conductor a current of 1 ampere,...
s) and L is the inductanceInductanceIn electromagnetism and electronics, inductance is the ability of an inductor to store energy in a magnetic field. Inductors generate an opposing voltage proportional to the rate of change in current in a circuit...
(in henries).
Similarly, in an RC circuitRC circuitA resistor–capacitor circuit ', or RC filter or RC network, is an electric circuit composed of resistors and capacitors driven by a voltage or current source...
composed of a single resistor and capacitor, the time constant
(in seconds) is:
where R is the resistance (in ohmOhmThe ohm is the SI unit of electrical resistance, named after German physicist Georg Simon Ohm.- Definition :The ohm is defined as a resistance between two points of a conductor when a constant potential difference of 1 volt, applied to these points, produces in the conductor a current of 1 ampere,...
s) and C is the capacitanceCapacitanceIn electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor...
(in faradFaradThe farad is the SI unit of capacitance. The unit is named after the English physicist Michael Faraday.- Definition :A farad is the charge in coulombs which a capacitor will accept for the potential across it to change 1 volt. A coulomb is 1 ampere second...
s).
Of course, electrical circuits are usually much more complex than these examples, and may exhibit multiple time constants (See Step responseStep responseThe step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from...
and Pole splittingPole splittingPole splitting is a phenomenon exploited in some forms of frequency compensation used in an electronic amplifier. When a capacitor is introduced between the input and output sides of the amplifier with the intention of moving the pole lowest in frequency to lower frequencies, pole splitting causes...
for some examples.) In the case where feedback is present, a system may exhibit unstable, increasing oscillations. In addition, physical electrical circuits are seldom truly linear systems except for very low amplitude excitations; however, the approximation of linearity is widely used.
Thermal time constant
Time constants are a feature of the lumped system analysis (lumped capacity analysis method) for thermal systems, used when objects cool or warm uniformly under the influence of convective cooling or warmingConvective heat transferConvective heat transfer, often referred to as convection, is the transfer of heat from one place to another by the movement of fluids. The presence of bulk motion of the fluid enhances the heat transfer between the solid surface and the fluid. Convection is usually the dominant form of heat...
. In this case, the heat transfer from the body to the ambient at a given time is proportional to the temperature difference between the body and the ambient:
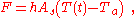
where h is heat transfer coefficient, and As is the surface area, T(t) = body temperature at time t, and Ta is the constant ambient temperature. The positive sign indicates the convention that F is positive when heat is leaving the body because its temperature is higher than the ambient temperature (F is an outward flux). If heat is lost to the ambient, this heat transfer leads to a drop in temperature of the body given by:
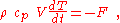
where ρ = density, cp = specific heat and V is the body volume. The negative sign indicates the temperature drops when the heat transfer is outward from the body (that is, when F > 0). Equating these two expressions for the heat transfer,
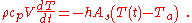
Evidently, this is a first-order LTI system that can be cast in the form:
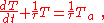
with
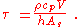
In other words, the time constant says that larger masses ρV and larger heat capacities cp lead to slower changes in temperature, while larger surface areas As and better heat transfer h lead to faster temperature changes.
Comparison with the introductory differential equation suggests the possible generalization to time-varying ambient temperatures Ta. However, retaining the simple constant ambient example, by substituting the variable ΔT ≡ (T − Ta), one finds:
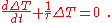
Systems for which cooling satisfies the above exponential equation are said to satisfy Newton's law of cooling. The solution to this equation suggests that, in such systems, the difference between the temperature of the system and its surroundings ΔT as a function of time t, is given by:
where ΔT0 is the initial temperature difference, at time t= 0. In words, the body assumes the same temperature as the ambient at an exponentially slow rate determined by the time constant.
Time constants in neurobiology
In an action potentialAction potentialIn physiology, an action potential is a short-lasting event in which the electrical membrane potential of a cell rapidly rises and falls, following a consistent trajectory. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, and...
(or even in a passive spread of signal) in a neuronNeuronA neuron is an electrically excitable cell that processes and transmits information by electrical and chemical signaling. Chemical signaling occurs via synapses, specialized connections with other cells. Neurons connect to each other to form networks. Neurons are the core components of the nervous...
, the time constant
is
where rm is the resistance across the membrane and cm is the capacitanceCapacitanceIn electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor...
of the membrane.
The resistance across the membrane is a function of the number of open ion channels and the capacitance is a function of the properties of the lipid bilayerLipid bilayerThe lipid bilayer is a thin membrane made of two layers of lipid molecules. These membranes are flat sheets that form a continuous barrier around cells. The cell membrane of almost all living organisms and many viruses are made of a lipid bilayer, as are the membranes surrounding the cell nucleus...
.
The time constant is used to describe the rise and fall of the action potentialAction potentialIn physiology, an action potential is a short-lasting event in which the electrical membrane potential of a cell rapidly rises and falls, following a consistent trajectory. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, and...
, where the rise is described by
and the fall is described by
Where voltageVoltageVoltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
is in millivolts, time is in seconds, and
is in seconds.
Vmax is defined as the maximum voltage attained in the action potential, where
where rm is the resistance across the membrane and I is the current.
Setting for t =
for the rise sets V(t) equal to 0.63Vmax. This means that the time constant is the time elapsed after 63% of Vmax has been reached
Setting for t =
for the fall sets V(t) equal to 0.37Vmax, meaning that the time constant is the time elapsed after it has fallen to 37% of Vmax.
The larger a time constant is, the slower the rise or fall of the potential of neuron. A long time constant can result in temporal summation, or the algebraic summation of repeated potentials.
Exponential decay
In exponential decay, such as of a radioactiveRadioactive decayRadioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles . The emission is spontaneous, in that the atom decays without any physical interaction with another particle from outside the atom...
isotope, the time constant can be interpreted as the mean lifetime. The half-lifeHalf-lifeHalf-life, abbreviated t½, is the period of time it takes for the amount of a substance undergoing decay to decrease by half. The name was originally used to describe a characteristic of unstable atoms , but it may apply to any quantity which follows a set-rate decay.The original term, dating to...
THL is related to the exponential time constant
by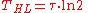
The reciprocal of the time constant is called the decay constant, and is denoted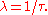
Meteorological sensors
A time constant is the amount of time it takes for a meteorological sensor to respond to a rapid change in a measurand until it is measuring values within the accuracy tolerance usually expected of the sensor.
This most often applies to measurements of temperature, dewpoint temperature, humidity and air pressure. RadiosondeRadiosondeA radiosonde is a unit for use in weather balloons that measures various atmospheric parameters and transmits them to a fixed receiver. Radiosondes may operate at a radio frequency of 403 MHz or 1680 MHz and both types may be adjusted slightly higher or lower as required...
s are especially affected due to their rapid increase in altitude.
See also
- RC time constantRC time constantIn an RC circuit, the value of the time constant is equal to the product of the circuit resistance and the circuit capacitance , i.e. \tau = R × C. It is the time required to charge the capacitor, through the resistor, to 63.2 percent of full charge; or to discharge it to 36.8 percent of its...
- Cutoff frequencyCutoff frequencyIn physics and electrical engineering, a cutoff frequency, corner frequency, or break frequency is a boundary in a system's frequency response at which energy flowing through the system begins to be reduced rather than passing through.Typically in electronic systems such as filters and...
- Exponential decay
- Length constantLength constantLength constant is a constant used in neurobiology signified by the Greek letter lambda . The longer a length constant is, the bigger the effect a potential will have along the cell...
- Rise timeRise timeIn electronics, when describing a voltage or current step function, rise time refers to the time required for a signal to change from a specified low value to a specified high value...
- Fall timeFall timeIn electronics, fall time \scriptstyle t_f\, is the time required for the amplitude of a pulse to decrease from a specified value to another specified value...
- Frequency responseFrequency responseFrequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
- Impulse responseImpulse responseIn signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
- Step responseStep responseThe step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from...
- Transition timeTransition timeThe transition time \scriptstyle t_t\, is the time a dynamical system needs to switch between two different stable states, when responding to a stable input signal. In a logic circuit undergoing a change of state, it identifies the rise time or the fall time of the output voltage...
- Settling timeSettling timeThe settling time of an amplifier or other output device is the time elapsed from the application of an ideal instantaneous step input to the time at which the amplifier output has entered and remained within a specified error band, usually symmetrical about the final value.Settling time includes a...
External links
- t = time (generally
