Partial autocorrelation function
Encyclopedia
In time series analysis, the partial autocorrelation function (PACF) plays an important role in data analyses aimed at identifying the extent of the lag in an autoregressive model
. The use of this function was introduced as part of the Box-Jenkins
approach to time series modelling, where by plotting the partial autocorrelative functions one could determine the appropriate lags p in an AR(p) model
or in an extended ARIMA
(p,d,q) model.
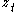, the partial autocorrelation of lag k, denoted 
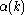, is the autocorrelation
between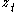
and 
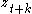with the linear dependence of 
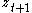through to 
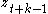removed; equivalently, it is the autocorrelation between 
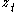and 
that is not accounted for by lags 1 to k − 1, inclusive.
where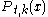
denotes the projection of 
onto the space spanned by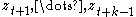 
.
There are algorithms, not discussed here, for estimating the partial autocorrelation based on the sample autocorrelations. See (Box, Jenkins, and Reinsel 2008) or (Brockwell and Davis, 2009) for the mathematical details. These algorithms derive from the exact theoretical relation between the partial autocorrelation function and the autocorrelation function.
Partial autocorrelation plots (Box and Jenkins, Chapter 3.2, 2008) are a commonly used tool for identifying the order of an autoregressive model
. The partial autocorrelation of an AR(p) process is zero at lag p + 1 and greater. If the sample autocorrelation plot indicates that an AR model may be appropriate, then the sample partial autocorrelation plot is examined to help identify the order. One looks for the point on the plot where the partial autocorrelations for all higher lags are essentially zero. Placing on the plot an indication of the sampling uncertainty of the sample PACF is helpful for this purpose: this is usually constructed on the basis that the true value of the PACF, at any given positive lag, is zero. This can be formalised as described below.
An approximate test that a given partial correlation is zero (at a 5% significance level) is given by comparing the sample partial autocorrelations against the critical region with upper and lower limits given by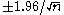
, where n is the record length (number of points) of the time-series being analysed. This approximation relies on the assumption that the record length is moderately large (say n>30) and that the underlying process has a multivariate normal distribution.
Autoregressive model
In statistics and signal processing, an autoregressive model is a type of random process which is often used to model and predict various types of natural phenomena...
. The use of this function was introduced as part of the Box-Jenkins
Box-Jenkins
In time series analysis, the Box–Jenkins methodology, named after the statisticians George Box and Gwilym Jenkins, applies autoregressive moving average ARMA or ARIMA models to find the best fit of a time series to past values of this time series, in order to make forecasts.-Modeling approach:The...
approach to time series modelling, where by plotting the partial autocorrelative functions one could determine the appropriate lags p in an AR(p) model
Autoregressive model
In statistics and signal processing, an autoregressive model is a type of random process which is often used to model and predict various types of natural phenomena...
or in an extended ARIMA
Autoregressive integrated moving average
In statistics and econometrics, and in particular in time series analysis, an autoregressive integrated moving average model is a generalization of an autoregressive moving average model. These models are fitted to time series data either to better understand the data or to predict future points...
(p,d,q) model.
Description
Given a time series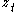, the partial autocorrelation of lag k, denoted 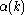, is the autocorrelationAutocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
between
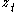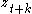and with the linear dependence of 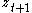through to 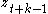removed; equivalently, it is the autocorrelation between 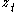and that is not accounted for by lags 1 to k − 1, inclusive.
where
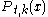denotes the projection of onto the space spanned by 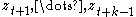.There are algorithms, not discussed here, for estimating the partial autocorrelation based on the sample autocorrelations. See (Box, Jenkins, and Reinsel 2008) or (Brockwell and Davis, 2009) for the mathematical details. These algorithms derive from the exact theoretical relation between the partial autocorrelation function and the autocorrelation function.
Partial autocorrelation plots (Box and Jenkins, Chapter 3.2, 2008) are a commonly used tool for identifying the order of an autoregressive model
Autoregressive model
In statistics and signal processing, an autoregressive model is a type of random process which is often used to model and predict various types of natural phenomena...
. The partial autocorrelation of an AR(p) process is zero at lag p + 1 and greater. If the sample autocorrelation plot indicates that an AR model may be appropriate, then the sample partial autocorrelation plot is examined to help identify the order. One looks for the point on the plot where the partial autocorrelations for all higher lags are essentially zero. Placing on the plot an indication of the sampling uncertainty of the sample PACF is helpful for this purpose: this is usually constructed on the basis that the true value of the PACF, at any given positive lag, is zero. This can be formalised as described below.
An approximate test that a given partial correlation is zero (at a 5% significance level) is given by comparing the sample partial autocorrelations against the critical region with upper and lower limits given by
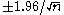, where n is the record length (number of points) of the time-series being analysed. This approximation relies on the assumption that the record length is moderately large (say n>30) and that the underlying process has a multivariate normal distribution.See also
- Partial correlationPartial correlationIn probability theory and statistics, partial correlation measures the degree of association between two random variables, with the effect of a set of controlling random variables removed.-Formal definition:...
- Autocorrelation function
- Box–Jenkins