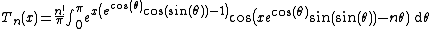Touchard polynomials
Encyclopedia
The Touchard polynomials, studied by , also called the exponential polynomials, comprise a polynomial sequence
of binomial type defined by
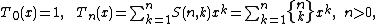
where S(n, k) is a Stirling number of the second kind, i.e., it is the number of partitions of a set
of size n into k disjoint non-empty subsets. (The second notation above, with { braces }, was introduced by Donald Knuth
.) The value at 1 of the nth Touchard polynomial is the nth Bell number, i.e., the number of partitions of a set
of size n:
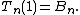
If X is a random variable
with a Poisson distribution
with expected value λ, then its nth moment is E(Xn) = Tn(λ), leading to the definition:
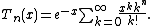
Using this fact one can quickly prove that this polynomial sequence
is of binomial type, i.e., it satisfies the sequence of identities:
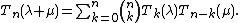
The Touchard polynomials make up the only polynomial sequence of binomial type in which the coefficient of the 1st-degree term of every polynomial is 1.

The Touchard polynomials satisfy the Rodrigues-like formula:

The Touchard polynomials satisfy the recursion
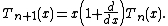
And
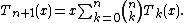
In case x = 1, this reduces to the recursion formula for the Bell numbers.
Using the Umbral notation Tn(x)=Tn(x),these formulas become:
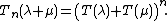

The generating function
of the Touchard polynomials is

And a contour-integral representation is
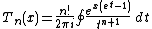
The Touchard polynomials (and thereby the Bell numbers) can be generalized, using the real part of the above integral, to non-integer order:
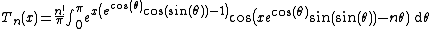
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
of binomial type defined by
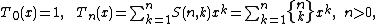
where S(n, k) is a Stirling number of the second kind, i.e., it is the number of partitions of a set
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of size n into k disjoint non-empty subsets. (The second notation above, with { braces }, was introduced by Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
.) The value at 1 of the nth Touchard polynomial is the nth Bell number, i.e., the number of partitions of a set
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of size n:
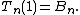
If X is a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with expected value λ, then its nth moment is E(Xn) = Tn(λ), leading to the definition:
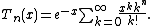
Using this fact one can quickly prove that this polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
is of binomial type, i.e., it satisfies the sequence of identities:
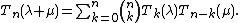
The Touchard polynomials make up the only polynomial sequence of binomial type in which the coefficient of the 1st-degree term of every polynomial is 1.

The Touchard polynomials satisfy the Rodrigues-like formula:

The Touchard polynomials satisfy the recursion
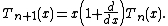
And
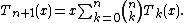
In case x = 1, this reduces to the recursion formula for the Bell numbers.
Using the Umbral notation Tn(x)=Tn(x),these formulas become:
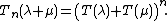

The generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
of the Touchard polynomials is

And a contour-integral representation is
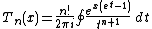
The Touchard polynomials (and thereby the Bell numbers) can be generalized, using the real part of the above integral, to non-integer order: