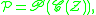Stirling numbers and exponential generating functions
Encyclopedia
The use of exponential generating functions (EGFs) to study the properties of Stirling numbers is a classical exercise in combinatorics
and possibly the canonical example of how symbolic combinatorics
, the method that encapsulates the fundamental theorem of combinatorial enumeration
, is used. It also illustrates the parallels in the construction of these two types of numbers, lending support to the binomial-style notation that is used for them.
This article uses the coefficient extraction operator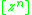
for formal power series
, as well as the (labelled) operators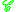
(for cycles) and 
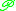(for sets) on combinatorial classes, which are explained on the pages for symbolic combinatorics
and the fundamental theorem of combinatorial enumeration
. Quite simply, given a combinatorial class, the cycle operator creates the class obtained by placing objects from the source class along a cycle of some length, where cyclical symmetries are taken into account, and the set operator creates the class obtained by placing objects from the source class in a set (symmetries from the symmetric group, i.e. an "unstructured bag".) The two combinatorial classes (shown without additional markers) are
and
where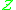
is the singleton class.
Warning: The notation used here for the Stirling numbers is not that of the Wikipedia articles on Stirling numbers, square brackets denote the signed Stirling numbers here.
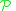of permutations is given by
where the singletion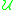
marks cycles. This decomposition is examined in some detail on the page on the statistics of random permutations
.
Translating to generating functions we obtain the mixed generating function of the unsigned Stirling numbers of the first kind:
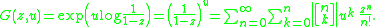
Now the signed Stirling numbers of the first kind are obtained from the unsigned ones through the relation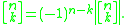
Hence the generating function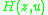
of these numbers is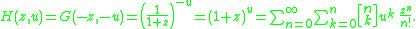
A variety of identities may be derived by manipulating this generating function
:
In particular, the order of summation may be exchanged, and derivatives taken, and then z or u may be fixed.
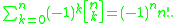
This formula holds because the exponential generating function of the sum is
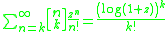
where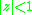
(the singularity nearest to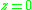 
of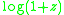
is at 
)
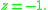This relation holds because
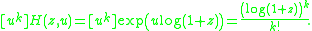
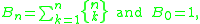
i.e. the Bell numbers. The fundamental theorem of combinatorial enumeration
applies (labelled case).
The set
of partitions into non-empty subsets is given by ("set of non-empty sets of singletons")
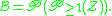
This decomposition is entirely analogous to the construction of the set
of permutations from cycles, which is given by
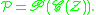
and yields the Stirling numbers of the first kind. Hence the name "Stirling numbers of the second kind."
The decomposition is equivalent to the EGF
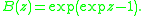
Differentiate to obtain
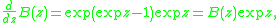
which implies that
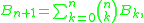
by convolution of exponential generating functions and because differentiating an EGF drops the first coefficient and shifts Bn+1 to z n/n! .
The EGF of the Stirling numbers of the second kind is obtained by marking every subset that goes into the partition with the term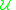
, giving
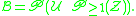
Translating to generating functions, we obtain
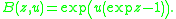
This EGF yields the formula for the Stirling numbers of the second kind:
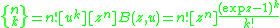
or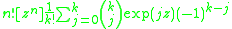
which simplifies to
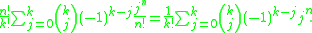
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and possibly the canonical example of how symbolic combinatorics
Symbolic combinatorics
In mathematics, symbolic combinatorics is one of the many techniques of counting combinatorial objects. It uses the internal structure of the objects to derive formulas for their generating functions. This particular theory is due to Philippe Flajolet and Robert Sedgewick. This article describes...
, the method that encapsulates the fundamental theorem of combinatorial enumeration
Fundamental theorem of combinatorial enumeration
The fundamental theorem of combinatorial enumeration is a theorem in combinatorics that solves the enumeration problem of labelled and unlabelled combinatorial classes.The unlabelled case is based on the Pólya enumeration theorem....
, is used. It also illustrates the parallels in the construction of these two types of numbers, lending support to the binomial-style notation that is used for them.
This article uses the coefficient extraction operator
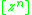for formal power seriesFormal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
, as well as the (labelled) operators
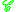(for cycles) and 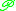(for sets) on combinatorial classes, which are explained on the pages for symbolic combinatoricsSymbolic combinatorics
In mathematics, symbolic combinatorics is one of the many techniques of counting combinatorial objects. It uses the internal structure of the objects to derive formulas for their generating functions. This particular theory is due to Philippe Flajolet and Robert Sedgewick. This article describes...
and the fundamental theorem of combinatorial enumeration
Fundamental theorem of combinatorial enumeration
The fundamental theorem of combinatorial enumeration is a theorem in combinatorics that solves the enumeration problem of labelled and unlabelled combinatorial classes.The unlabelled case is based on the Pólya enumeration theorem....
. Quite simply, given a combinatorial class, the cycle operator creates the class obtained by placing objects from the source class along a cycle of some length, where cyclical symmetries are taken into account, and the set operator creates the class obtained by placing objects from the source class in a set (symmetries from the symmetric group, i.e. an "unstructured bag".) The two combinatorial classes (shown without additional markers) are
- permutations (for unsigned Stirling numbers of the first kind):
and
- set partitions into non-empty subsets (for Stirling numbers of the second kind):
where
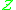is the singleton class.Warning: The notation used here for the Stirling numbers is not that of the Wikipedia articles on Stirling numbers, square brackets denote the signed Stirling numbers here.
Stirling numbers of the first kind
The unsigned Stirling numbers of the first kind count the number of permutations of [n] with k cycles. A permutation is a set of cycles, and hence the set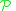 of permutations is given bywhere the singletion
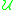marks cycles. This decomposition is examined in some detail on the page on the statistics of random permutationsRandom permutation statistics
The statistics of random permutations, such as the cycle structure of a random permutation are of fundamental importance in the analysis of algorithms, especially of sorting algorithms, which operate on random permutations. Suppose, for example, that we are using quickselect to select a random...
.
Translating to generating functions we obtain the mixed generating function of the unsigned Stirling numbers of the first kind:
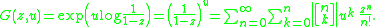
Now the signed Stirling numbers of the first kind are obtained from the unsigned ones through the relation
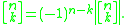
Hence the generating function
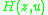of these numbers is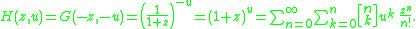A variety of identities may be derived by manipulating this generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
:
In particular, the order of summation may be exchanged, and derivatives taken, and then z or u may be fixed.
Finite sums
A simple sum is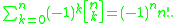This formula holds because the exponential generating function of the sum is
Infinite sums
Some infinite sums include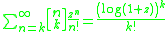where
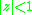(the singularity nearest to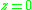 of
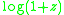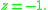is at )This relation holds because
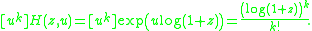
Stirling numbers of the second kind
These numbers count the number of partitions of [n] into k nonempty subsets. First consider the total number of partitions, i.e. Bn where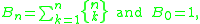i.e. the Bell numbers. The fundamental theorem of combinatorial enumeration
Fundamental theorem of combinatorial enumeration
The fundamental theorem of combinatorial enumeration is a theorem in combinatorics that solves the enumeration problem of labelled and unlabelled combinatorial classes.The unlabelled case is based on the Pólya enumeration theorem....
applies (labelled case).
The set
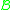of partitions into non-empty subsets is given by ("set of non-empty sets of singletons")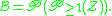This decomposition is entirely analogous to the construction of the set
of permutations from cycles, which is given by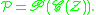and yields the Stirling numbers of the first kind. Hence the name "Stirling numbers of the second kind."
The decomposition is equivalent to the EGF
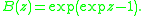
Differentiate to obtain
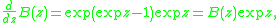
which implies that
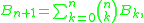
by convolution of exponential generating functions and because differentiating an EGF drops the first coefficient and shifts Bn+1 to z n/n
The EGF of the Stirling numbers of the second kind is obtained by marking every subset that goes into the partition with the term
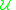, giving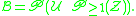Translating to generating functions, we obtain
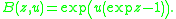
This EGF yields the formula for the Stirling numbers of the second kind:
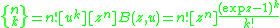
or
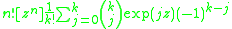
which simplifies to
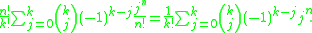
External links
- Philippe Flajolet and Robert Sedgewick, Analytic combinatorics - Symbolic combinatorics.