Fundamental theorem of combinatorial enumeration
Encyclopedia
The fundamental theorem of combinatorial enumeration is a theorem in combinatorics that solves the enumeration problem of labelled and unlabelled combinatorial classes.
The unlabelled case is based on the Pólya enumeration theorem
.
This theorem is also known as the "folklore theorem of enumeration" and its most important application is the creation of symbolic operators, the so-called "symbolic method", that makes it possible to translate equations involving combinatorial structures directly (and automatically) into equations in the generating functions of these structures. For an introduction to the symbolic method, consult the page on symbolic combinatorics
.
The Pólya enumeration theorem
solves this problem in the unlabelled case. Let f(z) be the ordinary generating function (OGF) of the objects, then the OGF of the configurations is given by the substituted cycle index
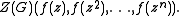
In the labelled case we use an exponential generating function (EGF) g(z) of the objects and apply the Labelled enumeration theorem, which says that the EGF of the configurations is given by
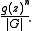
We are able to enumerate filled slot configurations using either PET in the unlabelled case or the labelled enumeration theorem in the labelled case. We now ask about the generating function of configurations obtained when there is more than one set of slots, with a permutation group acting on each. Clearly the orbits do not intersect and we may add the respective generating functions. Suppose, for example, that we want to enumerate unlabelled sequences of length two or three of some objects contained in a set X. There are two sets of slots, the first one containing two slots, and the second one, three slots. The group acting on the first set is
, and on the second slot, 
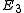. We represent this by the following formal power series in X:
where the term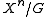
is used to denote the set of orbits under G and 
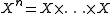, which denotes in the obvious way the process of distributing the objects from X with repetition into the n slots. Similarly, consider the labelled problem of creating cycles of arbitrary length from a set of labelled objects X. This yields the following series of actions of cyclic groups:
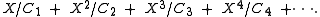
Clearly we can assign meaning to any such power series of quotients (orbits) with respect to permutation groups, where we restrict the groups of degree n to the conjugacy classes
of the symmetric group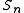 
, which form a unique factorization domain. (The orbits with respect to two groups from the same conjugacy class are isomorphic.) This motivates the following definition.
A class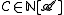
of combinatorial structures is a formal series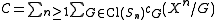
where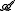
(the "A" is for "atoms") is the set of primes of the UFD 
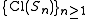and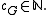 
In the following we will simplify our notation a bit and write e.g.
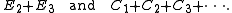
for the classes mentioned above.
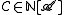be a class of combinatorial structures. The OGF 
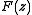of 
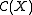where X has OGF 
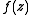and the EGF 
of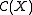 
where X is labelled with EGF 
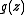are given by
and
In the labelled case we have the additional requirement that X not contain elements of size zero. It will sometimes prove convenient to add one to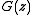
to indicate the presence of one copy of the empty set. It is possible to assign meaning to both 
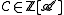(the most common example is the case of unlabelled sets) and 
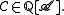To prove the theorem simply apply PET (Pólya enumeration theorem) and the labelled enumeration theorem.
The power of this theorem lies in the fact that it makes it possible to construct operators on generating functions that represent combinatorial classes. A structural equation between combinatorial classes thus translates directly into an equation in the corresponding generating functions. Moreover in the labelled case it is evident from the formula that we may replace
by the atom z and compute the resulting operator, which may then be applied to EGFs. We now proceed to construct the most important operators. The reader may wish to compare with the data on the cycle index
page.
The sequence operator
This operator corresponds to the class
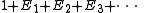
and represents sequences, i.e. the slots are not being permuted and there is exactly one empty sequence. We have
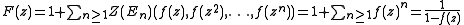
and
The cycle operator
This operator corresponds to the class
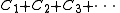
i.e., cycles containing at least one object. We have
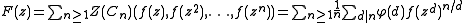
or
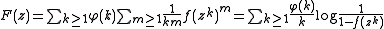
and
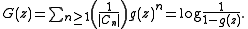
This operator, together with the set operator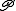
, and their restrictions to specific degrees are used to compute random permutation statistics
. There are two useful restrictions of this operator, namely to even and odd cycles.
The labelled even cycle operator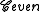
is
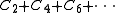
which yields
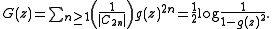
This implies that the labelled odd cycle operator
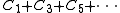
is given by
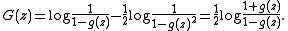
The multiset/set operator
The series is
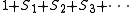
i.e., the symmetric group is applied to the slots. This creates multisets in the unlabelled case and sets in the labelled case (there are no multisets in the labelled case because the labels distinguish multiple instances of the same object from the set being put into different slots). We include the empty set in both the labelled and the unlabelled case.
The unlabelled case is done using the function
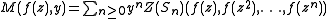
so that
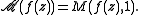
Evaluating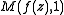
we obtain
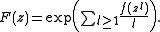
For the labelled case we have
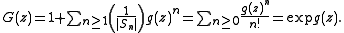
In the labelled case we denote the operator by
, and in the unlabelled case, by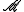 
.
The unlabelled case is based on the Pólya enumeration theorem
Pólya enumeration theorem
The Pólya enumeration theorem , also known as the Redfield–Pólya Theorem, is a theorem in combinatorics that both follows and ultimately generalizes Burnside's lemma on the number of orbits of a group action on a set. The theorem was first published by John Howard Redfield in 1927...
.
This theorem is also known as the "folklore theorem of enumeration" and its most important application is the creation of symbolic operators, the so-called "symbolic method", that makes it possible to translate equations involving combinatorial structures directly (and automatically) into equations in the generating functions of these structures. For an introduction to the symbolic method, consult the page on symbolic combinatorics
Symbolic combinatorics
In mathematics, symbolic combinatorics is one of the many techniques of counting combinatorial objects. It uses the internal structure of the objects to derive formulas for their generating functions. This particular theory is due to Philippe Flajolet and Robert Sedgewick. This article describes...
.
Classes of combinatorial structures
Consider the problem of distributing objects given by a generating function into a set of n slots, where a permutation group G of degree n acts on the slots to create an equivalence relation of filled slot configurations, and asking about the generating function of the configurations by weight of the configurations with respect to this equivalence relation, where the weight of a configuration is the sum of the weights of the objects in the slots. We will first explain how to solve this problem in the labelled and the unlabelled case and use the solution to motivate the creation of classes of combinatorial structures.The Pólya enumeration theorem
Pólya enumeration theorem
The Pólya enumeration theorem , also known as the Redfield–Pólya Theorem, is a theorem in combinatorics that both follows and ultimately generalizes Burnside's lemma on the number of orbits of a group action on a set. The theorem was first published by John Howard Redfield in 1927...
solves this problem in the unlabelled case. Let f(z) be the ordinary generating function (OGF) of the objects, then the OGF of the configurations is given by the substituted cycle index
Cycle index
In mathematics, and in particular in the field of combinatorics, cycle indices are used in combinatorial enumeration when symmetries are to be taken into account...
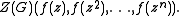
In the labelled case we use an exponential generating function (EGF) g(z) of the objects and apply the Labelled enumeration theorem, which says that the EGF of the configurations is given by
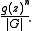
We are able to enumerate filled slot configurations using either PET in the unlabelled case or the labelled enumeration theorem in the labelled case. We now ask about the generating function of configurations obtained when there is more than one set of slots, with a permutation group acting on each. Clearly the orbits do not intersect and we may add the respective generating functions. Suppose, for example, that we want to enumerate unlabelled sequences of length two or three of some objects contained in a set X. There are two sets of slots, the first one containing two slots, and the second one, three slots. The group acting on the first set is
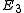, and on the second slot, . We represent this by the following formal power series in X:where the term
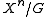is used to denote the set of orbits under G and 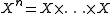, which denotes in the obvious way the process of distributing the objects from X with repetition into the n slots. Similarly, consider the labelled problem of creating cycles of arbitrary length from a set of labelled objects X. This yields the following series of actions of cyclic groups: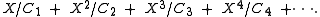Clearly we can assign meaning to any such power series of quotients (orbits) with respect to permutation groups, where we restrict the groups of degree n to the conjugacy classes
of the symmetric group 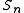, which form a unique factorization domain. (The orbits with respect to two groups from the same conjugacy class are isomorphic.) This motivates the following definition.A class
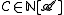of combinatorial structures is a formal series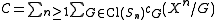where
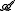(the "A" is for "atoms") is the set of primes of the UF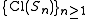D and 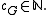In the following we will simplify our notation a bit and write e.g.
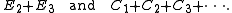
for the classes mentioned above.
The fundamental theorem of combinatorial enumeration
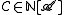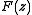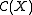Let be a class of combinatorial structures. The OGF of where X has OGF 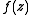and the EGF of 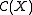where X is labelled with EGF 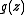are given byand
In the labelled case we have the additional requirement that X not contain elements of size zero. It will sometimes prove convenient to add one to
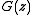to indicate the presence of one copy of the empty set. It is possible to assign meaning to both 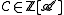(the most common example is the case of unlabelled sets) and 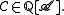To prove the theorem simply apply PET (Pólya enumeration theorem) and the labelled enumeration theorem.The power of this theorem lies in the fact that it makes it possible to construct operators on generating functions that represent combinatorial classes. A structural equation between combinatorial classes thus translates directly into an equation in the corresponding generating functions. Moreover in the labelled case it is evident from the formula that we may replace
by the atom z and compute the resulting operator, which may then be applied to EGFs. We now proceed to construct the most important operators. The reader may wish to compare with the data on the cycle indexCycle index
In mathematics, and in particular in the field of combinatorics, cycle indices are used in combinatorial enumeration when symmetries are to be taken into account...
page.
The sequence operator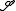 
This operator corresponds to the class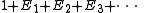and represents sequences, i.e. the slots are not being permuted and there is exactly one empty sequence. We have
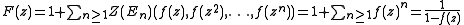
and
The cycle operator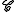 
This operator corresponds to the class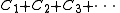i.e., cycles containing at least one object. We have
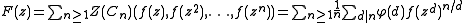
or
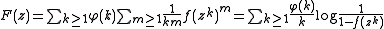
and
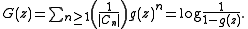
This operator, together with the set operator
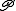, and their restrictions to specific degrees are used to compute random permutation statisticsRandom permutation statistics
The statistics of random permutations, such as the cycle structure of a random permutation are of fundamental importance in the analysis of algorithms, especially of sorting algorithms, which operate on random permutations. Suppose, for example, that we are using quickselect to select a random...
. There are two useful restrictions of this operator, namely to even and odd cycles.
The labelled even cycle operator
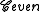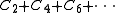
iswhich yields
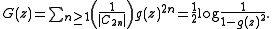
This implies that the labelled odd cycle operator
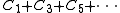
is given by
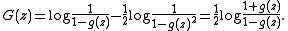
The multiset/set operator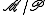 
The series is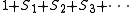i.e., the symmetric group is applied to the slots. This creates multisets in the unlabelled case and sets in the labelled case (there are no multisets in the labelled case because the labels distinguish multiple instances of the same object from the set being put into different slots). We include the empty set in both the labelled and the unlabelled case.
The unlabelled case is done using the function
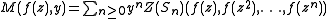
so that
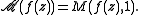
Evaluating
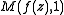we obtain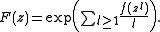For the labelled case we have
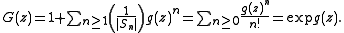
In the labelled case we denote the operator by
, and in the unlabelled case, by 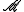.External links
- Philippe Flajolet and Robert Sedgewick, Analytic combinatorics: Symbolic combinatorics.