
Stirling numbers of the second kind
Encyclopedia
In mathematics
, particularly in combinatorics
, a Stirling number of the second kind is the number of ways to partition a set
of n objects into k non-empty subsets and is denoted by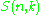 or
or  . Stirling numbers of the second kind occur in the field of mathematics
. Stirling numbers of the second kind occur in the field of mathematics
called combinatorics
and the study of partitions
.
Stirling numbers of the second kind is one of two types of Stirling number
s, the other type being called Stirling numbers of the first kind
. Mutually inverse (finite or infinite) triangular matrices
can be formed by arranging the Stirling numbers of the first respectively second kind according to the parameters n, k.
 count the number of ways to partition a set of n labelled objects into k nonempty unlabelled subsets. Equivalently, they count the number of different equivalence relation
count the number of ways to partition a set of n labelled objects into k nonempty unlabelled subsets. Equivalently, they count the number of different equivalence relation
s with precisely k equivalence classes that can be defined on an n element set. They can be calculated using the following explicit formula:
 was used by Imanuel Marx and Antonio Salmeri in 1962 for variants of these numbers. This led Knuth to use it, as shown here, in the first volume of The Art of Computer Programming
was used by Imanuel Marx and Antonio Salmeri in 1962 for variants of these numbers. This led Knuth to use it, as shown here, in the first volume of The Art of Computer Programming
(1968). However, according to the third edition of The Art of Computer Programming, this notation was also used earlier by Jovan Karamata
in 1935. The notation S(n,k) was used by Richard Stanley
in his book Enumerative Combinatorics
.

the nth Bell number, that is the total number of partitions
of a set with n members.
If we let
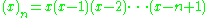
(in particular, (x)0 = 1 because it is an empty product
) be the falling factorial, we can characterize the Stirling numbers of the second kind by
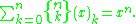
of values for the Stirling numbers of the second kind :
As with the binomial coefficients, this table could be extended to k > n, but those entries would all be 0.
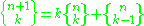
for k > 0 with initial conditions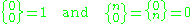
for n > 0.
For instance, the number 25 in column k=3 and row n=5 is given by 25=7+(3×6), where 7 is the number above and to the left of 25, 6 is the number above 25 and 3 is the column containing the 6.
To understand this recurrence, observe that a partition of the n+1 objects into k nonempty subsets either contains the subset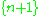 or it does not. The number of ways that
or it does not. The number of ways that  is one of the subsets is given by
is one of the subsets is given by
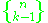
since we must partition the remaining objects into the available
objects into the available 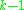 subsets. The number of ways that
subsets. The number of ways that 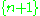 is not one of the subsets (that is, n+1 belongs to a subset containing other elements) is given by
is not one of the subsets (that is, n+1 belongs to a subset containing other elements) is given by
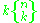
since we partition all elements other than n+1 into k subsets, and then are left with k choices for inserting the element n+1. Summing these two values gives the desired result.
:
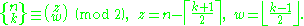
This relation is specified by mapping n and k coordinates onto the Sierpiński triangle
.
Or directly, let two sets contain positions of 1's in binary representations of results of respective expressions:
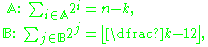
then mimic a bitwise AND operation by intersecting these two sets:

to obtain the parity of a Stirling number of the second kind in O(1)
time. In pseudocode
:
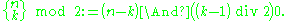
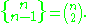
This is because dividing n elements into n − 1 sets necessarily means dividing it into one set of size 2 and n − 2 sets of size 1. Therefore we need only pick those two elements;
and
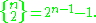
To see this, first note that there are 2 n ordered pairs of complementary subsets A and B. In one case, A is empty, and in another B is empty, so 2 n − 2 ordered pairs of subsets remain. Finally, since we want unordered pairs rather than ordered pairs we divide this last number by 2, giving the result above.
Another explicit expanding of the recurrence-relation gives identities in the spirit of the above example.
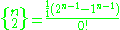
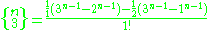
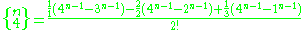
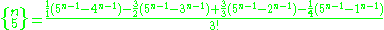
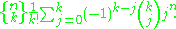
This formula is a special case of the k 'th forward difference of the monomial
 evaluated at x = 0:
evaluated at x = 0:
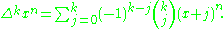
Because the Bernoulli polynomials may be written in terms of these forward differences, one immediately obtains a relation in the Bernoulli number
s:
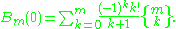
for the Stirling numbers of the second kind is given by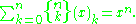
with a Poisson distribution
with expected value
λ, then its nth moment
is
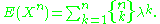
In particular, the nth moment of the Poisson distribution with expected value 1 is precisely the number of partitions of a set
of size n, i.e., it is the nth Bell number (this fact is Dobinski's formula).
of a finite set of size m. Then the nth moment of X is
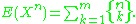
Note: The upper bound of summation is m, not n.
In other words, the nth moment of this probability distribution
is the number of partitions of a set of size n into no more than m parts.
This is proved on the page on random permutation statistics, although the notation is a bit different.
s for a poem of n lines.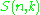 gives the number of possible rhyming schemes for n lines using k unique rhyming syllables. As an example, for a poem of 3 lines, there is 1 rhyme scheme using just one rhyme (aaa), 3 rhyme schemes using two rhymes (aab, aba, abb), and 1 rhyme scheme using three rhymes (abc).
gives the number of possible rhyming schemes for n lines using k unique rhyming syllables. As an example, for a poem of 3 lines, there is 1 rhyme scheme using just one rhyme (aaa), 3 rhyme schemes using two rhymes (aab, aba, abb), and 1 rhyme scheme using three rhymes (abc).
Reduced Stirling numbers of the second kind
Denote the n objects to partition by the integers 1, 2, ..., n. Define the reduced Stirling numbers of the second kind, denoted , to be the number of ways to partition the integers 1, 2, ..., n into k nonempty subsets such that all elements in each subset have pairwise distance at least d. That is, for any integers i and j in a given subset, it is required that
, to be the number of ways to partition the integers 1, 2, ..., n into k nonempty subsets such that all elements in each subset have pairwise distance at least d. That is, for any integers i and j in a given subset, it is required that 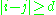 . It has been shown that these numbers satisfy
. It has been shown that these numbers satisfy
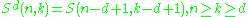
(hence the name "reduced"). Observe (both by definition and by the reduction formula), that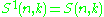 , the familiar Stirling numbers of the second kind.
, the familiar Stirling numbers of the second kind.
See also
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, a Stirling number of the second kind is the number of ways to partition a set
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of n objects into k non-empty subsets and is denoted by
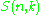 or
or 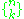 . Stirling numbers of the second kind occur in the field of mathematics
. Stirling numbers of the second kind occur in the field of mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
called combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and the study of partitions
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
.
Stirling numbers of the second kind is one of two types of Stirling number
Stirling number
In mathematics, Stirling numbers arise in a variety of combinatorics problems. They are named after James Stirling, who introduced them in the 18th century. Two different sets of numbers bear this name: the Stirling numbers of the first kind and the Stirling numbers of the second...
s, the other type being called Stirling numbers of the first kind
Stirling numbers of the first kind
In mathematics, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling numbers. They commonly occur in combinatorics, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be...
. Mutually inverse (finite or infinite) triangular matrices
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
can be formed by arranging the Stirling numbers of the first respectively second kind according to the parameters n, k.
Definition
The Stirling numbers of the second kind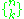 count the number of ways to partition a set of n labelled objects into k nonempty unlabelled subsets. Equivalently, they count the number of different equivalence relation
count the number of ways to partition a set of n labelled objects into k nonempty unlabelled subsets. Equivalently, they count the number of different equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s with precisely k equivalence classes that can be defined on an n element set. They can be calculated using the following explicit formula:

Notation
Various notations have been used for Stirling numbers of the second kind. The brace notation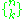 was used by Imanuel Marx and Antonio Salmeri in 1962 for variants of these numbers. This led Knuth to use it, as shown here, in the first volume of The Art of Computer Programming
was used by Imanuel Marx and Antonio Salmeri in 1962 for variants of these numbers. This led Knuth to use it, as shown here, in the first volume of The Art of Computer ProgrammingThe Art of Computer Programming
The Art of Computer Programming is a comprehensive monograph written by Donald Knuth that covers many kinds of programming algorithms and their analysis....
(1968). However, according to the third edition of The Art of Computer Programming, this notation was also used earlier by Jovan Karamata
Jovan Karamata
Jovan Karamata was one of the greatest Serbian mathematicians of the 20th century. He is remembered for contributions to analysis, in particular, the Tauberian theory and the theory of slowly varying functions...
in 1935. The notation S(n,k) was used by Richard Stanley
Richard P. Stanley
Richard Peter Stanley is the Norman Levinson Professor of Applied Mathematics at the Massachusetts Institute of Technology, in Cambridge, Massachusetts. He received his Ph.D. at Harvard University in 1971 under the supervision of Gian-Carlo Rota...
in his book Enumerative Combinatorics
Enumerative combinatorics
Enumerative combinatorics is an area of combinatorics that deals with the number of ways that certain patterns can be formed. Two examples of this type of problem are counting combinations and counting permutations...
.
Bell numbers
The sum over the values for k of the Stirling numbers of the second kind, gives us
the nth Bell number, that is the total number of partitions
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of a set with n members.
If we let
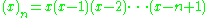
(in particular, (x)0 = 1 because it is an empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
) be the falling factorial, we can characterize the Stirling numbers of the second kind by
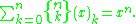
Table of values
Below is a triangular arrayTriangular array
In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index.Notable particular examples include these:...
of values for the Stirling numbers of the second kind :
| n \ k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 1 | ||||||||||
| 1 | 0 | 1 | |||||||||
| 2 | 0 | 1 | 1 | ||||||||
| 3 | 0 | 1 | 3 | 1 | |||||||
| 4 | 0 | 1 | 7 | 6 | 1 | ||||||
| 5 | 0 | 1 | 15 | 25 | 10 | 1 | |||||
| 6 | 0 | 1 | 31 | 90 | 65 | 15 | 1 | ||||
| 7 | 0 | 1 | 63 | 301 | 350 | 140 | 21 | 1 | |||
| 8 | 0 | 1 | 127 | 966 | 1701 | 1050 | 266 | 28 | 1 | ||
| 9 | 0 | 1 | 255 | 3025 | 7770 | 6951 | 2646 | 462 | 36 | 1 | |
| 10 | 0 | 1 | 511 | 9330 | 34105 | 42525 | 22827 | 5880 | 750 | 45 | 1 |
As with the binomial coefficients, this table could be extended to k > n, but those entries would all be 0.
Recurrence relation
Stirling numbers of the second kind obey the recurrence relation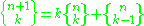
for k > 0 with initial conditions
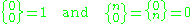
for n > 0.
For instance, the number 25 in column k=3 and row n=5 is given by 25=7+(3×6), where 7 is the number above and to the left of 25, 6 is the number above 25 and 3 is the column containing the 6.
To understand this recurrence, observe that a partition of the n+1 objects into k nonempty subsets either contains the subset
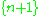 or it does not. The number of ways that
or it does not. The number of ways that  is one of the subsets is given by
is one of the subsets is given by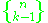
since we must partition the remaining
 objects into the available
objects into the available 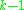 subsets. The number of ways that
subsets. The number of ways that 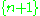 is not one of the subsets (that is, n+1 belongs to a subset containing other elements) is given by
is not one of the subsets (that is, n+1 belongs to a subset containing other elements) is given by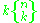
since we partition all elements other than n+1 into k subsets, and then are left with k choices for inserting the element n+1. Summing these two values gives the desired result.
Parity
The parity of a Stirling number of the second kind is equal to the parity of a related binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
:
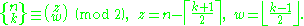
This relation is specified by mapping n and k coordinates onto the Sierpiński triangle
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
.
Or directly, let two sets contain positions of 1's in binary representations of results of respective expressions:
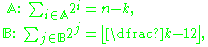
then mimic a bitwise AND operation by intersecting these two sets:

to obtain the parity of a Stirling number of the second kind in O(1)
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
time. In pseudocode
Pseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
:
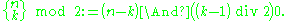
Simple identities
Some simple identities include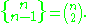
This is because dividing n elements into n − 1 sets necessarily means dividing it into one set of size 2 and n − 2 sets of size 1. Therefore we need only pick those two elements;
and
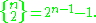
To see this, first note that there are 2 n ordered pairs of complementary subsets A and B. In one case, A is empty, and in another B is empty, so 2 n − 2 ordered pairs of subsets remain. Finally, since we want unordered pairs rather than ordered pairs we divide this last number by 2, giving the result above.
Another explicit expanding of the recurrence-relation gives identities in the spirit of the above example.
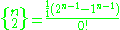
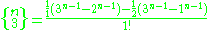
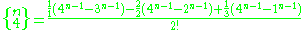
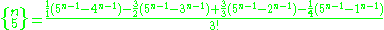
Explicit formula
The Stirling numbers of the second kind are given by the explicit formula: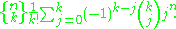
This formula is a special case of the k 'th forward difference of the monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
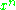 evaluated at x = 0:
evaluated at x = 0: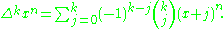
Because the Bernoulli polynomials may be written in terms of these forward differences, one immediately obtains a relation in the Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s:
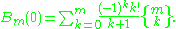
Generating function
A generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the Stirling numbers of the second kind is given by
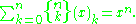
Moments of the Poisson distribution
If X is a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
λ, then its nth moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
is
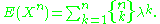
In particular, the nth moment of the Poisson distribution with expected value 1 is precisely the number of partitions of a set
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of size n, i.e., it is the nth Bell number (this fact is Dobinski's formula).
Moments of fixed points of random permutations
Let the random variable X be the number of fixed points of a uniformly distributed random permutationRandom permutation
A random permutation is a random ordering of a set of objects, that is, a permutation-valued random variable. The use of random permutations is often fundamental to fields that use randomized algorithms such as coding theory, cryptography, and simulation...
of a finite set of size m. Then the nth moment of X is
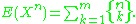
Note: The upper bound of summation is m, not n.
In other words, the nth moment of this probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is the number of partitions of a set of size n into no more than m parts.
This is proved on the page on random permutation statistics, although the notation is a bit different.
Rhyming schemes
The Stirling numbers of the second kind can represent the total number of rhyme schemeRhyme scheme
A rhyme scheme is the pattern of rhyme between lines of a poem or song. It is usually referred to by using letters to indicate which lines rhyme. In other words, it is the pattern of end rhymes or lines...
s for a poem of n lines.
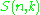 gives the number of possible rhyming schemes for n lines using k unique rhyming syllables. As an example, for a poem of 3 lines, there is 1 rhyme scheme using just one rhyme (aaa), 3 rhyme schemes using two rhymes (aab, aba, abb), and 1 rhyme scheme using three rhymes (abc).
gives the number of possible rhyming schemes for n lines using k unique rhyming syllables. As an example, for a poem of 3 lines, there is 1 rhyme scheme using just one rhyme (aaa), 3 rhyme schemes using two rhymes (aab, aba, abb), and 1 rhyme scheme using three rhymes (abc).Reduced Stirling numbers of the second kind
Denote the n objects to partition by the integers 1, 2, ..., n. Define the reduced Stirling numbers of the second kind, denoted
 , to be the number of ways to partition the integers 1, 2, ..., n into k nonempty subsets such that all elements in each subset have pairwise distance at least d. That is, for any integers i and j in a given subset, it is required that
, to be the number of ways to partition the integers 1, 2, ..., n into k nonempty subsets such that all elements in each subset have pairwise distance at least d. That is, for any integers i and j in a given subset, it is required that 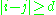 . It has been shown that these numbers satisfy
. It has been shown that these numbers satisfy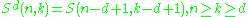
(hence the name "reduced"). Observe (both by definition and by the reduction formula), that
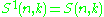 , the familiar Stirling numbers of the second kind.
, the familiar Stirling numbers of the second kind.See also
- Bell numberBell numberIn combinatorics, the nth Bell number, named after Eric Temple Bell, is the number of partitions of a set with n members, or equivalently, the number of equivalence relations on it...
– the number of partitions of a set with n members - Stirling numbers of the first kindStirling numbers of the first kindIn mathematics, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling numbers. They commonly occur in combinatorics, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be...


