
Random permutation
Encyclopedia
A random permutation is a random ordering of a set of objects, that is, a permutation
-valued random variable
. The use of random permutations is often fundamental to fields that use randomized algorithm
s such as coding theory
, cryptography
, and simulation
. A good example of a random permutation is the shuffling of a deck of cards: this is ideally a random permutation of the 52 cards.
s is equally likely to appear) is to generate a sequence by taking a random number between 1 and n sequentially, ensuring that there is no repetition, and interpreting this sequence {x1, ..., xn} as the permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
-valued random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
. The use of random permutations is often fundamental to fields that use randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
s such as coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, and simulation
Simulation
Simulation is the imitation of some real thing available, state of affairs, or process. The act of simulating something generally entails representing certain key characteristics or behaviours of a selected physical or abstract system....
. A good example of a random permutation is the shuffling of a deck of cards: this is ideally a random permutation of the 52 cards.
Entry-by-entry brute force
One method of generating a random permutation of a set of length n uniformly at random (i.e., each of the n! permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s is equally likely to appear) is to generate a sequence by taking a random number between 1 and n sequentially, ensuring that there is no repetition, and interpreting this sequence {x1, ..., xn} as the permutation
-
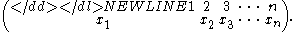
The above brute-force method will require occasional retries whenever the random number picked is a repeat of a number already selected. This can be avoided if, on the ith step (when x1, ..., xi − 1 have already been chosen), one chooses a number j at random between 1 and n − i + 1 and sets xi equal to the jth largest of the unchosen numbers.
Knuth shuffles
A simple algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to generate a permutation of n items uniformly at random without retries, known as the Knuth shuffle, is to start with any permutation (for example, the identity permutationIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
), and then go through the positions 1 through n − 1, and for each position i swap the element currently there with an arbitrarily chosen element from positions i through n, inclusive. It's easy to verify that any permutation of n elements will be produced by this algorithm with probability exactly 1/n!, thus yielding a uniform distribution over all such permutations.
Fixed points
The probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the number of fixed pointsFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of a uniformly distributed random permutation approaches a Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
1 as n grows. In particular, it is an elegant application of the inclusion-exclusion principleInclusion-exclusion principleIn combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
to show that the probability that there are no fixed points approaches 1/e. The first n momentsMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of this distribution are exactly those of the Poisson distribution.
Randomness testing
As with all random processes, the quality of the resulting distribution of an implementation of a randomized algorithm such as the Knuth shuffle (i.e., how close it is to the desired uniform distribution) depends on the quality of the underlying source of randomness, such as a pseudorandom number generatorPseudorandom number generatorA pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
. There are many possible randomness tests for random permutations, such as some of the Diehard testsDiehard testsThe diehard tests are a battery of statistical tests for measuring the quality of a random number generator. They were developed by George Marsaglia over several years and first published in 1995 on a CD-ROM of random numbers.These are the tests:...
. A typical example of such a test is to take some permutation statistic for which the distribution is known and test whether the distribution of this statistic on a set of randomly generated permutations closely approximates the true distribution.
See also
- Ewens's sampling formulaEwens's sampling formulaIn population genetics, Ewens' sampling formula, describes the probabilities associated with counts of how many different alleles are observed a given number of times in the sample.-Definition:...
— a connection with population geneticsPopulation geneticsPopulation genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population... - Golomb–Dickman constant
- Perfect shuffle
- Random permutation statisticsRandom permutation statisticsThe statistics of random permutations, such as the cycle structure of a random permutation are of fundamental importance in the analysis of algorithms, especially of sorting algorithms, which operate on random permutations. Suppose, for example, that we are using quickselect to select a random...
- Shuffling algorithms — random sort method, iterative exchange method
External links
- Random permutation at MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Random permutation generation -- detailed and practical explanation of Knuth shuffle algorithm and its variants for generating k-permutations (permutations of k elements chosen from a list) and k-subsets (generating a subset of the elements in the list without replacement) with pseudocode
- Ewens's sampling formula

