Polynomial expansion
Encyclopedia
In mathematics
, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition. Expansion of a polynomial expression
can be obtained by repeatedly replacing subexpressions that multiply two other subexpressions, at least one of which is an addition, by the equivalent sum of products, continuing until the expression becomes a sum of (repeated) products. During the expansion, simplifications such are grouping of like terms or cancellations of terms may also be applied. Instead of multiplications, the expansion steps could also involve replacing powers of a sum of terms by the equivalent expression obtained from the binomial formula; this is a shortened form of what would happen if the power were treated as a repeated multiplication, and expanded repeatedly. It is customary to reintroduce powers in the final result when terms involve products of identical symbols.
Simple examples of polynomial expansions are the well known rules
when used from left to right. A more general single-step expansion will introduce all products of a term of one of the sums being multiplied with a term of the other:
An expansion which involves multiple nested rewrite steps is that of working out a Horner scheme
to the (expanded) polynomial it defines, for instance
.
The opposite process of trying to write an expanded polynomial as a product is called polynomial factorization
.
s, the FOIL rule
can be used, which stands for "First Outer Inner Last," referring to the terms that are multiplied together. For example, expanding
yields
When expanding
, a special relationship exists between the coefficients of the terms when written in order of descending powers of x and ascending powers of y. The coefficients will be the numbers in the (n + 1)th row of Pascal's triangle
.
For example, when expanding
, the following is obtained: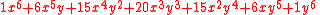
Online tools
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition. Expansion of a polynomial expression
Polynomial expression
In mathematics, and in particular in the field of algebra, a polynomial expression in one or more given entities E1, E2, ..., is any meaningful expression constructed from copies of those entities together with constants, using the operations of addition and multiplication...
can be obtained by repeatedly replacing subexpressions that multiply two other subexpressions, at least one of which is an addition, by the equivalent sum of products, continuing until the expression becomes a sum of (repeated) products. During the expansion, simplifications such are grouping of like terms or cancellations of terms may also be applied. Instead of multiplications, the expansion steps could also involve replacing powers of a sum of terms by the equivalent expression obtained from the binomial formula; this is a shortened form of what would happen if the power were treated as a repeated multiplication, and expanded repeatedly. It is customary to reintroduce powers in the final result when terms involve products of identical symbols.
Simple examples of polynomial expansions are the well known rules
when used from left to right. A more general single-step expansion will introduce all products of a term of one of the sums being multiplied with a term of the other:
An expansion which involves multiple nested rewrite steps is that of working out a Horner scheme
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
to the (expanded) polynomial it defines, for instance
.The opposite process of trying to write an expanded polynomial as a product is called polynomial factorization
Polynomial factorization
In mathematics and computer algebra, polynomial factorization refers to factoring a polynomial into irreducible polynomials over a given field.-Formulation of the question:...
.
Expansion of a polynomial written in factored form
To multiply two factors, each term of the first factor must be multiplied by each term of the other factor. If both factors are binomialBinomial
In algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...
s, the FOIL rule
FOIL rule
In elementary algebra, FOIL is a mnemonic for the standard method of multiplying two binomials—hence the method may be referred to as the FOIL method...
can be used, which stands for "First Outer Inner Last," referring to the terms that are multiplied together. For example, expanding
yields
Expansion of (x+y)n
When expanding
, a special relationship exists between the coefficients of the terms when written in order of descending powers of x and ascending powers of y. The coefficients will be the numbers in the (n + 1)th row of Pascal's trianglePascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
.
For example, when expanding
, the following is obtained: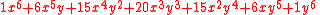External links
Discussion- Review of Algebra: Expansion, University of AkronUniversity of AkronThe University of Akron is a coeducational public research university located in Akron, Ohio, United States. The university is part of the University System of Ohio. It was founded in 1870 as a small college affiliated with the Universalist Church. In 1913 ownership was transferred to the City of...
Online tools
- Expand page, quickmath.com
- Online Calculator with Symbolic Calculations, livephysics.com