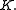Polynomial factorization
Encyclopedia
In mathematics
and computer algebra, polynomial factorization refers to factoring a polynomial into irreducible polynomial
s over a given field
.
factorization exist, but the irreducible factorization, the most common, is the subject of this article.
Factorization depends strongly on the choice of field. For example, the fundamental theorem of algebra
, which states that all polynomials with complex
coefficients have complex roots, implies that a polynomial with integer
coefficient
s can be completely reduced to linear factor
s over the complex field C.
On the other hand, such a polynomial may only be reducible to linear and quadratic
factors over the real
field R. Over the rational number
field Q, it is possible that no factorization at all may be possible. From a more practical vantage point, the fundamental theorem is only an existence proof, and offers little insight into the common problem of actually finding the roots of a given polynomial.
can be reduced to factoring over the corresponding integral domain. This algebraic point goes by the name of Gauss's lemma
.
The classic proof, due to Gauss
, first factors a polynomial into its content, a rational number, and its primitive part, a polynomial whose coefficients are pure integers and share no common divisor among them. Any polynomial with rational coefficients can be factored in this way, using a content composed of the greatest common divisor of the numerators, and the least common multiple of the denominators. This factorization is unique.
For example,
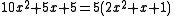
and
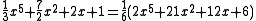
since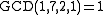 and
and 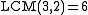 .
.
Now, any polynomial with rational coefficients can be split into a content and a primitive polynomial, and in particular the factors of any factorization (over Q) of such a polynomial can also be so split. Since the content and the primitive polynomials are unique, and since the product of primitive polynomials is itself primitive, the primitive part of the polynomial must factor into the primitive parts of the factors. In particular, if a polynomial with integer coefficients can be factored at all, it can be factored into integer polynomials. So factoring a polynomial with rational coefficients can be reduced to finding integer factorizations of its primitive part.
For example, consider
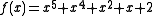 .
.
If this polynomial factors over Z, then at least one of its factors must be of degree two or less. We need three values to uniquely fit a second degree polynomial. We'll use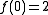 ,
, 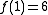 and
and 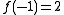 . Now, 2 can only factor as
. Now, 2 can only factor as
Therefore, if a second degree integer polynomial factor exists, it must take one of the values
at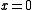 , and likewise at
, and likewise at 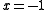 . There are eight different ways to factor 6, so there are
. There are eight different ways to factor 6, so there are
possible combinations, of which half can be discarded as the negatives of the other half, corresponding to 64 possible second degree integer polynomials which must be checked. These are the only possible integer polynomial factors of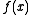 . Testing them exhaustively reveals that
. Testing them exhaustively reveals that
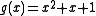
constructed from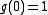 ,
, 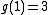 and
and 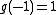 , factors
, factors 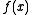 .
.
(Van der Waerden, Sections 5.4 and 5.6)
Lenstra–Lenstra–Lovász lattice basis reduction algorithm
.
One variation of their algorithm runs as follows: calculate a complex (or p-adic) root α of the polynomial P to high precision, then use the Lenstra–Lenstra–Lovász lattice basis reduction algorithm
to find an approximate linear relation between 1, α, α2, α3, ... with integer coefficients, which with luck will be an exact linear relation and a polynomial factor of P.
, and Cantor–Zassenhaus algorithm.
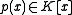 , where
, where 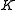 is a finite field extension of
is a finite field extension of 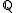 . First we eliminate any repeated factors in
. First we eliminate any repeated factors in 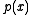 by taking greatest common divisors with its derivative. Next we write
by taking greatest common divisors with its derivative. Next we write 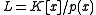 explicitly as an algebra over
explicitly as an algebra over 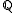 . We next pick a random element
. We next pick a random element 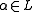 . By the primitive element theorem,
. By the primitive element theorem,  generates
generates 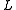 over
over 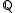 with high probability. If this is the case, we can compute the minimal polynomial,
with high probability. If this is the case, we can compute the minimal polynomial, 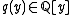 of
of  over
over 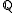 . Factoring
. Factoring
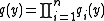
over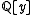 , we determine that
, we determine that
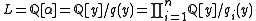
(notice that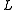 is reduced since
is reduced since 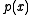 is), where
is), where  corresponds to the element
corresponds to the element 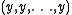 . Note that this is the unique decomposition of
. Note that this is the unique decomposition of 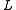 as a product fields. Hence this decomposition is the same as
as a product fields. Hence this decomposition is the same as
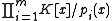
where
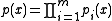
is the factorization of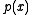 over
over 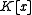 . By writing
. By writing 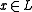 and generators of
and generators of 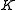 as a polynomials in
as a polynomials in  , we can determine the embeddings of
, we can determine the embeddings of  and
and 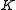 into the components
into the components 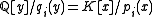 . By finding the minimal polynomial of
. By finding the minimal polynomial of  in this ring, we have computed
in this ring, we have computed 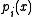 , and thus factored
, and thus factored 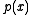 over
over 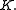
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer algebra, polynomial factorization refers to factoring a polynomial into irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
s over a given field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
Formulation of the question
Other factorizations, such as square-freeSquare-free polynomial
In mathematics, a square-free polynomial is a polynomial with no square factors, i.e, f \in F[x] is square-free if and only if b^2 \nmid f for every b \in F[x] with non-zero degree. This definition implies that no factors of higher order can exist, either, for if b3 divided the polynomial, then b2...
factorization exist, but the irreducible factorization, the most common, is the subject of this article.
Factorization depends strongly on the choice of field. For example, the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
, which states that all polynomials with complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
coefficients have complex roots, implies that a polynomial with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s can be completely reduced to linear factor
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
s over the complex field C.
On the other hand, such a polynomial may only be reducible to linear and quadratic
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
factors over the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
field R. Over the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
field Q, it is possible that no factorization at all may be possible. From a more practical vantage point, the fundamental theorem is only an existence proof, and offers little insight into the common problem of actually finding the roots of a given polynomial.
Factoring over the integers and rationals
It can be shown that factoring over Q (the rational numbers) can be reduced to factoring over Z (the integers). This is a specific example of a more general case — factoring over a field of fractionsField of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
can be reduced to factoring over the corresponding integral domain. This algebraic point goes by the name of Gauss's lemma
Gauss's lemma (polynomial)
In algebra, in the theory of polynomials , Gauss's lemma is either of two related statements about polynomials with integer coefficients:...
.
The classic proof, due to Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, first factors a polynomial into its content, a rational number, and its primitive part, a polynomial whose coefficients are pure integers and share no common divisor among them. Any polynomial with rational coefficients can be factored in this way, using a content composed of the greatest common divisor of the numerators, and the least common multiple of the denominators. This factorization is unique.
For example,
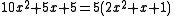
and
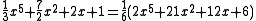
since
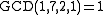 and
and 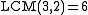 .
.Now, any polynomial with rational coefficients can be split into a content and a primitive polynomial, and in particular the factors of any factorization (over Q) of such a polynomial can also be so split. Since the content and the primitive polynomials are unique, and since the product of primitive polynomials is itself primitive, the primitive part of the polynomial must factor into the primitive parts of the factors. In particular, if a polynomial with integer coefficients can be factored at all, it can be factored into integer polynomials. So factoring a polynomial with rational coefficients can be reduced to finding integer factorizations of its primitive part.
Kronecker's method
Since integer polynomials must factor into integer polynomial factors, and evaluating integer polynomials at integer values must produce integers, the integer values of a polynomial can be factored in only a finite number of ways, and produce only a finite number of possible polynomial factors.For example, consider
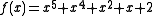 .
.If this polynomial factors over Z, then at least one of its factors must be of degree two or less. We need three values to uniquely fit a second degree polynomial. We'll use
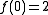 ,
, 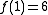 and
and 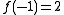 . Now, 2 can only factor as
. Now, 2 can only factor as- 1×2, 2×1, (−1)×(−2), or (−2)×(−1).
Therefore, if a second degree integer polynomial factor exists, it must take one of the values
- 1, 2, −1, or −2
at
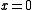 , and likewise at
, and likewise at 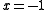 . There are eight different ways to factor 6, so there are
. There are eight different ways to factor 6, so there are- 4×4×8 = 128
possible combinations, of which half can be discarded as the negatives of the other half, corresponding to 64 possible second degree integer polynomials which must be checked. These are the only possible integer polynomial factors of
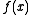 . Testing them exhaustively reveals that
. Testing them exhaustively reveals that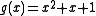
constructed from
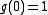 ,
, 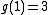 and
and 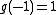 , factors
, factors 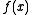 .
.(Van der Waerden, Sections 5.4 and 5.6)
LLL algorithm
The LLL algorithm , was the first polynomial time algorithm for factoring rational polynomials, and uses theLenstra–Lenstra–Lovász lattice basis reduction algorithm
Lenstra–Lenstra–Lovász lattice basis reduction algorithm
The LLL-reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and László Lovász in 1982, see...
.
One variation of their algorithm runs as follows: calculate a complex (or p-adic) root α of the polynomial P to high precision, then use the Lenstra–Lenstra–Lovász lattice basis reduction algorithm
Lenstra–Lenstra–Lovász lattice basis reduction algorithm
The LLL-reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and László Lovász in 1982, see...
to find an approximate linear relation between 1, α, α2, α3, ... with integer coefficients, which with luck will be an exact linear relation and a polynomial factor of P.
Factoring over finite fields
See Factorization of polynomial over finite field and irreducibility tests, Berlekamp's algorithmBerlekamp's algorithm
In mathematics, particularly computational algebra, Berlekamp's algorithm is a well-known method for factoring polynomials over finite fields . The algorithm consists mainly of matrix reduction and polynomial GCD computations. It was invented by Elwyn Berlekamp in 1967...
, and Cantor–Zassenhaus algorithm.
Factoring over algebraic extensions
We can factor a polynomial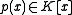 , where
, where 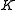 is a finite field extension of
is a finite field extension of 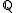 . First we eliminate any repeated factors in
. First we eliminate any repeated factors in 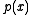 by taking greatest common divisors with its derivative. Next we write
by taking greatest common divisors with its derivative. Next we write 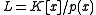 explicitly as an algebra over
explicitly as an algebra over 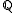 . We next pick a random element
. We next pick a random element 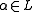 . By the primitive element theorem,
. By the primitive element theorem,  generates
generates 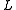 over
over 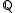 with high probability. If this is the case, we can compute the minimal polynomial,
with high probability. If this is the case, we can compute the minimal polynomial, 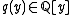 of
of  over
over 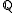 . Factoring
. Factoring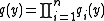
over
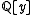 , we determine that
, we determine that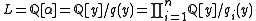
(notice that
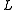 is reduced since
is reduced since 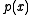 is), where
is), where  corresponds to the element
corresponds to the element 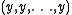 . Note that this is the unique decomposition of
. Note that this is the unique decomposition of 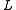 as a product fields. Hence this decomposition is the same as
as a product fields. Hence this decomposition is the same as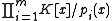
where
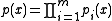
is the factorization of
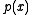 over
over 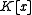 . By writing
. By writing 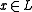 and generators of
and generators of 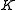 as a polynomials in
as a polynomials in  , we can determine the embeddings of
, we can determine the embeddings of  and
and 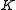 into the components
into the components 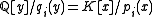 . By finding the minimal polynomial of
. By finding the minimal polynomial of  in this ring, we have computed
in this ring, we have computed 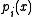 , and thus factored
, and thus factored 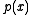 over
over