Square-free polynomial
Encyclopedia
In mathematics
, a square-free polynomial is a polynomial
with no square factors, i.e,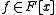
is square-free if and only if 
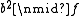for every 
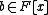with non-zero degree. This definition implies that no factors of higher order can exist, either, for if b3 divided the polynomial, then b2 would divide it also. In applications in physics and engineering, a square-free polynomial is much more commonly called a polynomial with no repeated roots.
Any square factor of a polynomial introduces a nontrivial common factor of f and its formal derivative f ′, so a necessary condition for f to be square-free is that the greatest common divisor
of f and f ′ is 1. If the field F is perfect
, then all irreducible polynomials over F are separable polynomial
s, and so if f is a square-free polynomial over a perfect field, then the condition that f and f ′ are coprime
is also sufficient for f to be square-free.
A square-free factorization of a polynomial is a factorization into powers of square-free factors, i.e:
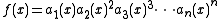
where the ak(x) are pairwise coprime
square-free polynomials. Clearly, any non-zero polynomial admits a square-free factorization, since it can be factored
into irreducible
factors and the multiplicity
of each irreducible factor counted to determine which ak(x) it is part of.
The utility of a square-free factorization is that it is generally easier to compute than a full irreducible factorization. For this reason, square-free factorization is often used as the first step in polynomial factorization or root-finding algorithms. It is also useful in the integration of rational functions via partial fractions (a method due to Hermite).
Over fields of characteristic
0, only differentiation, polynomial division, and GCD
calculation (which can be done using the Euclidean algorithm
) is required to compute the square-free factorization. Let f be a non-zero polynomial, decomposed into square-free factors as above. Consider any irreducible factor q of ƒ: we may write ƒ = qkh, where k > 0 and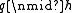
. By the product rule,
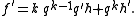
As the characteristic is 0, q does not divide k, q′, or h, thus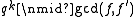
and 
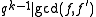. That is, the multiplicity of any irreducible factor in 
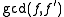is one less than its multiplicity in f, so
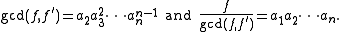
Now, if we compute recursively
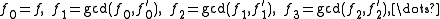
we obtain the polynomials
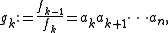
from which we recover the square-free factors as ak = gk/gk+1.
A modification of this algorithm also works for polynomials over finite fields, or more generally, perfect fields of non-zero characteristic p, if we know an algorithm to compute p-th roots of elements of the field.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a square-free polynomial is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with no square factors, i.e,
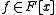is square-free if and only if 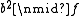for every 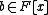with non-zero degree. This definition implies that no factors of higher order can exist, either, for if b3 divided the polynomial, then b2 would divide it also. In applications in physics and engineering, a square-free polynomial is much more commonly called a polynomial with no repeated roots.Any square factor of a polynomial introduces a nontrivial common factor of f and its formal derivative f ′, so a necessary condition for f to be square-free is that the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of f and f ′ is 1. If the field F is perfect
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
, then all irreducible polynomials over F are separable polynomial
Separable polynomial
In mathematics, two slightly different notions of separable polynomial are used, by different authors.According to the most common one, a polynomial P over a given field K is separable if all its roots are distinct in an algebraic closure of K, that is the number of its distinct roots is equal to...
s, and so if f is a square-free polynomial over a perfect field, then the condition that f and f ′ are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
is also sufficient for f to be square-free.
A square-free factorization of a polynomial is a factorization into powers of square-free factors, i.e:
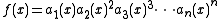
where the ak(x) are pairwise coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
square-free polynomials. Clearly, any non-zero polynomial admits a square-free factorization, since it can be factored
Polynomial factorization
In mathematics and computer algebra, polynomial factorization refers to factoring a polynomial into irreducible polynomials over a given field.-Formulation of the question:...
into irreducible
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
factors and the multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
of each irreducible factor counted to determine which ak(x) it is part of.
The utility of a square-free factorization is that it is generally easier to compute than a full irreducible factorization. For this reason, square-free factorization is often used as the first step in polynomial factorization or root-finding algorithms. It is also useful in the integration of rational functions via partial fractions (a method due to Hermite).
Over fields of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0, only differentiation, polynomial division, and GCD
Greatest common divisor of two polynomials
Informally, the greatest common divisor of two polynomials p and q is the largest polynomial that divides both p and q evenly. The definition is modeled on the concept of the greatest common divisor of two integers, the greatest integer that divides both...
calculation (which can be done using the Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
) is required to compute the square-free factorization. Let f be a non-zero polynomial, decomposed into square-free factors as above. Consider any irreducible factor q of ƒ: we may write ƒ = qkh, where k > 0 and
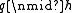. By the product rule,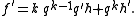As the characteristic is 0, q does not divide k, q′, or h, thus
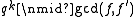and 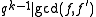. That is, the multiplicity of any irreducible factor in 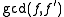is one less than its multiplicity in f, so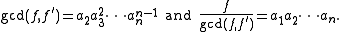Now, if we compute recursively
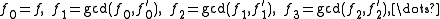
we obtain the polynomials
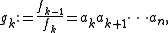
from which we recover the square-free factors as ak = gk/gk+1.
A modification of this algorithm also works for polynomials over finite fields, or more generally, perfect fields of non-zero characteristic p, if we know an algorithm to compute p-th roots of elements of the field.