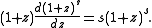Table of Newtonian series
Encyclopedia
In mathematics
, a Newtonian series, named after Isaac Newton
, is a sum over a sequence
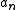written in the form
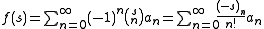
where
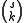
is the binomial coefficient
and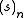
is the rising factorial. Newtonian series often appear in relations of the form seen in umbral calculus
.
gives
A proof for this identity can be obtained by showing that it satisfies the differential equation
The digamma function:
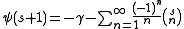
The Stirling numbers of the second kind are given by the finite sum
This formula is a special case of the kth forward difference of the monomial
xn evaluated at x = 0:
A related identity forms the basis of the Nörlund–Rice integral:
where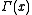
is the Gamma function
and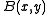
is the Beta function.
The trigonometric function
s have umbral
identities:
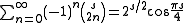
and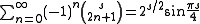
The umbral nature of these identities is a bit more clear by writing them in terms of the falling factorial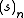
. The first few terms of the sin series are
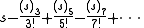
which can be recognized as resembling the Taylor series
for sin x, with (s)n standing in the place of xn.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Newtonian series, named after Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
, is a sum over a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
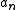written in the form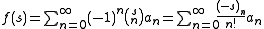where
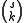
is the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
and
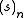is the rising factorial. Newtonian series often appear in relations of the form seen in umbral calculusUmbral calculus
In mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
.
List
The generalized binomial theoremBinomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
gives
A proof for this identity can be obtained by showing that it satisfies the differential equation
The digamma function:
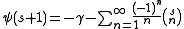
The Stirling numbers of the second kind are given by the finite sum
This formula is a special case of the kth forward difference of the monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
xn evaluated at x = 0:
A related identity forms the basis of the Nörlund–Rice integral:
where
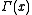is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
and
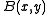is the Beta function.The trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s have umbral
Umbral calculus
In mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
identities:
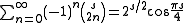
and
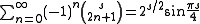
The umbral nature of these identities is a bit more clear by writing them in terms of the falling factorial
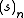. The first few terms of the sin series are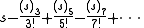which can be recognized as resembling the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for sin x, with (s)n standing in the place of xn.