Ensemble Kalman filter
Encyclopedia
The ensemble Kalman filter (EnKF) is a recursive filter
suitable for problems with a large number of variables, such as discretization
s of partial differential equation
s in geophysical models. The EnKF originated as a version of the Kalman filter
for large problems (essentially, the covariance matrix
is replaced by the sample covariance), and it is now an important data assimilation
component of ensemble forecasting
. EnKF is related to the particle filter
(in this context, a particle is the same thing as ensemble member) but the EnKF makes the assumption that all probability distributions involved are Gaussian; when it is applicable, it is much more efficient than the particle filter
.
implementation of the Bayesian update
problem: Given a probability density function
(pdf) of the state of the modeled system (the prior
, called often the forecast in geosciences) and the data likelihood, the Bayes theorem is used to obtain the pdf after the data likelihood has been taken into account (the posterior
, often called the analysis). This is called a Bayesian update. The Bayesian update is combined with advancing the model in time, incorporating new data from time to time. The original Kalman Filter
assumes that all pdfs are Gaussian (the Gaussian assumption) and provides algebraic formulas for the change of the mean
and the covariance matrix
by the Bayesian update, as well as a formula for advancing the covariance matrix in time provided the system is linear. However, maintaining the covariance matrix is not feasible computationally for high-dimensional systems. For this reason, EnKFs were developed. EnKFs represent the distribution of the system state using a collection of state vectors, called an ensemble, and replace the covariance matrix by the sample covariance computed from the ensemble. The ensemble is operated with as if it were a random sample
, but the ensemble members are really not independent
- the EnKF ties them together. One advantage of EnKFs is that advancing the pdf in time is achieved by simply advancing each member of the ensemble. For a survey of EnKF and related data assimilation techniques, see.
. Let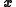
denote the 
-dimensional state vector
of a model, and assume that it has Gaussian probability distribution with mean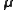
and covariance 
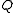, i.e., its pdf is
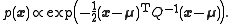
Here and below,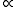
means proportional; a pdf is always scaled so that its integral over the whole space is one. This 
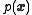, called the prior
, was evolved in time by running the model and now is to be updated to account for new data. It is natural to assume that the error distribution of the data is known; data have to come with an error estimate, otherwise they are meaningless. Here, the data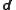
is assumed to have Gaussian pdf with covariance 
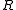and mean 
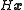, where 
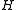is the so-called the observation matrix
. The covariance matrix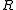
describes the estimate of the error of the data; if the random errors in the entries of the data vector 
are independent,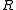 
is diagonal and its diagonal entries are the squares of the standard deviation
(“error size”) of the error of the corresponding entries of the data vector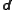
. The value 
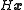is what the value of the data would be for the state 
in the absence of data errors. Then the probability density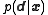 
of the data 
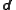conditional of the system state 
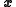, called the data likelihood
, is
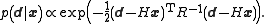
The pdf of the state and the data likelihood
are combined to give the new probability density of the system state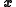
conditional on the value of the data 
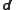(the posterior
) by the Bayes theorem,
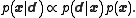
The data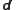
is fixed once it is received, so denote the posterior state by 
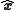instead of 
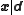and the posterior pdf by 
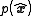. It can be shown by algebraic manipulations that the posterior pdf is also Gaussian,
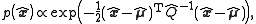
with the posterior mean
and covariance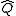 
given by the Kalman update formulas
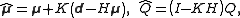
where
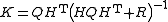
is the so-called Kalman gain matrix.
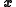. Instead, the pdf is represented by an ensemble
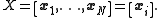
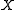is an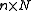 
matrix whose columns are the ensemble members, and it is called the prior ensemble. Ideally, ensemble members would form a sample
from the prior distribution. However, the ensemble members are not in general independent
except in the initial ensemble, since every EnKF step ties them together. They are deemed to be approximately independent, and all calculations proceed as if they actually were independent.
Replicate the data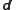
into an 
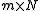matrix
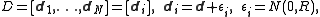
so that each column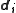
consists of the data vector 
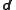plus a random vector from the 
-dimensional normal distribution 
. If, in addition, the columns of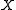 
are a sample from the prior probability
distribution, then the columns of
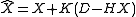
form a sample from the posterior probability
distribution. [To see this in the scalar case with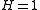
: Let 
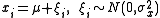, and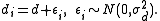 
Then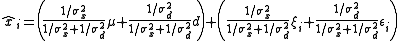 
. The first sum is the posterior mean, and the second sum, in view of the independence, has a variance 
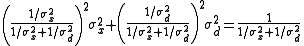, which is the posterior variance. ]
The EnKF is now obtained simply by replacing the state covariance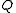
in Kalman gain matrix 
by the sample covariance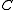 
computed from the ensemble members (called the ensemble covariance). That is: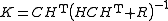 
and the data matrix 
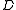are as above. The ensemble mean and the covariance are
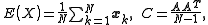
where
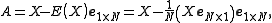
and
denotes the matrix of all ones of the indicated size.
The posterior ensemble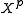
is then given by
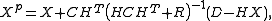
where the perturbed data matrix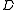
is as above.
Note that since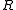
is a covariance matrix, it is always positive semidefinite and usually positive definite, so the inverse above exists and the formula can be implemented by the Cholesky decomposition
. In,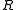
is replaced by the sample covariance 
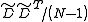where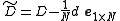 
and the inverse is replaced by a pseudoinverse
, computed using the Singular Value Decomposition
(SVD) .
Since these formulas are matrix operations with dominant Level 3 operations, they are suitable for efficient implementation using software packages such as LAPACK
(on serial and shared memory
computers) and ScaLAPACK
(on distributed memory
computers). Instead of computing the inverse of a matrix and multiplying by it, it is much better (several times cheaper and also more accurate) to compute the Cholesky decomposition
of the matrix and treat the multiplication by the inverse as solution of a linear system with many simultaneous right-hand sides.
. More specifically, define a function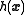 
of the form
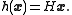
The function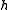
is called the observation function or, in the inverse problem
s context, the forward operator. The value of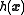
is what the value of the data would be for the state 
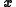assuming the measurement is exact. Then the posterior ensemble can be rewritten as
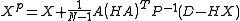
where
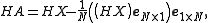
and
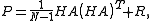
with
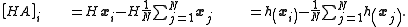
Consequently, the ensemble update can be computed by evaluating the observation function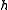
on each ensemble member once and the matrix 
does not need to be known explicitly. This formula holds also for an observation function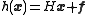 
with a fixed offset 
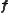, which also does not need to be known explicitly. The above formula has been commonly used for a nonlinear observation function 
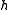, such as the position of a hurricane vortex
. In that case, the observation function is essentially approximated by a linear function from its values at ensemble members.
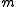of data points, the multiplication by 
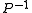becomes a bottleneck. The following alternative formula is advantageous when the number of data points 
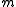is large (such as when assimilating gridded or pixel data) and the data error covariance matrix
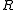is diagonal (which is the case when the data errors are uncorrelated), or cheap to decompose (such as banded due to limited covariance distance). Using the Sherman–Morrison–Woodbury formula
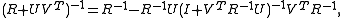
with
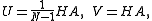
gives
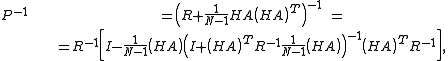
which requires only the solution of systems with the matrix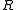
(assumed to be cheap) and of a system of size 
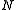with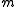 
right-hand sides. See for operation counts.
Since the ensemble covariance is rank deficient (there are many more state variables, typically millions, than the ensemble members, typically less than a hundred), it has large terms for pairs of points that are spatially distant. Since in reality the values of physical fields at distant locations are not that much correlated, the covariance matrix is tapered off artificially based on the distance, which gives rise to localized EnKF algorithms. These methods modify the covariance matrix used in the computations and, consequently, the posterior ensemble is no longer made only of linear combinations of the prior ensemble.
For nonlinear problems, EnKF can create posterior ensemble with non-physical states. This can be alleviated by regularization
, such as penalization
of states with large spatial gradient
s.
For problems with coherent features, such as firelines, squall line
s, and rain fronts, there is a need to adjust the simulation state by distorting the state in space as well as by an additive correction to the state. The morphing EnKF employs intermediate states, obtained by techniques borrowed from image registration
and morphing
, instead of linear combinations of states.
EnKFs rely on the Gaussian assumption, though they are of course used in practice for nonlinear problems, where the Gaussian assumption may not be satisfied. Related filters attempting to relax the Gaussian assumption in EnKF while preserving its advantages include filters that fit the state pdf with multiple Gaussian kernels, filters that approximate the state pdf by Gaussian mixtures, a variant of the particle filter
with computation of particle weights by density estimation
, and a variant of the particle filter with thick tailed
data pdf to alleviate particle filter degeneracy.
Recursive filter
In signal processing, a recursive filter is a type of filter which re-uses one or more of its outputs as an input. This feedback typically results in an unending impulse response , characterised by either exponentially growing, decaying, or sinusoidal signal output components.However, a recursive...
suitable for problems with a large number of variables, such as discretization
Discretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
s of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s in geophysical models. The EnKF originated as a version of the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
for large problems (essentially, the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
is replaced by the sample covariance), and it is now an important data assimilation
Data assimilation
Applications of data assimilation arise in many fields of geosciences, perhaps most importantly in weather forecasting and hydrology. Data assimilation proceeds by analysis cycles...
component of ensemble forecasting
Ensemble forecasting
Ensemble forecasting is a numerical prediction method that is used to attempt to generate a representative sample of the possible future states of a dynamical system...
. EnKF is related to the particle filter
Particle filter
In statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...
(in this context, a particle is the same thing as ensemble member) but the EnKF makes the assumption that all probability distributions involved are Gaussian; when it is applicable, it is much more efficient than the particle filter
Particle filter
In statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...
.
Introduction
The Ensemble Kalman Filter (EnKF) is a Monte CarloMonte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
implementation of the Bayesian update
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
problem: Given a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(pdf) of the state of the modeled system (the prior
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
, called often the forecast in geosciences) and the data likelihood, the Bayes theorem is used to obtain the pdf after the data likelihood has been taken into account (the posterior
Posterior probability
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
, often called the analysis). This is called a Bayesian update. The Bayesian update is combined with advancing the model in time, incorporating new data from time to time. The original Kalman Filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
assumes that all pdfs are Gaussian (the Gaussian assumption) and provides algebraic formulas for the change of the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
by the Bayesian update, as well as a formula for advancing the covariance matrix in time provided the system is linear. However, maintaining the covariance matrix is not feasible computationally for high-dimensional systems. For this reason, EnKFs were developed. EnKFs represent the distribution of the system state using a collection of state vectors, called an ensemble, and replace the covariance matrix by the sample covariance computed from the ensemble. The ensemble is operated with as if it were a random sample
Random sample
In statistics, a sample is a subject chosen from a population for investigation; a random sample is one chosen by a method involving an unpredictable component...
, but the ensemble members are really not independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
- the EnKF ties them together. One advantage of EnKFs is that advancing the pdf in time is achieved by simply advancing each member of the ensemble. For a survey of EnKF and related data assimilation techniques, see.
The Kalman Filter
Let us review first the Kalman filterKalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
. Let
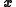denote the -dimensional state vectorState vector
*A state vector in general control systems describes the observed states of an object in state space, e.g. in variables of the degrees of freedom for motion *A state vector in general control systems describes the observed states of an object in state space, e.g. in variables of the degrees of...
of a model, and assume that it has Gaussian probability distribution with mean
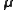and covariance 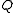, i.e., its pdf is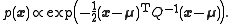Here and below,
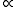means proportional; a pdf is always scaled so that its integral over the whole space is one. This 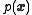, called the priorPrior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
, was evolved in time by running the model and now is to be updated to account for new data. It is natural to assume that the error distribution of the data is known; data have to come with an error estimate, otherwise they are meaningless. Here, the data
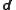is assumed to have Gaussian pdf with covariance 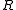and mean 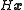, where 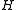is the so-called the observation matrixHat matrix
In statistics, the hat matrix, H, maps the vector of observed values to the vector of fitted values. It describes the influence each observed value has on each fitted value...
. The covariance matrix
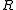describes the estimate of the error of the data; if the random errors in the entries of the data vector are independent, 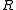is diagonal and its diagonal entries are the squares of the standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
(“error size”) of the error of the corresponding entries of the data vector
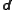. The value 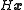is what the value of the data would be for the state in the absence of data errors. Then the probability density 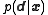of the data 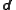conditional of the system state 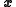, called the data likelihoodLikelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
, is
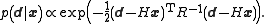
The pdf of the state and the data likelihood
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
are combined to give the new probability density of the system state
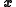conditional on the value of the data 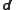(the posteriorPosterior probability
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
) by the Bayes theorem,
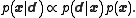
The data
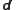is fixed once it is received, so denote the posterior state by 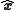instead of 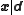and the posterior pdf by 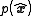. It can be shown by algebraic manipulations that the posterior pdf is also Gaussian,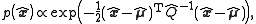with the posterior mean
and covariance 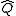given by the Kalman update formulas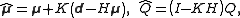where
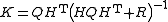
is the so-called Kalman gain matrix.
The Ensemble Kalman Filter
The EnKF is a Monte Carlo approximation of the Kalman filter, which avoids evolving the covariance matrix of the pdf of the state vector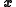. Instead, the pdf is represented by an ensemble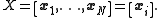 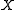is an 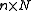matrix whose columns are the ensemble members, and it is called the prior ensemble. Ideally, ensemble members would form a sampleRandom sample
In statistics, a sample is a subject chosen from a population for investigation; a random sample is one chosen by a method involving an unpredictable component...
from the prior distribution. However, the ensemble members are not in general independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
except in the initial ensemble, since every EnKF step ties them together. They are deemed to be approximately independent, and all calculations proceed as if they actually were independent.
Replicate the data
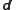into an 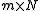matrix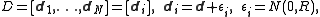so that each column
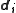consists of the data vector 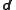plus a random vector from the -dimensional normal distribution . If, in addition, the columns of 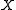are a sample from the prior probabilityPrior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
distribution, then the columns of
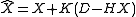
form a sample from the posterior probability
Posterior probability
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
distribution. [To see this in the scalar case with
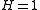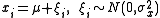: Let , and 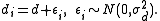Then 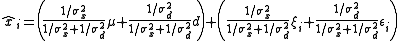. The first sum is the posterior mean, and the second sum, in view of the independence, has a variance 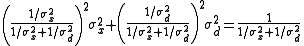, which is the posterior variance. ]The EnKF is now obtained simply by replacing the state covariance
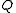in Kalman gain matrix by the sample covariance 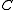computed from the ensemble members (called the ensemble covariance). That is: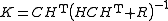 Basic formulation
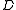Here we follow. Suppose the ensemble matrix and the data matrix are as above. The ensemble mean and the covariance are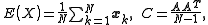where
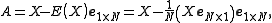
and
denotes the matrix of all ones of the indicated size.The posterior ensemble
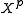is then given by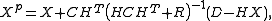where the perturbed data matrix
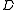is as above.Note that since
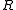is a covariance matrix, it is always positive semidefinite and usually positive definite, so the inverse above exists and the formula can be implemented by the Cholesky decompositionCholesky decomposition
In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
. In,
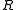is replaced by the sample covarianc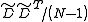e where 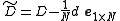and the inverse is replaced by a pseudoinversePseudoinverse
In mathematics, and in particular linear algebra, a pseudoinverse of a matrix is a generalization of the inverse matrix. The most widely known type of matrix pseudoinverse is the Moore–Penrose pseudoinverse, which was independently described by E. H. Moore in 1920, Arne Bjerhammar in 1951 and...
, computed using the Singular Value Decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
(SVD) .
Since these formulas are matrix operations with dominant Level 3 operations, they are suitable for efficient implementation using software packages such as LAPACK
LAPACK
-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
(on serial and shared memory
Shared memory
In computing, shared memory is memory that may be simultaneously accessed by multiple programs with an intent to provide communication among them or avoid redundant copies. Depending on context, programs may run on a single processor or on multiple separate processors...
computers) and ScaLAPACK
ScaLAPACK
The ScaLAPACK library includes a subset of LAPACK routines redesigned for distributed memory MIMD parallel computers. It is currently written in a Single-Program-Multiple-Data style using explicit message passing for interprocessor communication...
(on distributed memory
Distributed memory
In computer science, distributed memory refers to a multiple-processor computer system in which each processor has its own private memory. Computational tasks can only operate on local data, and if remote data is required, the computational task must communicate with one or more remote processors...
computers). Instead of computing the inverse of a matrix and multiplying by it, it is much better (several times cheaper and also more accurate) to compute the Cholesky decomposition
Cholesky decomposition
In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
of the matrix and treat the multiplication by the inverse as solution of a linear system with many simultaneous right-hand sides.
Observation matrix-free implementation
Since we have replaced the covariance matrix with ensemble covariance, this leads to a simpler formula where ensemble observations are directly used without explicitly specifying the matrix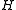. More specifically, define a function 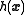of the form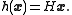The function
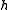is called the observation function or, in the inverse problemInverse problem
An inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system that we are interested in...
s context, the forward operator. The value of
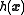is what the value of the data would be for the state 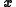assuming the measurement is exact. Then the posterior ensemble can be rewritten as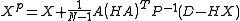where
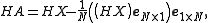
and
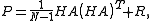
with
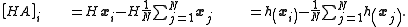
Consequently, the ensemble update can be computed by evaluating the observation function
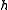on each ensemble member once and the matrix does not need to be known explicitly. This formula holds also for an observation function 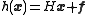with a fixed offset 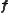, which also does not need to be known explicitly. The above formula has been commonly used for a nonlinear observation function 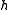, such as the position of a hurricane vortexVortex
A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
. In that case, the observation function is essentially approximated by a linear function from its values at ensemble members.
Implementation for a large number of data points
For a large number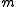 of data points, the multiplication by 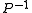becomes a bottleneck. The following alternative formula is advantageous when the number of data points 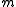is large (such as when assimilating gridded or pixel data) and the data error covariance matrixCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
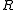is diagonal (which is the case when the data errors are uncorrelated), or cheap to decompose (such as banded due to limited covariance distance). Using the Sherman–Morrison–Woodbury formula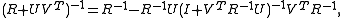with
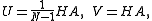
gives
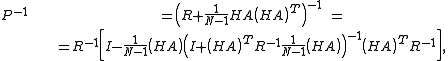
which requires only the solution of systems with the matrix
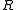(assumed to be cheap) and of a system of size 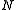with 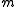right-hand sides. See for operation counts.Further extensions
The EnKF version described here involves randomization of data. For filters without randomization of data, see.Since the ensemble covariance is rank deficient (there are many more state variables, typically millions, than the ensemble members, typically less than a hundred), it has large terms for pairs of points that are spatially distant. Since in reality the values of physical fields at distant locations are not that much correlated, the covariance matrix is tapered off artificially based on the distance, which gives rise to localized EnKF algorithms. These methods modify the covariance matrix used in the computations and, consequently, the posterior ensemble is no longer made only of linear combinations of the prior ensemble.
For nonlinear problems, EnKF can create posterior ensemble with non-physical states. This can be alleviated by regularization
Tikhonov regularization
Tikhonov regularization, named for Andrey Tikhonov, is the most commonly used method of regularization of ill-posed problems. In statistics, the method is known as ridge regression, and, with multiple independent discoveries, it is also variously known as the Tikhonov-Miller method, the...
, such as penalization
Penalty method
Penalty methods are a certain class of algorithms for solving constrained optimization problems.A penalty method replaces a constrained optimization problem by a series of unconstrained problems whose solutions ideally converge to the solution of the original constrained problem...
of states with large spatial gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
s.
For problems with coherent features, such as firelines, squall line
Squall line
A squall line is a line of severe thunderstorms that can form along or ahead of a cold front. In the early 20th century, the term was used as a synonym for cold front. It contains heavy precipitation, hail, frequent lightning, strong straight-line winds, and possibly tornadoes and waterspouts....
s, and rain fronts, there is a need to adjust the simulation state by distorting the state in space as well as by an additive correction to the state. The morphing EnKF employs intermediate states, obtained by techniques borrowed from image registration
Image registration
Image registration is the process of transforming different sets of data into one coordinate system. Data may be multiple photographs, data from different sensors, from different times, or from different viewpoints. It is used in computer vision, medical imaging, military automatic target...
and morphing
Morphing
Morphing is a special effect in motion pictures and animations that changes one image into another through a seamless transition. Most often it is used to depict one person turning into another through technological means or as part of a fantasy or surreal sequence. Traditionally such a depiction...
, instead of linear combinations of states.
EnKFs rely on the Gaussian assumption, though they are of course used in practice for nonlinear problems, where the Gaussian assumption may not be satisfied. Related filters attempting to relax the Gaussian assumption in EnKF while preserving its advantages include filters that fit the state pdf with multiple Gaussian kernels, filters that approximate the state pdf by Gaussian mixtures, a variant of the particle filter
Particle filter
In statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...
with computation of particle weights by density estimation
Density estimation
In probability and statistics,density estimation is the construction of an estimate, based on observed data, of an unobservable underlying probability density function...
, and a variant of the particle filter with thick tailed
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
data pdf to alleviate particle filter degeneracy.
See also
- Data assimilationData assimilationApplications of data assimilation arise in many fields of geosciences, perhaps most importantly in weather forecasting and hydrology. Data assimilation proceeds by analysis cycles...
- Kalman filterKalman filterIn statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
- Numerical weather prediction#Ensembles
- Particle filterParticle filterIn statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...
- Recursive Bayesian estimationRecursive Bayesian estimationRecursive Bayesian estimation, also known as a Bayes filter, is a general probabilistic approach for estimating an unknown probability density function recursively over time using incoming measurements and a mathematical process model.-In robotics:...
External links
- (EAKF-CMAQ: DEVELOPMENT AND INITIAL EVALUATION OF AN ENSEMBLE ADJUSTMENT KALMAN FILTER BASED DATA ASSIMILATION FOR CO)