Recursive Bayesian estimation
Encyclopedia
Recursive Bayesian estimation, also known as a Bayes filter, is a general probabilistic approach for estimating
an unknown probability density function
recursively over time using incoming measurements and a mathematical process model.
for calculating the probabilities of multiple beliefs to allow a robot
to infer its position and orientation. Essentially, Bayes filters allow robots to continuously update their most likely position within a coordinate system, based on the most recently acquired sensor data. This is a recursive algorithm. It consists of two parts: prediction and innovation. If the variables are linear and gauss-distributed the Bayes filter becomes equal to the Kalman filter
.
In a simple example, a robot moving throughout a grid may have several different sensors that provide it with information about its surroundings. The robot may start out with certainty that it is at position (0,0). However, as it moves farther and farther from its original position, the robot has continuously less certainty about its position; using a Bayes filter, a probability can be assigned to the robot's belief about its current position, and that probability can be continuously updated from additional sensor information.
is assumed to be an unobserved Markov process
, and the measurements
are the observed states of a Hidden Markov Model
(HMM). The following picture presents a Bayesian Network of a HMM.
Because of the Markov assumption, the probability of the current true state given the immediately previous one is conditionally independent of the other earlier states.
Similarly, the measurement at the k-th timestep is dependent only upon the current state, so is conditionally independent of all other states given the current state.
Using these assumptions the probability distribution over all states of the HMM can be written simply as:
However, when using the Kalman filter to estimate the state x, the probability distribution of interest is associated with the current states conditioned on the measurements up to the current timestep. (This is achieved by marginalising out the previous states and dividing by the probability of the measurement set.)
This leads to the predict and update steps of the Kalman filter written probabilistically. The probability distribution associated with the predicted state is the sum (integral) of the products of the probability distribution associated with the transition from the (k - 1)-th timestep to the k-th and the probability distribution associated with the previous state, over all possible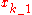
.
The probability distribution of update is proportional to the product of the measurement likelihood and the predicted state.
The denominator
is constant relative to
, so we can always substitute it for a coefficient 
, which can usually be ignored in practice. The numerator can be calculated and then simply normalized, since its integral must be unitary.
The method is named:
filtering: when we estimate the current value given past observations,
smoothing
: when estimating past values given present and past measures, and
prediction: when estimating a probable future value.
The notion of Sequential Bayesian filtering is extensively used in control
and robotics
.
Density estimation
In probability and statistics,density estimation is the construction of an estimate, based on observed data, of an unobservable underlying probability density function...
an unknown probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
recursively over time using incoming measurements and a mathematical process model.
In robotics
A Bayes filter is an algorithm used in computer scienceComputer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
for calculating the probabilities of multiple beliefs to allow a robot
Robot
A robot is a mechanical or virtual intelligent agent that can perform tasks automatically or with guidance, typically by remote control. In practice a robot is usually an electro-mechanical machine that is guided by computer and electronic programming. Robots can be autonomous, semi-autonomous or...
to infer its position and orientation. Essentially, Bayes filters allow robots to continuously update their most likely position within a coordinate system, based on the most recently acquired sensor data. This is a recursive algorithm. It consists of two parts: prediction and innovation. If the variables are linear and gauss-distributed the Bayes filter becomes equal to the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
.
In a simple example, a robot moving throughout a grid may have several different sensors that provide it with information about its surroundings. The robot may start out with certainty that it is at position (0,0). However, as it moves farther and farther from its original position, the robot has continuously less certainty about its position; using a Bayes filter, a probability can be assigned to the robot's belief about its current position, and that probability can be continuously updated from additional sensor information.
Model
The true state is assumed to be an unobserved Markov processMarkov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
, and the measurements
are the observed states of a Hidden Markov ModelHidden Markov model
A hidden Markov model is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved states. An HMM can be considered as the simplest dynamic Bayesian network. The mathematics behind the HMM was developed by L. E...
(HMM). The following picture presents a Bayesian Network of a HMM.
Similarly, the measurement at the k-th timestep is dependent only upon the current state, so is conditionally independent of all other states given the current state.
Using these assumptions the probability distribution over all states of the HMM can be written simply as:
However, when using the Kalman filter to estimate the state x, the probability distribution of interest is associated with the current states conditioned on the measurements up to the current timestep. (This is achieved by marginalising out the previous states and dividing by the probability of the measurement set.)
This leads to the predict and update steps of the Kalman filter written probabilistically. The probability distribution associated with the predicted state is the sum (integral) of the products of the probability distribution associated with the transition from the (k - 1)-th timestep to the k-th and the probability distribution associated with the previous state, over all possible
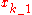.The probability distribution of update is proportional to the product of the measurement likelihood and the predicted state.
The denominator
is constant relative to
, so we can always substitute it for a coefficient , which can usually be ignored in practice. The numerator can be calculated and then simply normalized, since its integral must be unitary.Applications
- Kalman filterKalman filterIn statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
, a recursive Bayesian filter for multivariate normal distributions - Particle filterParticle filterIn statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...
, a sequential Monte Carlo (SMC) based technique, which models the PDFProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
using a set of discrete points - Grid-based estimators, which subdivide the PDF into a discrete grid
Sequential Bayesian filtering
Sequential Bayesian filtering is the extension of the Bayesian estimation for the case when the observed value changes in time. It is a method to estimate the real value of an observed variable that evolves in time.The method is named:
filtering: when we estimate the current value given past observations,
smoothing
Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. Many different algorithms are used in smoothing...
: when estimating past values given present and past measures, and
prediction: when estimating a probable future value.
The notion of Sequential Bayesian filtering is extensively used in control
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
and robotics
Robotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
.
External links
- A Tutorial on Particle Filters for On-line Non-linear/Non-Gaussian Bayesian Tracking, IEEE Transactions on Signal Processing (2001)
- A survey of probabilistic models, using the Bayesian Programming methodology as a unifying framework