Statistical signal processing
Encyclopedia
Statistical signal processing is an area of Applied Mathematics
and Signal Processing
that treats signals as stochastic process
es, dealing with their statistical properties (e.g., mean
, covariance
, etc.). Because of its very broad range of application Statistical signal processing is taught at the graduate level in either Electrical Engineering
, Applied Mathematics
, Pure Mathematics
/Statistics
, or even Biomedical Engineering
and Physics
departments around the world, although important applications exist in almost all scientific fields.
In many areas signals are modeled as functions consisting of both deterministic and stochastic
components. A simple example and also a common model of many statistical systems is a signal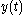
that consists of a deterministic part 
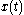added to noise which can be modeled in many situations as white Gaussian noise
:
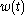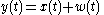
where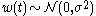
White noise
simply means that the noise process is completely uncorrelated. As a result, its autocorrelation
function is an impulse
:
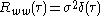
where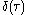
is the Dirac delta function
.
Given information about a statistical system and the random variable
from which it is derived, we can increase our knowledge of the output signal; conversely, given the statistical properties of the output signal, we can infer the properties of the underlying random variable. These statistical techniques are developed in the fields of estimation theory
, detection theory
, and numerous related fields that rely on statistical information to maximize their efficiency.
For example, the Computation of Average Transients (CAT) is used routinely in FT-NMR spectroscopy
(nuclear magnetic resonance
) to improve the signal-noise ratio of nmr spectra. The signal is measured repeatedly n times and then averaged.
Assuming that the noise is white and that its variance is constant in time it follows by error propagation that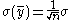
Thus, if 10,000 measurements are averaged the signal to noise ratio is increased by a factor of 100, enabling the measurement of 13C
NMR spectra at natural abundance (1.1%) of 13C.
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
and Signal Processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
that treats signals as stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es, dealing with their statistical properties (e.g., mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
, covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
, etc.). Because of its very broad range of application Statistical signal processing is taught at the graduate level in either Electrical Engineering
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, Applied Mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, Pure Mathematics
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
/Statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, or even Biomedical Engineering
Biomedical engineering
Biomedical Engineering is the application of engineering principles and design concepts to medicine and biology. This field seeks to close the gap between engineering and medicine: It combines the design and problem solving skills of engineering with medical and biological sciences to improve...
and Physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
departments around the world, although important applications exist in almost all scientific fields.
In many areas signals are modeled as functions consisting of both deterministic and stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
components. A simple example and also a common model of many statistical systems is a signal
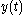that consists of a deterministic part 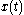added to noise which can be modeled in many situations as white Gaussian noiseGaussian noise
Gaussian noise is statistical noise that has its probability density function equal to that of the normal distribution, which is also known as the Gaussian distribution. In other words, the values that the noise can take on are Gaussian-distributed. A special case is white Gaussian noise, in which...
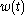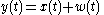
:where
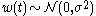
White noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
simply means that the noise process is completely uncorrelated. As a result, its autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
function is an impulse
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
:
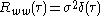
where
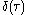is the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
.
Given information about a statistical system and the random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
from which it is derived, we can increase our knowledge of the output signal; conversely, given the statistical properties of the output signal, we can infer the properties of the underlying random variable. These statistical techniques are developed in the fields of estimation theory
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
, detection theory
Detection theory
Detection theory, or signal detection theory, is a means to quantify the ability to discern between information-bearing energy patterns and random energy patterns that distract from the information Detection theory, or signal detection theory, is a means to quantify the ability to discern between...
, and numerous related fields that rely on statistical information to maximize their efficiency.
For example, the Computation of Average Transients (CAT) is used routinely in FT-NMR spectroscopy
NMR spectroscopy
Nuclear magnetic resonance spectroscopy, most commonly known as NMR spectroscopy, is a research technique that exploits the magnetic properties of certain atomic nuclei to determine physical and chemical properties of atoms or the molecules in which they are contained...
(nuclear magnetic resonance
Nuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
) to improve the signal-noise ratio of nmr spectra. The signal is measured repeatedly n times and then averaged.
Assuming that the noise is white and that its variance is constant in time it follows by error propagation that
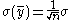
Thus, if 10,000 measurements are averaged the signal to noise ratio is increased by a factor of 100, enabling the measurement of 13C
Carbon
Carbon is the chemical element with symbol C and atomic number 6. As a member of group 14 on the periodic table, it is nonmetallic and tetravalent—making four electrons available to form covalent chemical bonds...
NMR spectra at natural abundance (1.1%) of 13C.
Further reading
- Kainam Thomas Wonghttp://www.eie.polyu.edu.hk/~enktwong/: Statistical Signal Processing lecture noteshttp://ece.uwaterloo.ca/~ece603/ at the University of Waterloo, Canada.
- Ali H. SayedAli H. SayedAli H. Sayed is Professor of Electrical Engineering at the University of California, Los Angeles , where he teaches and conducts research on Adaptation, Learning, Statistical Signal Processing, and Signal Processing for Communications. He is the Director of the UCLA Adaptive Systems Laboratory...
, Adaptive Filters, Wiley, NJ, 2008, ISBN 978-0-470-25388-5. - Thomas KailathThomas KailathThomas Kailath is an Indian electrical engineer, information theorist, control engineer, entrepreneur and the Hitachi America Professor of Engineering, Emeritus, at Stanford University...
, Ali H. SayedAli H. SayedAli H. Sayed is Professor of Electrical Engineering at the University of California, Los Angeles , where he teaches and conducts research on Adaptation, Learning, Statistical Signal Processing, and Signal Processing for Communications. He is the Director of the UCLA Adaptive Systems Laboratory...
, and Babak HassibiBabak HassibiBabak Hassibi is an Iranian-American electrical engineer who is currently professor of Electrical Engineering and head of the Department of Electrical Engineering at the California Institute of Technology ....
, Linear Estimation, Prentice-Hall, NJ, 2000, ISBN 978-0-13-022464-4.