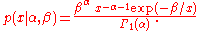Inverse-Wishart distribution
Encyclopedia
In statistics
, the inverse Wishart distribution, also called the inverted Wishart distribution, is a probability distribution
defined on real-valued positive-definite
matrices
. In Bayesian statistics
it is used as the conjugate prior
for the covariance matrix of a
multivariate normal distribution.
We say follows an inverse Wishart distribution, denoted as
follows an inverse Wishart distribution, denoted as 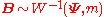 , if its inverse
, if its inverse 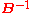 has a Wishart distribution
has a Wishart distribution 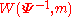 .
.
of the inverse Wishart is:
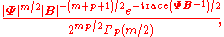
where and
and  are
are  positive definite matrices, and Γp(·) is the multivariate gamma function
positive definite matrices, and Γp(·) is the multivariate gamma function
.
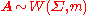 and
and  is of size
is of size 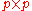 , then
, then 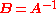 has an inverse Wishart distribution
has an inverse Wishart distribution  with probability density function:
with probability density function: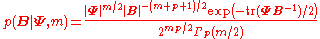
where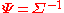 and
and 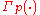 is the multivariate gamma function
is the multivariate gamma function
.
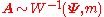 has an inverse Wishart distribution. Partition the matrices
has an inverse Wishart distribution. Partition the matrices  and
and  conformably with each other
conformably with each other
where and
and 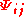 are
are 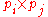 matrices, then we have
matrices, then we have
i)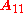 is independent of
is independent of 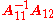 and
and  , where
, where 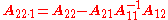 is the Schur complement
is the Schur complement
of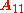 in
in  ;
;
ii)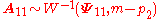 ;
;
iii)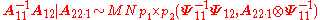 , where
, where  is a matrix normal distribution
is a matrix normal distribution
;
iv)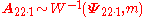
 whose prior
whose prior
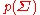 has a
has a 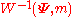 distribution. If the observations
distribution. If the observations 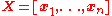 are independent p-variate Gaussian variables drawn from a
are independent p-variate Gaussian variables drawn from a 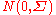 distribution, then the conditional distribution
distribution, then the conditional distribution  has a
has a  distribution, where
distribution, where  is
is  times the sample covariance matrix.
times the sample covariance matrix.
Because the prior and posterior distributions are the same family, we say the inverse Wishart distribution is conjugate
to the multivariate Gaussian.
Due to its conjugacy to the multivariate Gaussian, it is possible to "integrate out" the Gaussian's parameter .
.
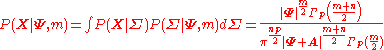
(this is useful because the variance matrix is not known in practice, but because
is not known in practice, but because  is known a priori, and
is known a priori, and  can be obtained from the data, the right hand side can be evaluated directly).
can be obtained from the data, the right hand side can be evaluated directly).
The mean: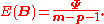
The variance of each element of :
: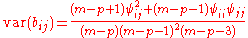
The variance of the diagonal uses the same formula as above with , which simplifies to:
, which simplifies to:
specialization of the inverse-Wishart distribution is the inverse-gamma distribution. With (i.e. univariate) and
(i.e. univariate) and 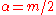 ,
, 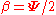 and
and  the probability density function
the probability density function
of the inverse-Wishart distribution becomes
i.e., the inverse-gamma distribution, where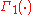 is the ordinary Gamma function
is the ordinary Gamma function
.
A generalization is the normal-inverse-Wishart distribution.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the inverse Wishart distribution, also called the inverted Wishart distribution, is a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
defined on real-valued positive-definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. In Bayesian statistics
Bayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
it is used as the conjugate prior
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
for the covariance matrix of a
multivariate normal distribution.
We say
 follows an inverse Wishart distribution, denoted as
follows an inverse Wishart distribution, denoted as 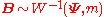 , if its inverse
, if its inverse 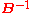 has a Wishart distribution
has a Wishart distribution 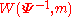 .
.Density
The probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the inverse Wishart is:
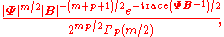
where
 and
and  are
are  positive definite matrices, and Γp(·) is the multivariate gamma function
positive definite matrices, and Γp(·) is the multivariate gamma functionMultivariate gamma function
In mathematics, the multivariate Gamma function, Γp, is a generalization of the Gamma function. It is useful in multivariate statistics, appearing in the probability density function of the Wishart and Inverse Wishart distributions....
.
Distribution of the inverse of a Wishart-distributed matrix
If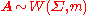 and
and  is of size
is of size 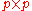 , then
, then 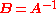 has an inverse Wishart distribution
has an inverse Wishart distribution  with probability density function:
with probability density function: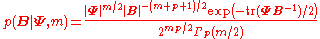
where
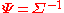 and
and 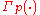 is the multivariate gamma function
is the multivariate gamma functionMultivariate gamma function
In mathematics, the multivariate Gamma function, Γp, is a generalization of the Gamma function. It is useful in multivariate statistics, appearing in the probability density function of the Wishart and Inverse Wishart distributions....
.
Marginal and conditional distributions from an inverse Wishart-distributed matrix
Suppose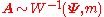 has an inverse Wishart distribution. Partition the matrices
has an inverse Wishart distribution. Partition the matrices  and
and  conformably with each other
conformably with each other
where
 and
and 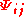 are
are 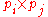 matrices, then we have
matrices, then we havei)
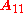 is independent of
is independent of 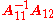 and
and  , where
, where 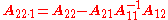 is the Schur complement
is the Schur complementSchur complement
In linear algebra and the theory of matrices,the Schur complement of a matrix block is defined as follows.Suppose A, B, C, D are respectivelyp×p, p×q, q×p...
of
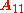 in
in  ;
;ii)
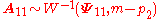 ;
;iii)
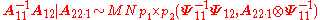 , where
, where  is a matrix normal distribution
is a matrix normal distributionMatrix normal distribution
The matrix normal distribution is a probability distribution that is a generalization of the normal distribution to matrix-valued random variables.- Definition :...
;
iv)
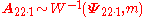
Conjugate distribution
Suppose we wish to make inference about a covariance matrix whose prior
whose priorA priori (statistics)
In statistics, a priori knowledge is prior knowledge about a population, rather than that estimated by recent observation. It is common in Bayesian inference to make inferences conditional upon this knowledge, and the integration of a priori knowledge is the central difference between the Bayesian...
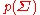 has a
has a 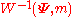 distribution. If the observations
distribution. If the observations 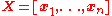 are independent p-variate Gaussian variables drawn from a
are independent p-variate Gaussian variables drawn from a 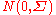 distribution, then the conditional distribution
distribution, then the conditional distribution  has a
has a  distribution, where
distribution, where  is
is  times the sample covariance matrix.
times the sample covariance matrix.Because the prior and posterior distributions are the same family, we say the inverse Wishart distribution is conjugate
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
to the multivariate Gaussian.
Due to its conjugacy to the multivariate Gaussian, it is possible to "integrate out" the Gaussian's parameter
 .
.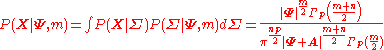
(this is useful because the variance matrix
 is not known in practice, but because
is not known in practice, but because  is known a priori, and
is known a priori, and  can be obtained from the data, the right hand side can be evaluated directly).
can be obtained from the data, the right hand side can be evaluated directly).Moments
The following is based on Press, S. J. (1982) "Applied Multivariate Analysis", 2nd ed. (Dover Publications, New York), after reparameterizing the degree of freedom to be consistent with the p.d.f. definition above.The mean:
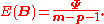
The variance of each element of
 :
: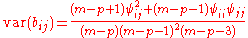
The variance of the diagonal uses the same formula as above with
 , which simplifies to:
, which simplifies to:
Related distributions
A univariateUnivariate
In mathematics, univariate refers to an expression, equation, function or polynomial of only one variable. Objects of any of these types but involving more than one variable may be called multivariate...
specialization of the inverse-Wishart distribution is the inverse-gamma distribution. With
 (i.e. univariate) and
(i.e. univariate) and 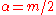 ,
, 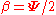 and
and  the probability density function
the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the inverse-Wishart distribution becomes
i.e., the inverse-gamma distribution, where
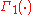 is the ordinary Gamma function
is the ordinary Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
A generalization is the normal-inverse-Wishart distribution.