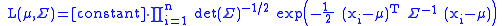Estimation of covariance matrices
Encyclopedia
In statistics
, sometimes the covariance matrix
of a multivariate random variable
is not known but has to be estimated
. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution. Simple cases, where observations are complete, can be dealt with by using the sample covariance matrix. The sample covariance matrix (SCM) is an unbiased and efficient estimator
of the covariance matrix if the space of covariance matrices is viewed as an extrinsic convex cone
in Rp×p; however, measured using the intrinsic geometry
of positive-definite matrices
, the SCM is a biased and inefficient estimator. In addition, if the random variable has normal distribution, the sample covariance matrix has Wishart distribution and a slightly differently scaled version of it is the maximum likelihood estimate. Cases involving missing data require deeper considerations. Another issue is the robustness
to outlier
s: "Sample covariance matrices are extremely sensitive to outliers".
Statistical analyses of multivariate data often involve exploratory studies of the way in which the variables change in relation to one another and this may be followed up by explicit statistical models involving the covariance matrix of the variables. Thus the estimation of covariance matrices directly from observational data plays two roles:
Estimates of covariance matrices are required at the initial stages of principal component analysis and factor analysis
, and are also involved in versions of regression analysis
that treat the dependent variables in a data-set, jointly with the independent variable
as the outcome of a random sample.
consisting of n independent observations x1,..., xn of a p-dimensional random variable
X ∈ Rp×1 (a p×1 column-vector), an unbiased
estimator
of the (p×p) covariance matrix
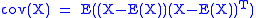
is the sample covariance matrix
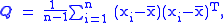
where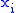
is the i-th observation of the p-dimensional random variable, and
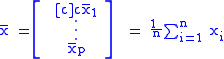
is the sample mean.
This is true regardless of the distribution of the random variable X, provided of course that the theoretical means and covariances exist. The reason for the factor n − 1 rather than n is essentially the same as the reason for the same factor appearing in unbiased estimates of sample variances and sample covariances
, which relates to the fact that the mean is not known and is replaced by the sample mean.
In cases where the distribution of the random variable
X is known to be within a certain family of distributions, other estimates may be derived on the basis of that assumption. A well-known instance is when the random variable
X is normally distributed: in this case the maximum likelihood
estimator
of the covariance matrix is slightly different from the unbiased estimate, and is given by
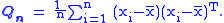
A derivation of this result is given below. Clearly, the difference between the unbiased estimator and the maximum likelihood estimator diminishes for large n.
In the general case, the unbiased estimate of the covariance matrix provides an acceptable estimate when the data vectors in the observed data set are all complete: that is they contain no missing elements
. One approach to estimating the covariance matrix is to treat the estimation of each variance or pairwise covariance separately, and to use all the observations for which both variables have valid values. Assuming the missing data are missing at random this results in an estimate for the covariance matrix which is unbiased. However, for many applications this estimate may not be acceptable because the estimated covariance matrix is not guaranteed to be positive semi-definite. This could lead to estimated correlations having absolute values which are greater than one, and/or a non-invertible covariance matrix.
and the probability density function
of X is
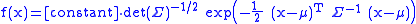
where μ ∈ Rp×1 is the expected value
, the covariance matrix
Σ is the higher-dimensional analog of what in one dimension would be the variance
, and
normalizes density so that it integrates to 1.
Suppose now that X1, ..., Xn are independent
and identically distributed with the distribution above. Based on the observed values x1, ..., xn of this sample, we wish to estimate Σ.
It is fairly readily shown that the maximum-likelihood
estimate of the mean vector μ is the "sample mean" vector:
See the section on estimation in the article on the normal distribution for details; the process here is similar.
Since the estimate of μ does not depend on Σ, we can just substitute it for μ in the likelihood function
, getting
and then seek the value of Σ that maximizes this (in practice it is easier to work with log L).
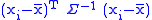as the trace of a 1×1 matrix.
This makes it possible to use the identity tr(AB) = tr(BA) whenever A and B are matrices so shaped that both products exist.
We get
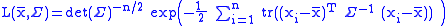
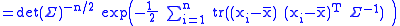
(so now we are taking the trace of a p×p matrix)
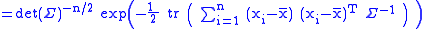
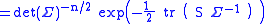
where
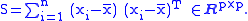
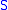is sometimes called the scatter matrix
, which is positive definite if
and at least n of the observations are linearly independent (which we will assume).
of linear algebra
that a positive-definite symmetric matrix S has a unique positive-definite symmetric square root S1/2. We can again use the "cyclic property" of the trace to write
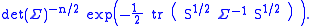
Let B = S1/2 Σ −1 S1/2. Then the expression above becomes
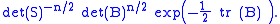
The positive-definite matrix B can be diagonalized, and then the problem of finding the value of B that maximizes
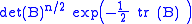
reduces to the problem of finding the values of the diagonal entries λ1, ..., λp that maximize
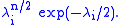
This is just a calculus problem and we get λi = n, so that B = n Ip, i.e., n times the p×p identity matrix.
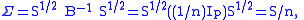
i.e., the p×p "sample covariance matrix"
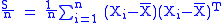
is the maximum-likelihood estimator of the "population covariance matrix" Σ. At this point we are using a capital X rather than a lower-case x because we are thinking of it "as an estimator rather than as an estimate", i.e., as something random whose probability distribution we could profit by knowing. The random matrix S can be shown to have a Wishart distribution with n − 1 degrees of freedom. That is:
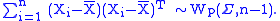
formulae (see also differential of a determinant and differential of the inverse matrix). It also verifies the aforementioned fact about the maximum likelihood estimate of the mean. Re-write the likelihood in the log form using the trace trick:
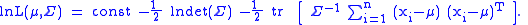
The differential of this log-likelihood is
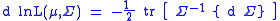
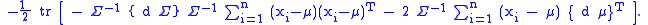
It naturally breaks down into the part related to the estimation of the mean, and to the part related to the estimation of the variance. The first order condition for maximum,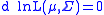
, is satisfied when the terms multiplying 
and 
are identically zero. Assuming (the maximum likelihood estimate of) 
is non-singular, the first order condition for the estimate of the mean vector is
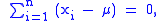
which leads to the maximum likelihood estimator
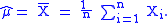
This lets us simplify
as defined above. Then the terms involving 
in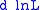 
can be combined as
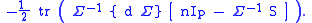
The first order condition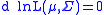
will hold when the term in the square bracket is (matrix-valued) zero. Pre-multiplying the latter by 
and dividing by 
gives
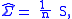
which of course coincides with the canonical derivation given earlier.
Dwyer points out that decomposition into two terms such as appears above is "unnecessary" and derives the estimator in two lines of working. Note that it may be not trivial to show that such derived estimator is the unique global maximizer for likelihood function.
of n independent observations x1,..., xn of a p-dimensional zero-mean Gaussian random variable X with covariance R, the maximum likelihood
estimator
of R is given by
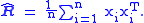
The parameter R belongs to the set of positive-definite matrices
, which is a Riemannian manifold
, not a vector space
, hence the usual vector-space notions of expectation
, i.e. "E[R^]", and estimator bias must be generalized to manifolds to make sense of the problem of covariance matrix estimation. This can be done by defining the expectation of an manifold-valued estimator R^ with respect to the manifold-valued point R as
where
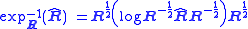
are the exponential map
and inverse exponential map, respectively, "exp" and "log" denote the ordinary matrix exponential
and matrix logarithm, and E[·] is the ordinary expectation operator defined on a vector space, in this case the tangent space
of the manifold.
of the SCM estimator R^ is defined to be
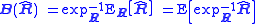
The intrinsic estimator bias is then given by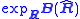
.
For complex
Gaussian random variables, this bias vector field can be shown to equal
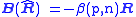
where
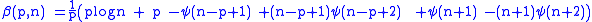
and ψ(·) is the digamma function. The intrinsic bias of the sample covariance matrix equals
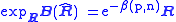
and the SCM is asymptotically unbiased as n → ∞.
Similarly, the intrinsic inefficiency
of the sample covariance matrix depends upon the Riemannian curvature of the space of positive-define matrices.
As an alternative, many methods have been suggested to improve the estimation of the covariance matrix. All of these approaches rely on the concept of shrinkage. This is implicit in Bayesian methods, in penalized maximum likelihood
methods, and explicit in the Stein-type shrinkage approach.
A simple version of a shrinkage estimator of the covariance matrix is constructed as follows. One considers a convex combination
of the empirical estimator with some suitable chosen target, e.g., the diagonal matrix. Subsequently, the mixing parameter
is selected to maximize the expected accuracy of the shrunken estimator. This can be done by cross-validation, or by using an analytic estimate of the shrinkage intensity. The resulting regularized estimator can be shown to outperform the maximum likelihood estimator for small samples. For large samples, the shrinkage intensity will reduce to zero, hence in
this case the shrinkage estimator will be identical to the empirical estimator. Apart from increased efficiency the shrinkage estimate has the additional advantage that it is always positive definite and well conditioned.
A review on this topic is given, e.g., in Schäfer and Strimmer 2005.
A covariance shrinkage estimator is implemented in the R package "corpcor".
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, sometimes the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of a multivariate random variable
Multivariate random variable
In mathematics, probability, and statistics, a multivariate random variable or random vector is a list of mathematical variables each of whose values is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value.More formally, a multivariate random...
is not known but has to be estimated
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution. Simple cases, where observations are complete, can be dealt with by using the sample covariance matrix. The sample covariance matrix (SCM) is an unbiased and efficient estimator
Efficiency (statistics)
In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
of the covariance matrix if the space of covariance matrices is viewed as an extrinsic convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
in Rp×p; however, measured using the intrinsic geometry
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
of positive-definite matrices
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, the SCM is a biased and inefficient estimator. In addition, if the random variable has normal distribution, the sample covariance matrix has Wishart distribution and a slightly differently scaled version of it is the maximum likelihood estimate. Cases involving missing data require deeper considerations. Another issue is the robustness
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
to outlier
Outlier
In statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....
s: "Sample covariance matrices are extremely sensitive to outliers".
Statistical analyses of multivariate data often involve exploratory studies of the way in which the variables change in relation to one another and this may be followed up by explicit statistical models involving the covariance matrix of the variables. Thus the estimation of covariance matrices directly from observational data plays two roles:
- to provide initial estimates that can be used to study the inter-relationships;
- to provide sample estimates that can be used for model checking.
Estimates of covariance matrices are required at the initial stages of principal component analysis and factor analysis
Factor analysis
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved, uncorrelated variables called factors. In other words, it is possible, for example, that variations in three or four observed variables...
, and are also involved in versions of regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
that treat the dependent variables in a data-set, jointly with the independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
as the outcome of a random sample.
Estimation in a general context
Given a sampleSample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
consisting of n independent observations x1,..., xn of a p-dimensional random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X ∈ Rp×1 (a p×1 column-vector), an unbiased
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of the (p×p) covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
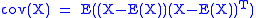
is the sample covariance matrix
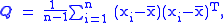
where
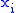is the i-th observation of the p-dimensional random variable, and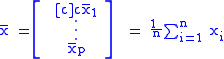is the sample mean.
This is true regardless of the distribution of the random variable X, provided of course that the theoretical means and covariances exist. The reason for the factor n − 1 rather than n is essentially the same as the reason for the same factor appearing in unbiased estimates of sample variances and sample covariances
Sample mean and sample covariance
The sample mean or empirical mean and the sample covariance are statistics computed from a collection of data on one or more random variables. The sample mean is a vector each of whose elements is the sample mean of one of the random variables that is, each of whose elements is the average of the...
, which relates to the fact that the mean is not known and is replaced by the sample mean.
In cases where the distribution of the random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X is known to be within a certain family of distributions, other estimates may be derived on the basis of that assumption. A well-known instance is when the random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X is normally distributed: in this case the maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of the covariance matrix is slightly different from the unbiased estimate, and is given by
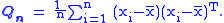
A derivation of this result is given below. Clearly, the difference between the unbiased estimator and the maximum likelihood estimator diminishes for large n.
In the general case, the unbiased estimate of the covariance matrix provides an acceptable estimate when the data vectors in the observed data set are all complete: that is they contain no missing elements
Missing values
In statistics, missing data, or missing values, occur when no data value is stored for the variable in the current observation. Missing data are a common occurrence and can have a significant effect on the conclusions that can be drawn from the data....
. One approach to estimating the covariance matrix is to treat the estimation of each variance or pairwise covariance separately, and to use all the observations for which both variables have valid values. Assuming the missing data are missing at random this results in an estimate for the covariance matrix which is unbiased. However, for many applications this estimate may not be acceptable because the estimated covariance matrix is not guaranteed to be positive semi-definite. This could lead to estimated correlations having absolute values which are greater than one, and/or a non-invertible covariance matrix.
Maximum-likelihood estimation for the multivariate normal distribution
A random vector X ∈ Rp×1 (a p×1 "column vector") has a multivariate normal distribution with a nonsingular covariance matrix Σ precisely if Σ ∈ Rp × p is a positive-definite matrixPositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
and the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of X is
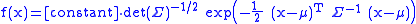
where μ ∈ Rp×1 is the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
Σ is the higher-dimensional analog of what in one dimension would be the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, and
normalizes density so that it integrates to 1.Suppose now that X1, ..., Xn are independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
and identically distributed with the distribution above. Based on the observed values x1, ..., xn of this sample, we wish to estimate Σ.
First steps
The likelihood function is:
It is fairly readily shown that the maximum-likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimate of the mean vector μ is the "sample mean" vector:
See the section on estimation in the article on the normal distribution for details; the process here is similar.
Since the estimate of μ does not depend on Σ, we can just substitute it for μ in the likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
, getting
and then seek the value of Σ that maximizes this (in practice it is easier to work with log L).
The trace of a 1 × 1 matrix
Now we come to the first surprising step: regard the scalarScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
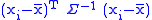as the trace of a 1×1 matrix.This makes it possible to use the identity tr(AB) = tr(BA) whenever A and B are matrices so shaped that both products exist.
We get
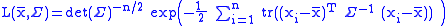
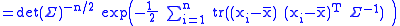
(so now we are taking the trace of a p×p matrix)
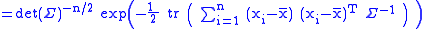
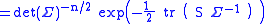
where
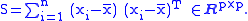
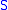is sometimes called the scatter matrixScatter matrix
In multivariate statistics and probability theory, the scatter matrix is a statistic that is used to make estimates of the covariance matrix of the multivariate normal distribution.-Definition:...
, which is positive definite if
and at least n of the observations are linearly independent (which we will assume).Using the spectral theorem
It follows from the spectral theoremSpectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
that a positive-definite symmetric matrix S has a unique positive-definite symmetric square root S1/2. We can again use the "cyclic property" of the trace to write
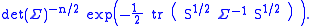
Let B = S1/2 Σ −1 S1/2. Then the expression above becomes
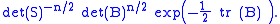
The positive-definite matrix B can be diagonalized, and then the problem of finding the value of B that maximizes
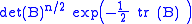
reduces to the problem of finding the values of the diagonal entries λ1, ..., λp that maximize
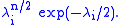
This is just a calculus problem and we get λi = n, so that B = n Ip, i.e., n times the p×p identity matrix.
Concluding steps
Finally we get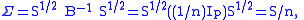i.e., the p×p "sample covariance matrix"
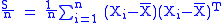
is the maximum-likelihood estimator of the "population covariance matrix" Σ. At this point we are using a capital X rather than a lower-case x because we are thinking of it "as an estimator rather than as an estimate", i.e., as something random whose probability distribution we could profit by knowing. The random matrix S can be shown to have a Wishart distribution with n − 1 degrees of freedom. That is:
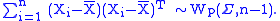
Alternative derivation
An alternative derivation of the maximum likelihood estimator can be performed via matrix calculusMatrix calculus
In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices, where it defines the matrix derivative. This notation was to describe systems of differential equations, and taking derivatives of matrix-valued functions with respect...
formulae (see also differential of a determinant and differential of the inverse matrix). It also verifies the aforementioned fact about the maximum likelihood estimate of the mean. Re-write the likelihood in the log form using the trace trick:
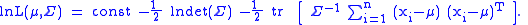
The differential of this log-likelihood is
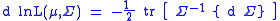
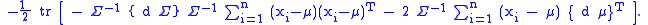
It naturally breaks down into the part related to the estimation of the mean, and to the part related to the estimation of the variance. The first order condition for maximum,
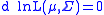, is satisfied when the terms multiplying and are identically zero. Assuming (the maximum likelihood estimate of) is non-singular, the first order condition for the estimate of the mean vector is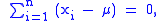which leads to the maximum likelihood estimator
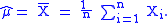
This lets us simplify
as defined above. Then the terms involving in 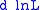can be combined as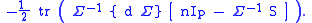The first order condition
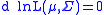will hold when the term in the square bracket is (matrix-valued) zero. Pre-multiplying the latter by and dividing by gives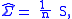which of course coincides with the canonical derivation given earlier.
Dwyer points out that decomposition into two terms such as appears above is "unnecessary" and derives the estimator in two lines of working. Note that it may be not trivial to show that such derived estimator is the unique global maximizer for likelihood function.
Intrinsic expectation
Given a sampleSample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
of n independent observations x1,..., xn of a p-dimensional zero-mean Gaussian random variable X with covariance R, the maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of R is given by
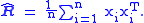
The parameter R belongs to the set of positive-definite matrices
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, which is a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, not a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, hence the usual vector-space notions of expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, i.e. "E[R^]", and estimator bias must be generalized to manifolds to make sense of the problem of covariance matrix estimation. This can be done by defining the expectation of an manifold-valued estimator R^ with respect to the manifold-valued point R as
where
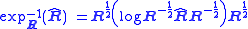
are the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
and inverse exponential map, respectively, "exp" and "log" denote the ordinary matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
and matrix logarithm, and E[·] is the ordinary expectation operator defined on a vector space, in this case the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of the manifold.
Bias of the sample covariance matrix
The intrinsic bias vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
of the SCM estimator R^ is defined to be
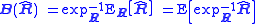
The intrinsic estimator bias is then given by
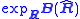.For complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Gaussian random variables, this bias vector field can be shown to equal
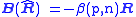
where
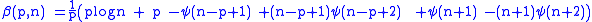
and ψ(·) is the digamma function. The intrinsic bias of the sample covariance matrix equals
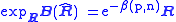
and the SCM is asymptotically unbiased as n → ∞.
Similarly, the intrinsic inefficiency
Efficiency (statistics)
In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
of the sample covariance matrix depends upon the Riemannian curvature of the space of positive-define matrices.
Shrinkage estimation
If the sample size n is small and the number of considered variables p is large, the above empirical estimators of covariance and correlation are very unstable. Specifically, it is possible to furnish estimators that improve considerably upon the maximum likelihood estimate in terms of mean squared error. Moreover, for n < p, the empirical estimate of the covariance matrix becomes singular, i.e. it cannot be inverted to compute the precision matrix.As an alternative, many methods have been suggested to improve the estimation of the covariance matrix. All of these approaches rely on the concept of shrinkage. This is implicit in Bayesian methods, in penalized maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
methods, and explicit in the Stein-type shrinkage approach.
A simple version of a shrinkage estimator of the covariance matrix is constructed as follows. One considers a convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of the empirical estimator with some suitable chosen target, e.g., the diagonal matrix. Subsequently, the mixing parameter
is selected to maximize the expected accuracy of the shrunken estimator. This can be done by cross-validation, or by using an analytic estimate of the shrinkage intensity. The resulting regularized estimator can be shown to outperform the maximum likelihood estimator for small samples. For large samples, the shrinkage intensity will reduce to zero, hence in
this case the shrinkage estimator will be identical to the empirical estimator. Apart from increased efficiency the shrinkage estimate has the additional advantage that it is always positive definite and well conditioned.
A review on this topic is given, e.g., in Schäfer and Strimmer 2005.
A covariance shrinkage estimator is implemented in the R package "corpcor".