Cross-cap
Encyclopedia
In mathematics
, a cross-cap is a two-dimensional surface that is a model of a Möbius strip
with a single self intersection. This self intersection precludes the cross-cap from being topologically equivalent (i.e., homeomorphic) to a Möbius strip
. The term ‘cross-cap’, however, often implies that the surface has been deformed so that its boundary is an ordinary circle.
A cross-cap that has been closed up by gluing a disc to its boundary is an immersion of the real projective plane
.
Two cross-caps glued together at their boundaries form a Klein bottle
.
An important theorem of topology
, the classification theorem for surfaces, states that all two-dimensional compact manifold
s without boundary
are homeomorphic to spheres with some number of ‘handles’ and at most two cross-caps.
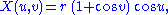
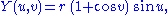
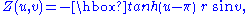
where both u and v range from 0 to 2π.
These equations are similar to those of a torus
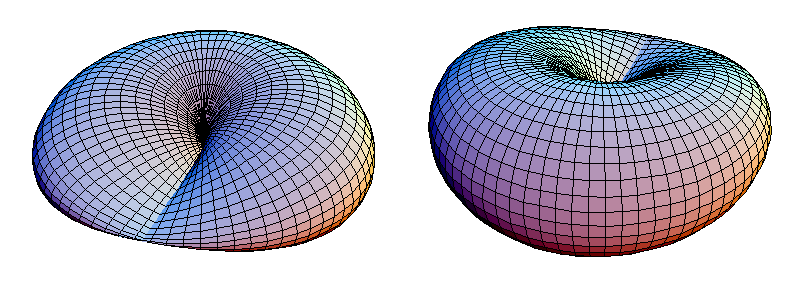
. Figure 1 shows a closed cross-capped disk.
A cross-capped disk has a plane of symmetry which passes through its line segment of double points. In Figure 1 the cross-capped disk is seen from above its plane of symmetry z = 0, but it would look the same if seen from below.
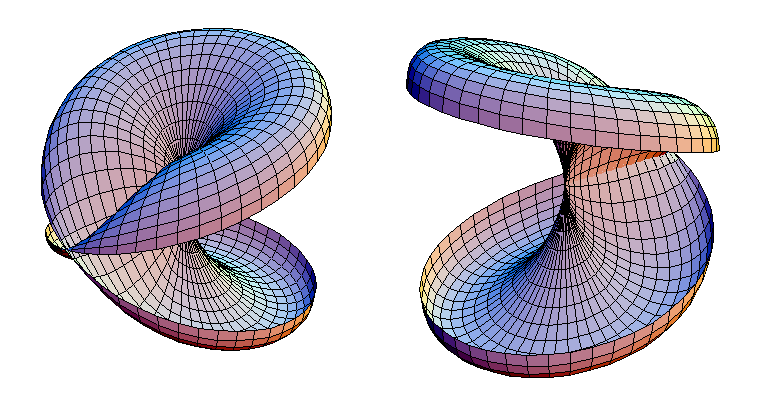
A cross-capped disk can be sliced open along its plane of symmetry, while making sure not to cut along any of its double points. The result is shown in Figure 2.
Once this exception is made, it will be seen that the sliced cross-capped disk is homeomorphic
to a self-intersecting disk, as shown in Figure 3.
The self-intersecting disk is homeomorphic to an ordinary disk. The parametric equations of the self-intersecting disk are: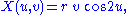
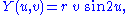
where u ranges from 0 to 2π and v ranges from 0 to 1.
Projecting the self-intersecting disk onto the plane of symmetry (z = 0 in the parametrization given earlier) which passes only through the double points, the result is an ordinary disk which repeats itself (doubles up on itself).
The plane z = 0 cuts the self-intersecting disk into a pair of disks which are mirror reflection
s of each other. The disks have centers at the origin
.
Now consider the rims of the disks (with v = 1). The points on the rim of the self-intersecting disk come in pairs which are reflections of each other with respect to the plane z = 0.
A cross-capped disk is formed by identifying these pairs of points, making them equivalent to each other. This means that a point with parameters (u,1) and coordinates
is identified with the point (u + π,1) whose coordinates are 
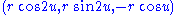. But this means that pairs of opposite points on the rim of the (equivalent) ordinary disk are identified with each other; this is how a real projective plane is formed out of a disk. Therefore the surface shown in Figure 1 (cross-cap with disk) is topologically equivalent to the real projective plane RP2.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a cross-cap is a two-dimensional surface that is a model of a Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
with a single self intersection. This self intersection precludes the cross-cap from being topologically equivalent (i.e., homeomorphic) to a Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
. The term ‘cross-cap’, however, often implies that the surface has been deformed so that its boundary is an ordinary circle.
A cross-cap that has been closed up by gluing a disc to its boundary is an immersion of the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
.
Two cross-caps glued together at their boundaries form a Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
.
An important theorem of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the classification theorem for surfaces, states that all two-dimensional compact manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s without boundary
are homeomorphic to spheres with some number of ‘handles’ and at most two cross-caps.
Cross-capped disk model of the real projective plane
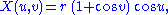
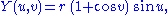
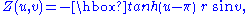
The term cross-cap is also inaccurately used to refer to the closed surface obtained by gluing a disk to a cross-cap. This is, in fact, a cross-cap glued to a disk. This surface can be represented parametrically by the following equations:where both u and v range from 0 to 2π.
These equations are similar to those of a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. Figure 1 shows a closed cross-capped disk.
 |
|
A cross-capped disk has a plane of symmetry which passes through its line segment of double points. In Figure 1 the cross-capped disk is seen from above its plane of symmetry z = 0, but it would look the same if seen from below.
A cross-capped disk can be sliced open along its plane of symmetry, while making sure not to cut along any of its double points. The result is shown in Figure 2.
 |
|
Once this exception is made, it will be seen that the sliced cross-capped disk is homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to a self-intersecting disk, as shown in Figure 3.
 |
|
The self-intersecting disk is homeomorphic to an ordinary disk. The parametric equations of the self-intersecting disk are:
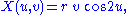
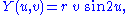
where u ranges from 0 to 2π and v ranges from 0 to 1.
Projecting the self-intersecting disk onto the plane of symmetry (z = 0 in the parametrization given earlier) which passes only through the double points, the result is an ordinary disk which repeats itself (doubles up on itself).
The plane z = 0 cuts the self-intersecting disk into a pair of disks which are mirror reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s of each other. The disks have centers at the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
.
Now consider the rims of the disks (with v = 1). The points on the rim of the self-intersecting disk come in pairs which are reflections of each other with respect to the plane z = 0.
A cross-capped disk is formed by identifying these pairs of points, making them equivalent to each other. This means that a point with parameters (u,1) and coordinates
is identified with the point (u + π,1) whose coordinates are 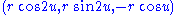. But this means that pairs of opposite points on the rim of the (equivalent) ordinary disk are identified with each other; this is how a real projective plane is formed out of a disk. Therefore the surface shown in Figure 1 (cross-cap with disk) is topologically equivalent to the real projective plane RP2.