
Conference graph
Encyclopedia
In the mathematical
area of graph theory
, a conference graph is a strongly regular graph
with parameters v, and It is the graph associated with a symmetric conference matrix
, and consequently its order v must be 1 (modulo 4) and a sum of two squares.
Conference graphs are known to exist for all small values of v allowed by the restrictions, e.g., v = 5, 9, 13, 17, 25, 29, and (the Paley graph
s) for all prime powers congruent to 1 (modulo 4). However, there are many values of v that are allowed, for which the existence of a conference graph is unknown.
The eigenvalues of a conference graph need not be integers, unlike those of other strongly regular graphs. If the graph is connected, the eigenvalues are k with multiplicity 1, and two other eigenvalues,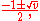
each with multiplicity
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
area of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a conference graph is a strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
with parameters v, and It is the graph associated with a symmetric conference matrix
Conference matrix
In mathematics, a conference matrix is a square matrix C with 0 on the diagonal and +1 and −1 off the diagonal, such that CTC is a multiple of the identity matrix I...
, and consequently its order v must be 1 (modulo 4) and a sum of two squares.
Conference graphs are known to exist for all small values of v allowed by the restrictions, e.g., v = 5, 9, 13, 17, 25, 29, and (the Paley graph
Paley graph
In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...
s) for all prime powers congruent to 1 (modulo 4). However, there are many values of v that are allowed, for which the existence of a conference graph is unknown.
The eigenvalues of a conference graph need not be integers, unlike those of other strongly regular graphs. If the graph is connected, the eigenvalues are k with multiplicity 1, and two other eigenvalues,
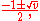
each with multiplicity

