
Shrikhande graph
Encyclopedia
In the mathematical
field of graph theory
, the Shrikhande graph is a named graph
discovered by S. S. Shrikhande
in 1959. It is a strongly regular graph
with 16 vertices
and 48 edges, with each vertex having a degree
of 6.
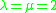 , this equality implying that the graph is associated with a symmetric
, this equality implying that the graph is associated with a symmetric
BIBD. It shares these parameters with a different graph, the 4×4 rook's graph
.
The Shrikhande graph is locally hexagonal
; that is, the neighbors of each vertex form a cycle
of six vertices. As with any locally cyclic graph, the Shrikhande graph is the 1-skeleton
of a Whitney triangulation
of some surface; in the case of the Shrikhande graph, this surface is a torus
in which each vertex is surrounded by six triangles. Thus, the Shrikhande graph is a toroidal graph
. The dual of this embedding is the Dyck graph
, a cubic symmetric graph.
The Shrikhande graph is not a distance-transitive graph
. It is the smallest distance-regular graph that is not distance-transitive.
The automorphism group
of the Shrikhande graph is of order 192. It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Shrikhande graph is a symmetric graph
.
The characteristic polynomial
of the Shrikhande graph is :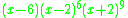 . Therefore the Shrikhande graph is an integral graph
. Therefore the Shrikhande graph is an integral graph
: its spectrum
consists entirely of integers.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Shrikhande graph is a named graph
Gallery of named graphs
Some of the finite structures considered in graph theory have names, sometimes inspired by the graph's topology, and sometimes after their discoverer. A famous example is the Petersen graph, a concrete graph on 10 vertices that appears as a minimal example or counterexample in many different...
discovered by S. S. Shrikhande
S. S. Shrikhande
Sharadchandra Shankar Shrikhande is an Indian mathematician with distinguished and well-recognized achievements in combinatorial mathematics. He is notable for his breakthrough work along with R. C. Bose and E. T...
in 1959. It is a strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
with 16 vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
and 48 edges, with each vertex having a degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
of 6.
Properties
In the Shrikhande graph, any two vertices I and J have two distinct neighbors in common (excluding the two vertices I and J themselves), which holds true whether or not I is adjacent to J. In other words, its parameters for being strongly regular are: {16,6,2,2}, with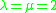 , this equality implying that the graph is associated with a symmetric
, this equality implying that the graph is associated with a symmetricSymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
BIBD. It shares these parameters with a different graph, the 4×4 rook's graph
Rook's graph
In graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard: each vertex represents a square on a chessboard and each edge represents a legal move...
.
The Shrikhande graph is locally hexagonal
Neighbourhood (graph theory)
In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the induced subgraph of G consisting of all vertices adjacent to v and all edges connecting two such vertices. For example, the image shows a...
; that is, the neighbors of each vertex form a cycle
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
of six vertices. As with any locally cyclic graph, the Shrikhande graph is the 1-skeleton
N-skeleton
In mathematics, particularly in algebraic topology, the n-skeleton of a topological space X presented as a simplicial complex refers to the subspace Xn that is the union of the simplices of X of dimensions m ≤ n...
of a Whitney triangulation
Triangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
of some surface; in the case of the Shrikhande graph, this surface is a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
in which each vertex is surrounded by six triangles. Thus, the Shrikhande graph is a toroidal graph
Toroidal graph
In mathematics, a graph G is toroidal if it can be embedded on the torus. In other words, the graph's vertices can be placed on a torus such that no edges cross...
. The dual of this embedding is the Dyck graph
Dyck graph
In the mathematical field of graph theory, the Dyck graph is a 3-regular graph with 32 vertices and 48 edges, named after Walther von Dyck.It is Hamiltonian with 120 distinct Hamiltonian cycles. It has chromatic number 2, chromatic index 3, radius 5, diameter 5 and girth 6...
, a cubic symmetric graph.
The Shrikhande graph is not a distance-transitive graph
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
. It is the smallest distance-regular graph that is not distance-transitive.
The automorphism group
Graph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
of the Shrikhande graph is of order 192. It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Shrikhande graph is a symmetric graph
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Shrikhande graph is :
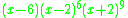 . Therefore the Shrikhande graph is an integral graph
. Therefore the Shrikhande graph is an integral graphIntegral graph
In the mathematical field of graph theory, an integral graph is a graph whose spectrum consists entirely of integers. In other words, a graphs is an integral graph if all the eigenvalues of its characteristic polynomial are integers....
: its spectrum
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
consists entirely of integers.
External links
- The Shrikhande Graph, Peter CameronPeter Cameron (mathematician)Peter Jephson Cameron is an Australian mathematician who works ingroup theory, combinatorics, coding theory, and model theory. He is currently Professor of Mathematics at Queen Mary, University of London....
, August 2010.

